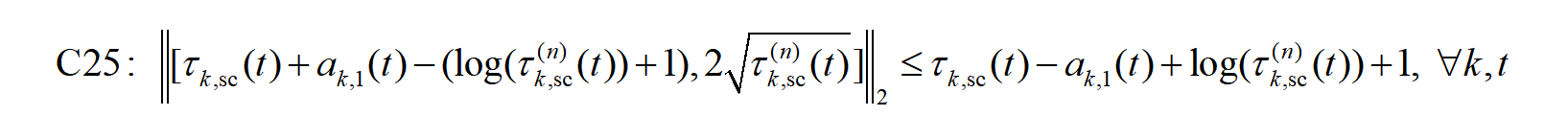Help! After adding a second-order cone constraint, the original problem becomes unfeasible

FastGraduate · November 21, 2024, 3:12am

Hello, everyone! I’m having the following problem: After adding a second-order cone constraint, the original problem becomes unfeasible. My code and original issue are below.

clear all;

S = 2;
C = 8;
U = 30;
T = 5; 
Ntx = 2;  
Nty = 2;
Nt = Ntx * Nty;  
% 
C_pos = [175.63, 106.87; 136.30, 43.52; 45.78, 130.01; 112.98, 160.91; 203.56, 61.04; 211.69, 102.28; 199.17, 156.30; 250.84, 82.47];

S_height = 2000;  % km

s1_pos = [106, 95]; 
offset = 2; 
S1_pos = zeros(2, T);  
S1_pos(:, 1) = s1_pos';
for t = 2:T
    S1_pos(:, t) = S1_pos(:, t-1) + offset;
end

s2_pos = [106, 95];  
S2_pos = zeros(2, T);  
S2_pos(:, 1) = s2_pos';
for t = 2:T
    S2_pos(:, t) = S2_pos(:, t-1) + offset;
end


C1_user_pos = [
    171.2722264020125, 109.00801070894408;
    170.78417466125165, 108.35008091794222;
    173.67173899833338, 108.37931961155354;
    174.57454953552102, 110.32493726720683
    ];
C2_user_pos = [
    139.40651298082275, 38.67803930763517;
    136.32860551422957, 42.16289711432755;
    137.82744015490138, 49.40391946858323
    ];
C3_user_pos = [
    50.220941592900196, 127.20160520535724;
    44.84591869552337, 131.65090563826476;
    44.000564580961424, 129.4559770874314;
    43.8824784449596, 125.8989690461711
    ];
C4_user_pos = [
    113.08499873947316, 158.80371594827875;
    111.5920437225002, 164.10212705332233;
    116.41936814395419, 163.36229468704227;
    116.19780560454484, 160.09214237182525
    ];
C5_user_pos = [
    205.220426703268, 65.84596511048743;
    202.8614646798177, 60.19082268959938;
    203.8759909567894, 65.23328051265051;
    203.66097558905423, 60.33373793784346;
    ];
C6_user_pos = [
    216.05019293657938, 105.26821222254914;
    209.9937625083976, 102.80067798301602;
    212.47281462868258, 101.69097593870022
    ];
C7_user_pos = [
    198.13023757449002, 156.0800008435594;
    192.6303832555794, 157.87173209488702;
    193.86260478222596, 150.9149777689437;
    199.26240273494048, 157.46780698355275
    ];
C8_user_pos = [
    249.9419764502806, 86.23344713333803;
    253.8960558978885, 85.18919781572083;
    255.8605921815085, 81.64237655577355;
    249.118031669222, 82.20905242308542
    ];

user_positions = {
    C1_user_pos, C2_user_pos, C3_user_pos, C4_user_pos, ...
    C5_user_pos, C6_user_pos, C7_user_pos, C8_user_pos
};
all_user_positions = vertcat(user_positions{:});  
user_counts_per_cluster = [4, 3, 4, 4, 4, 3, 4, 4];  

cluster_user_indices = cell(1, length(user_counts_per_cluster));

start_index = 1;


for c = 1:length(user_counts_per_cluster)
    end_index = start_index + user_counts_per_cluster(c) - 1;
    cluster_user_indices{c} = start_index:end_index;
    start_index = end_index + 1;
end

disp(cluster_user_indices)

d = zeros(S, U, T);  
for m = 1:S
    for u = 1:size(all_user_positions, 1)  
        for t = 1:T
           
            if m == 1
                satellite_pos = S1_pos(:, t); 
            else
                satellite_pos = S2_pos(:, t);  
            end
            

            user_pos = all_user_positions(u, :);  
            

            distance = sqrt((satellite_pos(1) - user_pos(1))^2 + ...
                            (satellite_pos(2) - user_pos(2))^2 + ...
                            (S_height - 0)^2); 
            
            d(m, u, t) = distance;
        end
    end
end

disp(d)  % 2000

c = 3e8;           
f_c = 2e9;         
g_t = 10;            
g_r = 5;            

gain = zeros(S, U, T);  
for m = 1:S
    for u = 1:size(all_user_positions, 1) 
        for t = 1:T
            delta = abs(randn);  
            dist = d(m, u, t); 
            gain(m, u, t) = delta * sqrt(g_t * g_r * (c / (4 * pi * f_c * dist * 1e3))^2);
        end
    end
end
disp("gain")
disp(gain)  % 1e-5

% h = zeros(S, Nt, U, T);  
h = zeros(Nt, S, U, T);


doppler_shift = 100;   
time_delay = 1e-6;    


theta_x = 0.1;      
theta_y = 0.2;        


array_response = @(N, theta) 1/sqrt(N) * exp(-1j * pi * theta * (0:N-1)).';

v_x = array_response(Ntx, theta_x);
v_y = array_response(Nty, theta_y);

v_k = kron(v_x, v_y);  % v_k的维度为 Nt^2 x 1

for m = 1:S
    for u = 1:size(all_user_positions, 1)
        for t = 1:T
            % fprintf('m = %d, i = %d, n = %d, t = %d\n', m, i, n, t);

            g_m_i_n_t = gain(m, u, t);

            phase_factor = exp(1j * 2 * pi * (doppler_shift * t - f_c * time_delay));


            h(:, m, u, t) = g_m_i_n_t * phase_factor * v_k * 1e7;
        end
    end
end

h1 = h(:, 1, :, :);  
h2 = h(:, 2, :, :);
H1 = zeros(Nt, Nt, T);  
H2 = zeros(Nt, Nt, T);  
for t = 1:T
    h1_t = h1(:, :, t);        
    h2_t = h2(:, :, t);        
    
    H1(:, :, t) = h1_t * h1_t';  
    H2(:, :, t) = h2_t * h2_t';  
end

disp('H1:');
disp(H1)  % 1e-8
disp('H2:');
disp(H2)

wide_beam_cover_matrix = [
    [1, 1, 1, 1, 0, 0, 0, 0];
    [1, 0, 0, 0, 1, 1, 1, 1]
];  
wideBeamCover = zeros(S, C, T);

for t = 1:T
    wideBeamCover(:, :, t) = wide_beam_cover_matrix;
end

spotBeamCover = zeros(S, C, T);

for t = 1:T
    for s = 1:S
      
        available_clusters = find(wideBeamCover(s, :, t) == 1);
        
      
        if length(available_clusters) <= 3
            selected_clusters = available_clusters;
        else
            selected_clusters = randsample(available_clusters, 3);
        end
        
       
        spotBeamCover(s, selected_clusters, t) = 1;
    end
end


total_users_covered_by_spotbeam = zeros(S, T);

for s = 1:S
    for t = 1:T
      
        covered_clusters = find(spotBeamCover(s, :, t) == 1);        
      
        total_users_covered = sum(user_counts_per_cluster(covered_clusters));        
       
        total_users_covered_by_spotbeam(s, t) = total_users_covered; 
    end
end


k = 1.38e-23; 
noise_T = 290;      
B = 20e6;      
F = 10;     

P_noise = k * noise_T * B * F * 1e11;  

disp(P_noise)  % 1e-13
P_beam = 10 * ones(Nt, 1);

disp(P_beam)

Asc2_prev = rand(U, T); 
% Asc2_prev = ones(U, T);
Bc2_prev = rand(U, T);
Cn2_prev = rand(U, T);
TAOsc_prev_external = 1000 + (20 - 10) * rand(U, T);
TAOc_prev = rand(U, T);
TAOn_prev = rand(U, T);




total_users_per_timeslot = zeros(1, T);

for t = 1:T
    
    scheduled_clusters = false(1, C);
  
    for s = 1:S
       
        scheduled_clusters = scheduled_clusters | (spotBeamCover(s, :, t) > 0);  
    end
    
  
    unique_users = [];
    
    for c = 1:C
        if scheduled_clusters(c) 
           
            cluster_users = cluster_user_indices{c};
            
     
            unique_users = union(unique_users, cluster_users);
        end
    end

    total_users_per_timeslot(t) = length(unique_users);
end 

lambda_max_Usc = zeros(S, T);   
v_max_Usc = ones(Nt, S, T) / sqrt(Nt);        

lambda_max_Uc = zeros(S, C, T);     
v_max_Uc = ones(Nt, S, C, T) / sqrt(Nt);      

lambda_max_Un = zeros(S, U, T);     
v_max_Un = ones(Nt, S, U, T) / sqrt(Nt);     

% cvx_solver Mosek
for iter = 1:3
    % TAOsc_prev_external = max(TAOsc_prev_external, 1e-6);
    cvx_begin sdp
        variable Usc(Nt, Nt, S, T) semidefinite;  
        variable Uc(Nt, Nt, S, C, T) semidefinite;  
        variable Un(Nt, Nt, S, U, T) semidefinite;
        % variable Qsc(U, T); 
        variable Rsc(T);   
        % variable Qc(U, T); 
        variable Rc(C, T);  
        variable Qn(U, T);
        variable Asc1(U, T);  
        variable Asc2(U, T);
        variable Bc1(U, T);
        variable Bc2(U, T);
        variable Cn1(U, T);
        variable Cn2(U, T);
        variable TAOsc(U, T);
        variable TAOc(U, T);
        variable TAOn(U, T);
        expression O;  
        % expression H(Nt, Nt);
        expression Qsc(U, T);
        expression Qc(U, T);
        expression P_total(Nt, S, T);
        expression A2LHS(U, T);
        expression A1RHS(U, T);
        expression B2LHS(U, T);
        expression B1RHS(U, T);
        expression C2LHS(U, T);
        expression C1RHS(U, T);
        expression TAOsc_prev(U, T);
        expression value;

        TAOsc_prev = TAOsc_prev_external;
        
        

        for t = 1:T  % O
            O = 0;
            O = O + Rsc(t) / total_users_per_timeslot(t);
        end



        for t = 1:T  % C12
            for s = 1:S  
                P_total(:, s, t) = 0;
                P_total(:, s, t) = P_total(:, s, t) + diag(Usc(:,:,s,t));
            end
        end
        

        f = 0;
        for s = 1:S
            for t = 1:T
                f = f + trace(Usc(:, :, s, t)) - v_max_Usc(:, s, t)' * Usc(:, :, s, t) * v_max_Usc(:, s, t);
            end
        end
        
        
        maximize(O - f);
        
    
        subject to

            for t = 1:T
                for s = 1:S
                    for c = 1:C
                        if spotBeamCover(s, c, t) == 1
                            user_indices = cluster_user_indices{c};
                            for u = user_indices
                                Rsc(t) <= Qsc(u, t);
                            end
                        end
                    end
                end
            end
    
            for t = 1:T
                for c = 1:C
                    user_indices = cluster_user_indices{c};
                    for u = user_indices
                        Rc(c, t) <= Qc(u, t);
                    end
                end
            end
    
            for t = 1:T
                Rsc(t) >= 1e-5;
            end
    
            for t = 1:T
                for c = 1:C
                    Rc(c, t) >= 1e-5;
                end
            end
    
            for t = 1:T
                for u = 1:U
                    Qn(u, t) >= 1e-5;
                end
            end

            for t = 1:T  % C12
                for s = 1:S
                    P_total(:, s, t) <= P_beam;
                end
            end
            
            for t = 1:T   % C1
                for u = 1:U
                    Asc1(u, t) - Asc2(u, t) >= Qsc(u, t); 
                end
            end

            for t = 1:T  % C13左侧
                for s = 1:S
                    if s == 1
                        H = H1(:, :, t);
                    else
                        H = H2(:, :, t);
                    end
                 
                    for c = 1:C
                        if spotBeamCover(s, c, t) == 1
                            A2LHS(u, t) = A2LHS(u, t) + trace(H * Uc(:, :, s, c, t));
                            for u = 1:U
                                if ismember(u, cluster_user_indices{c})
                                    A2LHS(u, t) = A2LHS(u, t) + trace(H * Un(:, :, s, u, t));
                                end
                            end
                        end
                    end
                    A2LHS(u, t) = A2LHS(u, t) + P_noise;
                    % ------
                end
            end

            for t = 1:T 
                for s = 1:S
                    if s == 1
                        H = H1(:, :, t);
                    else
                        H = H2(:, :, t);
                    end

                    A1RHS(u, t) = A2LHS(u, t) + trace(H * Usc(:, :, s, t));
                end
            end

            for t = 1:T  % C13
                for u = 1:U
                    value = exp(Asc2_prev(u, t));
                    % Asc2_prev(u, t) + rel_entr(1, value) <= 0;
                    A2LHS(u, t) <= value * (Asc2(u, t) - Asc2_prev(u, t) + 1);
                end
            end
            
            for t = 1:T  % C16
                for u = 1:U
                    TAOsc(u, t) <= A1RHS(u, t);
                    % TAOsc(u, t) >= 0;
                end
            end
            
            for t = 1:T  %  C25
                for u = 1:U

                    norm([TAOsc(u, t) + Asc1(u, t) - (log(TAOsc_prev(u, t)) + 1), 2 * sqrt(TAOsc_prev(u, t))], 2) ...
                        <= TAOsc(u, t) - Asc1(u, t) + log(TAOsc_prev(u, t)) + 1;  
                      
                end
            end
    cvx_end

    Asc2_prev = Asc2;

    for s = 1:S
        for t = 1:T
           
            P = Usc(:, :, s, t);
            disp("P")
            disp(P)
            [V, D] = eig(double(P));
            [lambda_max, idx] = max(diag(D));
            v_max = V(:, idx);
            v_max = v_max / norm(v_max); % 归一化
            lambda_max_Usc(s, t) = lambda_max;
            v_max_Usc(:, s, t) = v_max;
        end
    end
end

original issue:
sorry, i’m new to. I can only post one picture.

The output of cvx solver as below:

ljTest
各簇用户索引
{[1 2 3 4]} {[5 6 7]} {[8 9 10 11]} {[12 13 14 15]} {[16 17 18 19]} {[20 21 22]} {[23 24 25 26]} {[27 28 29 30]}

距离

(:,:,1) =

1.0e+03 *

列 1 至 13

2.0011    2.0011    2.0012    2.0012    2.0011    2.0009    2.0008    2.0010    2.0013    2.0013    2.0012    2.0010    2.0012
2.0011    2.0011    2.0012    2.0012    2.0011    2.0009    2.0008    2.0010    2.0013    2.0013    2.0012    2.0010    2.0012

列 14 至 26

2.0012    2.0011    2.0027    2.0026    2.0026    2.0027    2.0031    2.0027    2.0028    2.0031    2.0029    2.0027    2.0031
2.0012    2.0011    2.0027    2.0026    2.0026    2.0027    2.0031    2.0027    2.0028    2.0031    2.0029    2.0027    2.0031

列 27 至 30

2.0052    2.0055    2.0057    2.0052
2.0052    2.0055    2.0057    2.0052

(:,:,2) =

1.0e+03 *

列 1 至 13

2.0010    2.0010    2.0011    2.0012    2.0011    2.0010    2.0008    2.0011    2.0013    2.0013    2.0012    2.0010    2.0011
2.0010    2.0010    2.0011    2.0012    2.0011    2.0010    2.0008    2.0011    2.0013    2.0013    2.0012    2.0010    2.0011

列 14 至 26

2.0011    2.0010    2.0026    2.0026    2.0025    2.0026    2.0029    2.0026    2.0027    2.0029    2.0027    2.0026    2.0030
2.0011    2.0010    2.0026    2.0026    2.0025    2.0026    2.0029    2.0026    2.0027    2.0029    2.0027    2.0026    2.0030

列 27 至 30

2.0051    2.0053    2.0055    2.0050
2.0051    2.0053    2.0055    2.0050

(:,:,3) =

1.0e+03 *

列 1 至 13

2.0010    2.0009    2.0010    2.0011    2.0011    2.0010    2.0008    2.0011    2.0013    2.0013    2.0013    2.0009    2.0011
2.0010    2.0009    2.0010    2.0011    2.0011    2.0010    2.0008    2.0011    2.0013    2.0013    2.0013    2.0009    2.0011

列 14 至 26

2.0010    2.0009    2.0025    2.0025    2.0025    2.0026    2.0028    2.0025    2.0026    2.0028    2.0026    2.0024    2.0028
2.0010    2.0009    2.0025    2.0025    2.0025    2.0026    2.0028    2.0025    2.0026    2.0028    2.0026    2.0024    2.0028

列 27 至 30

2.0049    2.0052    2.0054    2.0049
2.0049    2.0052    2.0054    2.0049

(:,:,4) =

1.0e+03 *

列 1 至 13

2.0009    2.0009    2.0010    2.0010    2.0012    2.0010    2.0008    2.0011    2.0014    2.0014    2.0013    2.0008    2.0010
2.0009    2.0009    2.0010    2.0010    2.0012    2.0010    2.0008    2.0011    2.0014    2.0014    2.0013    2.0008    2.0010

列 14 至 26

2.0010    2.0009    2.0025    2.0025    2.0024    2.0025    2.0027    2.0024    2.0025    2.0026    2.0024    2.0023    2.0027
2.0010    2.0009    2.0025    2.0025    2.0024    2.0025    2.0027    2.0024    2.0025    2.0026    2.0024    2.0023    2.0027

列 27 至 30

2.0048    2.0051    2.0053    2.0048
2.0048    2.0051    2.0053    2.0048

(:,:,5) =

1.0e+03 *

列 1 至 13

2.0008    2.0008    2.0009    2.0009    2.0012    2.0010    2.0009    2.0012    2.0014    2.0014    2.0014    2.0008    2.0009
2.0008    2.0008    2.0009    2.0009    2.0012    2.0010    2.0009    2.0012    2.0014    2.0014    2.0014    2.0008    2.0009

列 14 至 26

2.0009    2.0008    2.0024    2.0024    2.0024    2.0025    2.0026    2.0023    2.0024    2.0025    2.0023    2.0022    2.0026
2.0009    2.0008    2.0024    2.0024    2.0024    2.0025    2.0026    2.0023    2.0024    2.0025    2.0023    2.0022    2.0026

列 27 至 30

2.0047    2.0050    2.0051    2.0047
2.0047    2.0050    2.0051    2.0047

gain

(:,:,1) =

1.0e-07 *

列 1 至 13

0.4832    0.4636    0.3352    0.8041    0.3886    0.1264    0.0020    0.2000    0.3531    0.0617    0.3165    0.3663    0.1776
0.0250    0.3652    0.1617    0.1210    0.2288    0.4283    0.0948    0.3266    0.0467    0.3054    0.2902    0.3457    0.2305

列 14 至 26

0.4538    0.1754    0.2422    0.0166    0.1560    0.4247    0.2759    0.2748    0.7729    0.8683    0.2686    0.4999    0.9368
0.1330    0.3269    0.1522    0.4181    0.5436    0.5103    0.2075    0.0811    0.3165    0.1324    0.1309    0.1839    0.4835

列 27 至 30

0.5068    0.2555    0.2304    0.5054
0.3179    0.1439    0.4256    0.0716

(:,:,2) =

1.0e-06 *

列 1 至 13

0.0046    0.0039    0.0047    0.0773    0.0013    0.0399    0.0065    0.0694    0.0005    0.1093    0.0132    0.0090    0.0298
0.0722    0.0079    0.0174    0.0234    0.0475    0.0332    0.0274    0.0224    0.0336    0.0824    0.0263    0.0260    0.0248

列 14 至 26

0.0354    0.0831    0.0053    0.0576    0.0031    0.0293    0.0835    0.0047    0.0770    0.0376    0.0717    0.0556    0.0199
0.0187    0.0016    0.0084    0.1070    0.0557    0.0103    0.1005    0.0330    0.0485    0.0139    0.0188    0.0100    0.0650

列 27 至 30

0.0259    0.0307    0.0101    0.0389
0.0062    0.0270    0.0444    0.0019

(:,:,3) =

1.0e-06 *

列 1 至 13

0.0388    0.0168    0.0391    0.0184    0.0106    0.0160    0.0873    0.0020    0.0208    0.0171    0.0144    0.0054    0.0561
0.0630    0.0140    0.1038    0.0057    0.0022    0.0074    0.0136    0.0137    0.0504    0.0334    0.0419    0.0805    0.0011

列 14 至 26

0.0223    0.0135    0.0519    0.0297    0.0092    0.0606    0.0461    0.0100    0.0200    0.0240    0.0874    0.0317    0.0174
0.0196    0.0907    0.0040    0.0596    0.0411    0.0395    0.0161    0.0690    0.0049    0.0153    0.0928    0.0503    0.0364

列 27 至 30

0.0253    0.0272    0.0725    0.0680
0.0187    0.0009    0.0974    0.0447

(:,:,4) =

1.0e-06 *

列 1 至 13

0.0013    0.0644    0.0247    0.1020    0.0543    0.0310    0.0018    0.0686    0.0204    0.0171    0.0256    0.0269    0.0125
0.0048    0.0183    0.0469    0.0140    0.0495    0.0043    0.0623    0.0655    0.0219    0.0180    0.0262    0.0056    0.0323

列 14 至 26

0.0258    0.0686    0.0141    0.0423    0.0010    0.0266    0.0490    0.0314    0.0058    0.0607    0.0372    0.0145    0.0371
0.0094    0.0773    0.0217    0.0260    0.0117    0.0322    0.0527    0.0585    0.0206    0.0023    0.0086    0.0097    0.0129

列 27 至 30

0.0693    0.1034    0.1126    0.1260
0.0180    0.0249    0.0558    0.0286

(:,:,5) =

1.0e-06 *

列 1 至 13

0.0263    0.0491    0.0341    0.0279    0.1042    0.0851    0.0008    0.0489    0.0091    0.0051    0.0978    0.0176    0.0238
0.0066    0.0225    0.0593    0.0797    0.0079    0.0030    0.0260    0.0600    0.0260    0.1274    0.0746    0.0387    0.0064

列 14 至 26

0.0160    0.0422    0.0165    0.0784    0.0286    0.0245    0.0751    0.0702    0.0290    0.0138    0.0331    0.0221    0.1348
0.0262    0.0314    0.0616    0.0248    0.0008    0.0438    0.0242    0.0174    0.0308    0.0110    0.0310    0.0163    0.0588

列 27 至 30

0.0089    0.0311    0.0221    0.0700
0.0277    0.0099    0.0450    0.0476

H1:

(:,:,1) =

0.0584 + 0.0000i 0.0472 + 0.0343i 0.0555 + 0.0180i 0.0343 + 0.0472i
0.0472 - 0.0343i 0.0584 + 0.0000i 0.0555 - 0.0180i 0.0555 + 0.0180i
0.0555 - 0.0180i 0.0555 + 0.0180i 0.0584 + 0.0000i 0.0472 + 0.0343i
0.0343 - 0.0472i 0.0555 - 0.0180i 0.0472 - 0.0343i 0.0584 + 0.0000i

(:,:,2) =

0.0537 + 0.0000i 0.0435 + 0.0316i 0.0511 + 0.0166i 0.0316 + 0.0435i
0.0435 - 0.0316i 0.0537 + 0.0000i 0.0511 - 0.0166i 0.0511 + 0.0166i
0.0511 - 0.0166i 0.0511 + 0.0166i 0.0537 + 0.0000i 0.0435 + 0.0316i
0.0316 - 0.0435i 0.0511 - 0.0166i 0.0435 - 0.0316i 0.0537 + 0.0000i

(:,:,3) =

0.0281 + 0.0000i 0.0227 + 0.0165i 0.0267 + 0.0087i 0.0165 + 0.0227i
0.0227 - 0.0165i 0.0281 + 0.0000i 0.0267 - 0.0087i 0.0267 + 0.0087i
0.0267 - 0.0087i 0.0267 + 0.0087i 0.0281 + 0.0000i 0.0227 + 0.0165i
0.0165 - 0.0227i 0.0267 - 0.0087i 0.0227 - 0.0165i 0.0281 + 0.0000i

(:,:,4) =

0.1617 + 0.0000i 0.1308 + 0.0950i 0.1537 + 0.0500i 0.0950 + 0.1308i
0.1308 - 0.0950i 0.1617 + 0.0000i 0.1537 - 0.0500i 0.1537 + 0.0500i
0.1537 - 0.0500i 0.1537 + 0.0500i 0.1617 + 0.0000i 0.1308 + 0.0950i
0.0950 - 0.1308i 0.1537 - 0.0500i 0.1308 - 0.0950i 0.1617 + 0.0000i

(:,:,5) =

0.0377 + 0.0000i 0.0305 + 0.0222i 0.0359 + 0.0117i 0.0222 + 0.0305i
0.0305 - 0.0222i 0.0377 + 0.0000i 0.0359 - 0.0117i 0.0359 + 0.0117i
0.0359 - 0.0117i 0.0359 + 0.0117i 0.0377 + 0.0000i 0.0305 + 0.0222i
0.0222 - 0.0305i 0.0359 - 0.0117i 0.0305 - 0.0222i 0.0377 + 0.0000i

H2:

(:,:,1) =

1.0e-03 *

0.1563 + 0.0000i 0.1265 + 0.0919i 0.1487 + 0.0483i 0.0919 + 0.1265i
0.1265 - 0.0919i 0.1563 + 0.0000i 0.1487 - 0.0483i 0.1487 + 0.0483i
0.1487 - 0.0483i 0.1487 + 0.0483i 0.1563 + 0.0000i 0.1265 + 0.0919i
0.0919 - 0.1265i 0.1487 - 0.0483i 0.1265 - 0.0919i 0.1563 + 0.0000i

(:,:,2) =

0.0333 + 0.0000i 0.0270 + 0.0196i 0.0317 + 0.0103i 0.0196 + 0.0270i
0.0270 - 0.0196i 0.0333 + 0.0000i 0.0317 - 0.0103i 0.0317 + 0.0103i
0.0317 - 0.0103i 0.0317 + 0.0103i 0.0333 + 0.0000i 0.0270 + 0.0196i
0.0196 - 0.0270i 0.0317 - 0.0103i 0.0270 - 0.0196i 0.0333 + 0.0000i

(:,:,3) =

0.0065 + 0.0000i 0.0053 + 0.0038i 0.0062 + 0.0020i 0.0038 + 0.0053i
0.0053 - 0.0038i 0.0065 + 0.0000i 0.0062 - 0.0020i 0.0062 + 0.0020i
0.0062 - 0.0020i 0.0062 + 0.0020i 0.0065 + 0.0000i 0.0053 + 0.0038i
0.0038 - 0.0053i 0.0062 - 0.0020i 0.0053 - 0.0038i 0.0065 + 0.0000i

(:,:,4) =

0.0037 + 0.0000i 0.0030 + 0.0022i 0.0035 + 0.0011i 0.0022 + 0.0030i
0.0030 - 0.0022i 0.0037 + 0.0000i 0.0035 - 0.0011i 0.0035 + 0.0011i
0.0035 - 0.0011i 0.0035 + 0.0011i 0.0037 + 0.0000i 0.0030 + 0.0022i
0.0022 - 0.0030i 0.0035 - 0.0011i 0.0030 - 0.0022i 0.0037 + 0.0000i

(:,:,5) =

0.0131 + 0.0000i 0.0106 + 0.0077i 0.0125 + 0.0040i 0.0077 + 0.0106i
0.0106 - 0.0077i 0.0131 + 0.0000i 0.0125 - 0.0040i 0.0125 + 0.0040i
0.0125 - 0.0040i 0.0125 + 0.0040i 0.0131 + 0.0000i 0.0106 + 0.0077i
0.0077 - 0.0106i 0.0125 - 0.0040i 0.0106 - 0.0077i 0.0131 + 0.0000i

噪声功率
0.0800

波束功率
10
10
10
10

Calling SDPT3 4.0: 6199 variables, 754 equality constraints

num. of constraints = 754
dim. of sdp var = 1560, num. of sdp blk = 390
dim. of socp var = 450, num. of socp blk = 150
dim. of linear var = 949
dim. of free var = 900 *** convert ublk to lblk

SDPT3: Infeasible path-following algorithms

version predcorr gam expon scale_data
HKM 1 0.000 1 0
it pstep dstep pinfeas dinfeas gap prim-obj dual-obj cputime

0|0.000|0.000|1.1e+02|3.2e+02|2.7e+08| 7.851976e+03 0.000000e+00| 0:0:00| spchol 1 1
1|0.234|0.853|8.3e+01|4.8e+01|9.0e+07| 1.512301e+04 4.229251e+05| 0:0:00| spchol 1 1
2|0.602|0.960|3.3e+01|2.1e+00|3.6e+07| 6.940372e+03 4.700398e+05| 0:0:00| spchol 1 1
3|0.942|1.000|1.9e+00|1.3e-01|1.7e+06| 5.010671e+02 5.336377e+05| 0:0:00| spchol 1 1
4|0.460|0.724|1.0e+00|8.0e-02|8.6e+05| 3.266040e+02 1.821062e+06| 0:0:00| spchol 1 1
5|0.071|0.280|9.6e-01|6.6e-02|2.8e+06| 3.120497e+02 2.037033e+07| 0:0:00| spchol 1 1
6|0.051|0.150|9.1e-01|6.6e-02|1.6e+07| 2.954795e+02 4.092222e+08| 0:0:00| spchol 1 1
7|0.006|0.360|9.1e-01|4.5e-02|4.2e+09| 2.956842e+02 3.253824e+11| 0:0:00| spchol 2 2
8|0.001|0.020|9.0e-01|5.2e-02|7.8e+11| 3.368949e+02 2.571487e+14| 0:0:00| spchol 2 2
9|0.000|0.261|9.0e-01|5.9e-02|3.5e+16| 3.736175e+02 2.157497e+19| 0:0:00| spchol
linsysolve: Schur complement matrix not positive definite
switch to LU factor. splu 2 1
stop: Z not positive definite
10|0.000|0.000|9.0e-01|5.9e-02|3.5e+16| 3.736175e+02 2.157497e+19| 0:0:00|
prim_inf,dual_inf,relgap = 9.05e-01, 5.85e-02, 1.61e-03
sqlp stop: primal problem is suspected of being infeasible

number of iterations = 10
residual of primal infeasibility
certificate (y,Z) = 2.55e-19
reldist to infeas. <= 2.18e-19
Total CPU time (secs) = 0.37
CPU time per iteration = 0.04
termination code = 1
DIMACS: 1.1e+01 0.0e+00 2.2e-01 0.0e+00 -1.0e+00 1.6e-03

Status: Infeasible
Optimal value (cvx_optval): -Inf

P
NaN NaN NaN NaN
NaN NaN NaN NaN
NaN NaN NaN NaN
NaN NaN NaN NaN

错误使用 * (第 55 行)
Disciplined convex programming error:
Invalid numeric values (NaNs) may not be used in CVX expressions.

出错 ljTest (第 365 行)
f = f + trace(Usc(:, :, s, t)) - v_max_Usc(:, s, t)’ * Usc(:, :, s, t) * v_max_Usc(:, s, t);

My questions are 1) how to select suitable input date and how to scale 2) why after adding a second-order cone constraint, the original problem becomes unfeasible

Looking forward to everyone’s suggestions, thank you very much!

Mark_L_Stone · November 21, 2024, 12:38pm

This is your problem. So you should know what sensible input data is. you can’;t expect CVX forum readers to know that.

At some point, when constraints are added to a problem, it can become infeasible. If I have a constraint x >= 5, and add a second order cone constraint norm(x) <= 4, the problem becomes infeasible.

All but section 1 of Debugging infeasible models - YALMIP also applies to CVX.

FastGraduate · November 21, 2024, 1:03pm

Thank you very much for your suggestions. And I will try as you advise.

Help! After adding a second-order cone constraint, the original problem becomes unfeasible

Calling SDPT3 4.0: 6199 variables, 754 equality constraints

version predcorr gam expon scale_data HKM 1 0.000 1 0 it pstep dstep pinfeas dinfeas gap prim-obj dual-obj cputime

number of iterations = 10 residual of primal infeasibility certificate (y,Z) = 2.55e-19 reldist to infeas. <= 2.18e-19 Total CPU time (secs) = 0.37 CPU time per iteration = 0.04 termination code = 1 DIMACS: 1.1e+01 0.0e+00 2.2e-01 0.0e+00 -1.0e+00 1.6e-03

version predcorr gam expon scale_data
HKM 1 0.000 1 0
it pstep dstep pinfeas dinfeas gap prim-obj dual-obj cputime

number of iterations = 10
residual of primal infeasibility
certificate (y,Z) = 2.55e-19
reldist to infeas. <= 2.18e-19
Total CPU time (secs) = 0.37
CPU time per iteration = 0.04
termination code = 1
DIMACS: 1.1e+01 0.0e+00 2.2e-01 0.0e+00 -1.0e+00 1.6e-03