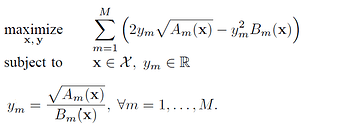Hi everyone! I am currently working on an optimization problem in which my objective function is a sum of ratios, and the optimization variable is a vector. Note that the objective function is quadratically transformed to satisfy convexity. Check the optimization problem below.
The variable vector x has values between 0 and 1, and the auxiliary variable y is a ratio of a function of x.
The problem lies in the denominator of the auxiliary variable. When I convert the problem into CVX form, the following error arises:
Error using .* (line 173)
Disciplined convex programming error:
Cannot perform the operation: {concave} ./ {real affine}
Error in ./ (line 19)
z = times( x, y, './' );
Error in * (line 36)
z = feval( oper, x, y );
Error in / (line 15)
z = mtimes( x, y, 'rdivide' );
It seems that I am not allowed to divide by the sum of the vector x due to its CVX nature. I even tried initializing a variable outside of CVX and trying to relate it, but the function became independent of x. Below you can find a snippet of the code.
So, if you have any suggestions on how to go around this problem, please advise, and thanks in advance. 
cvx_begin
variable b_op(k)
num=sqrt(b_op(1));
denom=sum(b_op);
y=num/denom;
maximize (sum(2.*y.*num - y.^2.*denom))
subject to
b_op >= 0;
b_op <= 1;
cvx_end
I don’t understand the notation. For example, what are A_m(X), B_m(x) ? Doesn’t each term in the objective simplify to \frac{A_m(x)}{B_m(x)}?
Anyhow, the first thing is, how did you prove convexity, i.e., that the objective function is concave? What do you know about the sign of B_m(x)? (I guess you are trying to constrain it to be >= 0 and <= 1)?
Perhaps I did not give a full problem definition. I am solving the fractional optimization problem iteratively. Here are the steps.
Step 1: Initialize x to a feasible value (e.g a vector of ones)
Step 2: Reformulate the objective function using the quadratic transform, i.e. replacing each A_m/B_m with 2y_m\sqrt{A_m}-y_m^2B_m.
Repeat
Step 3: Update y using y_{m}=\frac{\sqrt{A_{m}(\mathrm{x})}}{B_{m}(\mathrm{x})}, \forall m=1, \ldots, M
Step 4: Update x by solving the reformualted convex problem over x for fixed y
until Convergence
It is conditioned that each A_m(x) is concave and each B_m(x) is convex, hereby making it a concave-convex multiple ratio problem. Using this and the non-decreasing nature of the square root function, the quadratic transform is concave in x.
Anyway, I will read the attached FAQ as well.
For each CVX optimization problem, you need to make clear to yourself, and then to us,
What is the input data?
What are the CVX optimization variables?
How the optimal CVX optimization variable values from the just completed optimization are used as input data for the next CVX optimization problem.
I don’t find the mapping between your steps 1-4 and my questions to be clear. You need to make it so.
For this approach, you initialize y (which is the auxiliary variable) and then solve for x. The problem should be convex in terms of the variable x. Then, you use the x to update the auxiliary variable y and solve for a new x. So you iterate between solving for x and updating y until convergence. Hope this helps.
This is exactly what I did. I went back to the literature and tried to solve it this way. It worked out. Thanks for your input.