I have this problem to solve in CVX, I would appreciate somebody to correct my error.
1.The life time of a node under flow r is defined as:
$$T_i®=\frac{B_i}{\sum_{j\in N_i}E_{ij}r_{ij}}$$
- Now the network lifetime as :
$$T_{net}®=min_{i\in N}T_i®$$
3.The following problem wants to find a flow in network that maximize lifetime(which is max(min_{i\in N}T_i(r)))
$$Maximize \ \ T_{net}® \ subject \ to \ \ \sum_{j\in N_i}(r_{ij}-r_{ji}) =S_i, \ \ \forall i \in V \ 0\le r_{ij} \le R_{ij}, \ \ \forall i \in V , \forall j \in N_i $$
-
another form of above problem with additional constraint
$$Maximize \ \ T \ subject \ to \ \ \sum_{j\in N_i}(r_{ij}-r_{ji}) =S_i, \ \ \forall i \in V \ 0\le r_{ij} \le R_{ij}, \ \ \forall i \in V , \forall j \in N_i \ T\sum_{j\in N_i}E_{ij}r_{ij}\le B_i, \ \forall i \in V $$
$$q=\frac1T$$
The author says the following problem is a linear programming that he want to solve in a distributed manner, but I want solve it as is, to test and learn:
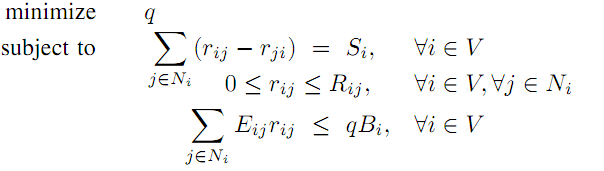
my basic implementation to test for two node is:
(this is a network so B_i is a vector and r_ij is a matrice, the same is true for other variables)
B_i=[5];%initial battery energy of node i
r_ij=[10]; %flow rate from i to j
r_ji=[15]; %flow rate from j to i
S_i=[0.5]; %the rate at which information is generated at node i
E_ij=[0.005]; %The energy consumption for sending a packet from node i to node j
R_ij=[10]; %the maximum flow that a link from node i to node j can support
m=1;n=1;
cvx_begin
variables S_i(1) E_ij(m,n) r_ij(m,n) r_ji(m,n) R_ij(m,n) q;
minimize q
subject to
sum(r_ij-r_ji)==S_i(1);
sum(0.005 * r_ij)<=q*B_i;
-r_ij<=0;
r_ij<= R_ij;
cvx_end
By the way, at the end I want to implement section 4 of this article page 3 and 4,
I’m a beginner both in CVX and optimization so I really appreciate any suggestion that is helpful to implement this subgradeint algorithm(a pseudo code will be fine).
Thanks.
update: I changed some variables, now it works but is my formulation correct in CVX?