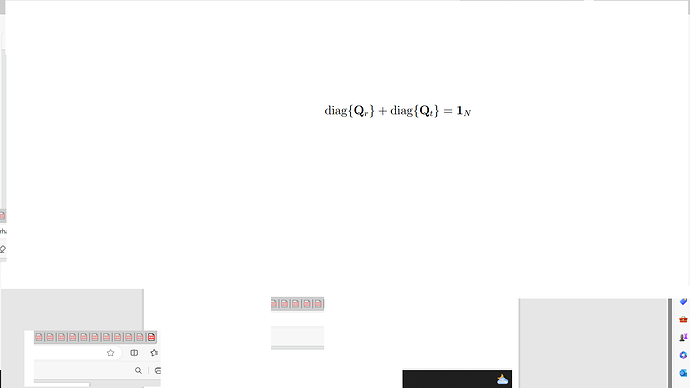
When I run my code, cvx showed the status is failed (other cvx is solved),but i can got the result when the whole code ended
my code is as following :
clc
clear all
M = 4 ; %number of element RIS
K = 1:M;
theta_r_0 = diag(K); %constant first phase
theta_t_0 = diag(K);
NR = 4; % recive antenna
NT = 4; % transmit antenna
ro1 = 2;
ro2 = 2;
N = 4;
w = 10 ;
Pe_vdb = 0:2:8; %dB
Pe_v = 10.^(Pe_vdb./10); %watt
Ne = 1;
Nd = 1;
Ps = 10.^(20./10);
itration = 6;
theta_r_h_0 = diag(theta_r_0)‘;
theta_t_h_0 = diag(theta_t_0)’;
%
theta_r_bar_0 = [theta_r_h_0 1];
theta_t_bar_0 = [theta_t_h_0 1];
Qr_0= (theta_r_bar_0)'(theta_r_bar_0)
Qt_0 = (theta_t_bar_0)'(theta_t_bar_0)
norm_2_Qt_0 = norm(Qt_0);
norm_2_Qr_0 = norm(Qr_0);
normnuc_Qt = norm_nuc(Qt_0);
normnuc_Qr = norm_nuc(Qr_0);
Ex = zeros(1,length(Pe_vdb));
maxro_t = 1.0000e-06;
maxro_r = 1.0000e-06;
for ii = 1:length(Pe_vdb)
ii
Q_E = Pe_v(ii);
c = 0;
j = 0;
for i = 1:itration;
a = theta_r_0;
b = theta_t_0;
h_RD=(1/sqrt(2))*(randn(1,M)+sqrt(-1)*randn(1,M));
h_SR=(1/sqrt(2))*(randn(M,1)+sqrt(-1)*randn(M,1));
h_SD=(1/sqrt(2))*(randn(1,1)+sqrt(-1)*randn(1,1));
H_ER=(1/sqrt(2))*(randn(M,NT)+sqrt(-1)*randn(M,NT));
H_RE=(sqrt(.1)/sqrt(2))*(randn(NR,M)+sqrt(-1)*randn(NR,M));
H_EE=(1/sqrt(2))*(randn(NR,NT)+sqrt(-1)*randn(NR,NT));
while maxro_t> 1.0000e-07 && maxro_r> 1.0000e-07;
for n = 1:N ;
u = H_EE + H_RE*a*H_ER ;
y_max = 1 + (Q_E/Nd)( ( norm( h_RDb*H_ER) ).^2 );
for z = 1:5;
y = 1 + (y_max./5).*(z-1);
%............. Optimization Problem ..............
cvx_begin sdp quiet
variable Z(NT,NT) hermitian;
variable s;
variable f_y;
dual variables p1 p2 p3 p4 p5
minimize f_y;
subject to
p1: s == hermitian_semidefinite(1);
p2: trace(Z) == s;
p3: s + (Q_E/Ne)*trace(Z*( u' )*( u ) ) == 1
p4: (Q_E/Ne)*trace(Z*H_ER'*b'*h_RD'*h_RD*b*H_ER) == s .* (y-1)
p5: Z == hermitian_semidefinite(NT)
f_y - (Q_E/Ne)*trace(Z*(u'*H_RE*b*h_SR*h_SR'*b'*H_RE'*u))== hermitian_semidefinite(1)
cvx_end
if( strcmp( cvx_status, 'Infeasible' ) == 1 );
Exy(z) = 0;
else
Exy(z) = f_y + ( ((Ne/Nd).*(abs(h_SD + h_RD*a*h_SR)^2))./y) ;
end
end
E_xy = nonzeros(Exy);
[l,e] = min(E_xy) ;
if mean(Exy) ~= 0
j = find(Exy==l);
end
y = 1 + (y_max-1)/5*(j-1);
cvx_begin sdp quiet
variable Z(NT,NT) hermitian;
variable s;
variable v;
dual variables p1 p2 p3 p4 p5
minimize v ;
subject to
p1: s == hermitian_semidefinite(1);
p2: trace(Z) == s;
p3: s + (Q_E/Ne)*trace(Z*( u' )*( u ) ) == 1
p4: (Q_E/Ne)*trace(Z*H_ER'*b'*h_RD'*h_RD*b*H_ER) == s .* (y-1)
p5: Z == hermitian_semidefinite(NT)
v - (Q_E/Ne)*trace(Z*(u'*H_RE*b*h_SR*h_SR'*b'*H_RE'*u))== hermitian_semidefinite(1)
cvx_end
%% .......................... W and w_t .............................
if length(cvx_status)==6 && sum(cvx_status == 'Solved')==6;
W = Z/s ;
h_t = real(cvx_optval);
[V D] = eigs(W);
d = real(diag(D));
[d I] = sort(d,'descend');
w_opt = V(:,I(1));
W_opt = W;
else
w_opt = zeros(NT,1);
W_opt = zeros(NT);
h_t = 0;
end
A = Q_E*( H_EE*w_opt + H_RE*a*H_ER*w_opt )*( (H_EE*w_opt + H_RE*a*H_ER*w_opt)')+Ne;
Wr = inv(A)*H_RE*b*h_SR/norm(inv(A)*H_RE*b*h_SR);
ak1 = ( diag(h_RD) )*h_SR;
ak1_bar = [ak1',h_SD']' ;
Ak1 = ak1_bar*(ak1_bar');
ak2 = ( diag(h_RD) )*H_ER*w_opt ;
ak2_bar = [ak2',0]';
Ak2 = ak2_bar*(ak2_bar') ;
ak3 = ( diag(Wr'*H_RE) )*h_SR;
ak3_bar = [ak3',0]';
Ak3 = ak3_bar*(ak3_bar');
ak4 = ( diag(Wr'*H_RE) )*H_ER*w_opt;
g = Wr'*H_EE*w_opt;
ak4_bar = [ak4',g]';
Ak4 = ak4_bar*(ak4_bar');
%............. Optimization Problem ..............
cvx_begin sdp;
variables x y T ;
variable Qt(M+1,M+1) ;
variable Qr(M+1,M+1) ;
expression Qt_bar_n;
expression Qr_bar_n;
expression t2;
expression t6;
[Utt Rtt] = eigs(Qt_0,1,'LM');
Ut = abs(Utt)
[Urr Rrr] = eigs(Qr_0,1,'LM');
Ur = abs(Urr)
Qt_bar_n = norm_2_Qt_0+trace(Utt*Utt'*(Qt-Qt_0));
Qr_bar_n = norm_2_Qr_0+trace( Urr*Urr'*(Qr-Qr_0));
% t1= square( trace(Ak3Qt)-trace(Ak2Qt) );
t2 = real( (-2).*( trace(Ak3.*Qt_0)+trace(Ak2.Qt_0) )( trace(Ak3.*Qt)+trace(Ak2.*Qt) ) ) ;
t3 = real((trace(Ak3.*Qt_0)+trace(Ak2.*Qt_0)).^2) ;
t6 = real((-2).*( trace(Ak4.*Qr_0)-trace(Ak1.*Qr_0) )*( trace(Ak4.*Qr)-trace(Ak1.*Qr) ));
t7 = real(( trace(Ak4*Qr_0)-trace(Ak1*Qr_0) ).^2);
T == [x y];
minimize ( prod_inv(T)+ro1*( norm_nuc(Qt)- Qt_bar_n )+ro2*( norm_nuc(Qr)-Qr_bar_n) );
subject to ;
4*inv_pos(x)+square( trace(Ak3*Qt)-trace(Ak2*Qt) )+t2+t3 < 0;
square( trace(Ak4*Qr)+trace(Ak1*Qr) )+t6+t7-4*y < 0;
%
Qt>0;
Qr>0;
cvx_end;
Qt_n = Qt;
Qr_n = Qr;
th_bar_r = sqrt(diag(Qr_n))';
th_tilr = th_bar_r(:,1:end-1);
theta_r = diag(th_tilr');
th_bar_t = sqrt(diag(Qt_n))';
th_tilt = th_bar_t(:,1:end-1);
theta_t = diag(th_tilt');
a = theta_r;
b = theta_t;
theta_r_hn_0 = diag(theta_r)‘;
theta_t_hn_0 = diag(theta_t)’;
%
theta_r_barn_0 = [theta_r_hn_0 1];
theta_t_barn_0 = [theta_t_hn_0 1];
Qr_0= (theta_r_barn_0)'(theta_r_barn_0);
Qt_0 = (theta_t_barn_0)'(theta_t_barn_0);
norm_2_Qt_0 = norm(Qt_0);
norm_2_Qr_0 = norm(Qr_0);
normnuc_Qt = norm_nuc(Qt_0);
normnuc_Qr = norm_nuc(Qr_0);
end
ro1 = w*ro1;
ro2 = w*ro2;
Qt_n = Qt;
Qr_n = Qr;
maxro_t = max( norm_nuc(Qt_n) - norm(Qt_n) );
maxro_r = max( norm_nuc(Qr_n) - norm(Qr_n) );
end
SINR_d = Ps*(abs(h_SD + h_RD*a*h_SR)^2)/(Q_E*(abs( h_RD*b*H_ER*w_opt)^2) + Nd);
SINR_e = Ps*(abs(Wr'*H_RE*b*h_SR)^2)/(Q_E*(abs(Wr'*H_EE*w_opt + Wr'*H_RE*a*H_ER*w_opt )^2) + Ne);
if SINR_e >= SINR_d;
c = c + 1;
end
end
Ex(ii) = c./itration;
end
figure(1)
plot(Pe_vdb,Ex)
hold on
grid on
box on