expression abs function returns incorrect value

Tai_Le · July 14, 2025, 12:00pm

for m = 1:para.D2D
if m ~= i
g_3(i,m) = h_D2DT_D2DR(m,i) + Q.‘*diag(h_s_D2DR(:,i)’)*h_D2DT_s(m,:).';
h = g_3(i,m);
k = abs(h);
sr2(i) = sr2(i) + p(m)*square_abs(g_3(i,m));
end
end
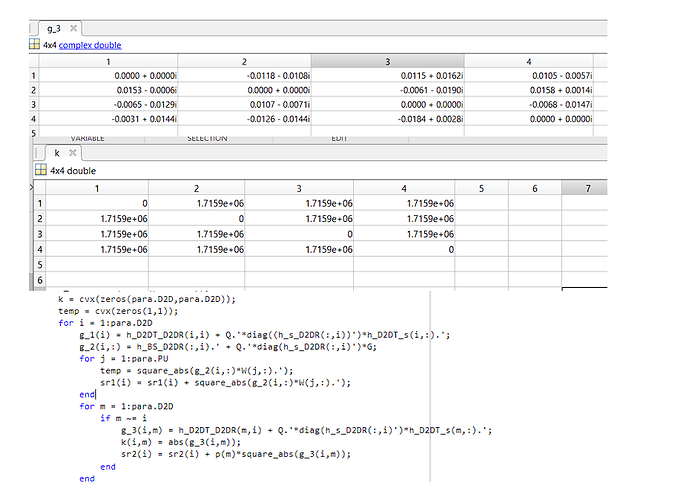
I have a problem that when using the above loop in cvx with (expression g_3 and variable Q(para.N) complex) then when h = 1.05e-04 + 3.4e-06i then k = abs(h) = 2.23e+11. why is there such a big deviation in the result in cvx.
Does calculating the abs of an expression directly in cvx cause that phenomenon?

Mark_L_Stone · July 14, 2025, 12:04pm

I have no idea what you’ve done. It’s not clear what of this even pertains to CVX.

If you show a complete reproducible CVX problem, with all input data and CVX and solver output, perhaps someone can say something.

Tai_Le · July 14, 2025, 1:08pm

clearvars
clc
location_BS=[-50;0;0];
location_STAR=[0;0;0];
%The users are uniformly distributed in a circle centered at the STAR with the radius of 3 m
radius(1)=3;
radius(2)=3;
R_D2D_min = 0.005;
R_PU_min = 0.1;
P_BS_max = 0.26;
P_D2D_max = 0.264;
c=10;
para = para_init();
para.N = para.STAR_size(1)*para.STAR_size(2);
%Generate channels
[BS_array, STAR_array] = generate_arrays(para);
%[G,h_s_PU,h_D2DT_s,h_BS_PU,h_s_D2DR,h_D2DT_PU,h_D2DT_D2DR,h_PU_D2DT,h_PU_s] = fake_channel(para);
[G,h_s_PU,h_D2DT_s,h_BS_PU,h_s_D2DR,h_D2DT_PU,h_D2DT_D2DR,h_PU_D2DT,h_PU_s,h_BS_D2DR] = generate_channel(para, BS_array, STAR_array);

G = 10^2G;
h_s_PU = 10^2h_s_PU;
h_D2DT_s = 10^2h_D2DT_s;
h_BS_PU = 10^4h_BS_PU;
h_s_D2DR = 10^2h_s_D2DR;
h_D2DT_PU = 10^4h_D2DT_PU;
h_D2DT_D2DR = 10^2h_D2DT_D2DR;
h_PU_D2DT = 10^4h_PU_D2DT;
h_PU_s = 10^2h_PU_s;
h_BS_D2DR = 10^4h_BS_D2DR;

B = 1;
Wband = 10; %MHz
Noise_var = 1; % noise variance N0/2=-174dBm/Hz
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% %%%%%%%%% CVX OPT - All BSs active %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% %%%%%%%% Iterative Algorithm for EEmax %%%%%%%%%%%%%%%%%%
err_tol = 1;
maxOut = 100;
Q_history = cell(1, maxOut);
sum_rate_history = zeros(1, maxOut +1);
sum_rate_history(1) = 0;
sum_rate_prev = -inf;
iter = 0;
[W,p]= Beam_Power(para,P_BS_max,P_D2D_max,h_BS_PU);
while (err_tol > 1e-4 && iter < maxOut)
iter = iter + 1;
if (iter == 1)
Q_prev = phase_shift_matrix_2(para.N);
else
Q_prev = Q;
end
s = zeros(para.PU);
s2_v = zeros(para.PU);
s1_v = zeros(para.PU);
g_BS_PU_v = zeros(para.M,para.PU);
g_D2DT_PU_v = zeros(para.D2D);
a = zeros(para.PU);
b = zeros(para.D2D);
ar = zeros(para.D2D);
br = zeros(para.D2D);
for i = 1:para.PU
for j = 1:para.PU
g_BS_PU_v(:,i) = h_BS_PU(:,i).’ + Q_prev.‘*diag(h_s_PU(:,i)’)*G;
if j ~= i
s1_v(i) = s1_v(i) + abs(g_BS_PU_v(:,i).‘*W(j,:).’)^2;
end
end
for d= 1:para.D2D
g_D2DT_PU_v(i) = h_D2DT_PU(d,i).’ + Q_prev.‘*diag(h_s_PU(:,i)’)*h_D2DT_s(d,:).‘;
s2_v(i) = s2_v(i) + p(d)*abs(g_D2DT_PU_v(i))^2;
end
s(i) = abs(g_BS_PU_v(:,i).’*W(i,:).‘)^2/(s1_v(i)+s2_v(i)+ Noise_var);
a(i) = log(1 + s(i));
b(i) = s(i)/(1 + s(i));
end
g_v_1 = zeros(para.D2D);
g_v_2 = zeros(para.D2D,para.M);
g_v_3 = zeros(para.D2D,para.D2D);
sr2_v = zeros(para.D2D);
sr1_v = zeros(para.D2D);
for i = 1:para.D2D
g_v_1(i) = h_D2DT_D2DR(i,i) + Q_prev.’*diag((h_s_D2DR(:,i))‘)*h_D2DT_s(i,:).’;
for j = 1:para.PU
g_v_2(i, = h_BS_D2DR(:,i).’ + Q_prev.‘*diag(h_s_D2DR(:,i)’)*G;
sr1_v(i) = sr1_v(i) + abs(g_v_2(i,:)*W(j,:).‘)^2;
end
for m = 1:para.D2D
if m ~= i
g_v_3(i,m) = h_D2DT_D2DR(m,i).’ + Q_prev.‘*diag((h_s_D2DR(:,i))’)*h_D2DT_s(m,:).';
sr2_v(i) = sr2_v(i) + p(m)*abs(g_v_3(i,m))^2;
end
end
ar(i) = log(1 + (p(i)*abs(g_v_1(i))^2)/(sr1_v(i)+sr2_v(i)+ Noise_var));
br(i) = ((p(i)*abs(g_v_1(i))^2)/(sr1_v(i)+ sr2_v(i) + Noise_var))/(1+((p(i)*abs(g_v_1(i))^2)/(sr1_v(i)+ sr2_v(i)+ Noise_var)));
end

cvx_begin
variable Q(para.N) complex
expression R_PU(para.PU)
expression sum_PU
expression s1(para.PU)
expression s2(para.PU)
expression sr1(para.D2D)
expression sr2(para.D2D)
expression R_D2D(para.D2D)
expression temp
expression g_BS_PU(para.M,para.PU)
expression g_D2DT_PU(para.D2D)
expression g_1(para.D2D)
expression g_2(para.D2D,para.M)
expression g_3(para.D2D,para.D2D)
expression k(para.D2D,para.D2D)
s1 = cvx(zeros(para.PU));
s2 = cvx(zeros(para.PU));
sr1 = cvx(zeros(para.D2D));
sr2 = cvx(zeros(para.D2D));
g_1 = cvx(zeros(para.D2D));
g_2 = cvx(zeros(para.D2D,para.M));
g_3 = cvx(zeros(para.D2D,para.D2D));
g_BS_PU = cvx(zeros(para.M,para.PU));
g_D2DT_PU = cvx(zeros(para.D2D));
R_D2D = cvx(zeros(para.D2D));
k = cvx(zeros(para.D2D,para.D2D));
temp = cvx(zeros(1,1));
for i = 1:para.D2D
g_1(i) = h_D2DT_D2DR(i,i) + Q.‘*diag((h_s_D2DR(:,i))’)*h_D2DT_s(i,:).‘;
g_2(i, = h_BS_D2DR(:,i).’ + Q.‘*diag(h_s_D2DR(:,i)’)*G;
for j = 1:para.PU
temp = square_abs(g_2(i,:)*W(j,:).‘);
sr1(i) = sr1(i) + square_abs(g_2(i,:)*W(j,:).’);
end
for m = 1:para.D2D
if m ~= i
g_3(i,m) = h_D2DT_D2DR(m,i) + Q.‘*diag(h_s_D2DR(:,i)’)h_D2DT_s(m,:).';
k(i,m) = abs(g_3(i,m));
sr2(i) = sr2(i) + p(m)square_abs(g_3(i,m));
end
end
R_D2D(i) = B * (ar(i) + br(i) * (2 - abs(g_v_1(i))^2inv_pos(2real((g_1(i))*conj(g_v_1(i)) - abs(g_v_1(i))^2)) - (sr1(i) + sr2(i) + Noise_var)/(sr1_v(i) + sr2_v(i) + Noise_var)));
end
for i = 1:para.PU
for j = 1:para.PU
g_BS_PU(:,i) = h_BS_PU(:,i).’ + Q.‘*diag(h_s_PU(:,i)’)*G;
if j ~= i
s1(i) = s1(i) + square_abs(g_BS_PU(:,i).‘*W(j,:).’);
end
end
for d = 1:para.D2D
g_D2DT_PU(i) = h_D2DT_PU(d,i).’ + Q.‘*diag(h_s_PU(:,i)’)h_D2DT_s(d,:).';
s2(i) = s2(i) + p(d)square_abs(g_D2DT_PU(i));
end
R_PU(i) = B * (a(i) + 2b(i) - b(i)(abs(g_BS_PU_v(:,i).‘*W(i,:).’)^2)inv_pos(2real((g_BS_PU(:,i).‘*W(i,:).’)*conj((g_BS_PU_v(:,i).‘W(i,:).'))) - abs(g_BS_PU_v(:,i).'W(i,:).')^2) - b(i)(s1(i) + s2(i) + Noise_var)/(s1_v(i) + s2_v(i) + Noise_var));
end
sum_PU = sum(R_PU);
maximize(sum_PU)
subject to
for i =1:para.N
square_abs(Q(i)) <=1;
end
for i = 1:para.PU
%R_PU(i) >= R_PU_min;
end
for i = 1:para.D2D
%R_D2D(i) >= R_D2D_min;
end
cvx_end
% Kiểm tra trạng thái CVX
if strcmp(cvx_status, ‘Infeasible’)
error(‘Bài toán không khả thi. Kiểm tra lại ràng buộc hoặc khởi tạo.’);
end
% Cập nhật Q
Q = double(Q);
s1 = double(s1);
s2 = double(s2);
%Tính sum rate của PU
for i= 1:para.PU
SINR(i) = Blog(1 + abs(g_BS_PU(:,i).’*W(i,:).')^2/(s1(i)+s2(i)+ Noise_var));
end
sum_rate_history(iter + 1) = sum(SINR);
Q_history{iter} = Q;
err_tol = sum_rate_history(iter + 1) - sum_rate_prev;
sum_rate_prev = sum_rate_history(iter + 1);
end
limit = iter + 1;
limited_iterations = 1:min(limit, length(sum_rate_history));
limited_sum_rate = sum_rate_history(limited_iterations);
% Vẽ đồ thị
figure;
plot(limited_iterations, limited_sum_rate, ‘-o’, ‘LineWidth’, 2);
grid on;
xlabel(‘Số vòng lặp’);
ylabel(‘Tổng tốc độ dữ liệu (Sum Rate) [bps]’);
title(‘Biến thiên của tổng tốc độ dữ liệu theo số vòng lặp’);
legend(‘Sum Rate History’, ‘Location’, ‘best’);
toc;

Here is my entire code. I checked the values in the workspace and found that with the values of the g_3 matrix generating the k matrix gives an unreasonable result.

Tai_Le · July 14, 2025, 1:11pm

Mark_L_Stone · July 14, 2025, 3:01pm

The apparent inconsistency is a feature of CVX (even if undesirable), not a bug… g_3 is an expression, not a CVX variable, and therefore the value populated for it after cvx_end may not reflect its true value used in the optimization.

CVX variables are populated with their optimal values after cvx_end, but CVX expressions (whether declared as such or not) are not necessarily populated with their optimal values after cvx_end. So to get the optimal values of CVX expressions, you need to compute them after cvx_end, starting with the CVX optimal variable values.

The optimization is performed correctly even though the populated values for the expressions might not be correct. That reflects a CVX design decision. At the expense of some additional computation, CVX could have been written to automatically populate CVX expressions with their final optimal value, but was not designed that way. At minimum, the CVX Users’ Guide should have been clear and explicit about this (design decision), but is not.