Error using sqrtm Input must be a single or double matrix

1

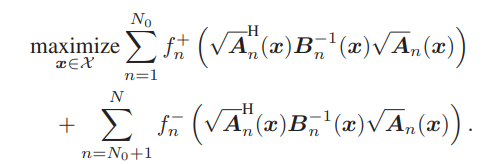
image
I have reformulated an optimization problem using fractional programming as above where fn+(.) is a concave increasing function, and fn-(.) is a concave decreasing function , but as the optimization variable x is inside the square root of the matrix, im getting the following error,
Error using sqrtm
Input must be a single or double matrix.
kindly help me resolve this. Below is the cvx snippet
cvx_begin
variable alpha1_MAT(size(M1M1’)) hermitian semidefinite
expression C_MAT
expression D_MAT
expression R
expression P
expression Gamma_L
expression Y_MAT_tilde
expression Qn_eav
C_MAT=alpha1_MATPt*(M1M1’);
D_MAT=np_eaves(G2G2’)+ Pt(M2M2’)-Ptalpha1_MAT*(M2M2’);
R=sqrtm(C_MAT);
P=sqrtm(D_MAT);
Gamma_L=alpha1_MATlambda;
Y_MAT_tilde=inv(C_MAT)P’;
Qn_eav=(P’Y_MAT_tilde)+(Y_MAT_tilde’P)-(Y_MAT_tilde’C_MATY_MAT_tilde);
maximize (1/(MN)(sum(log2(1 + Gamma_L)))+ log2(1/(det(eye(MN)+inv(Qn_eav)))));
subject to
0 <= diag(alpha1_MAT) <= 1;
cvx_end;

2

sqrtm can’t be applied to CVX expressions or variables. Accordingly,you will not find it it listed in Reference guide — CVX Users' Guide .

i will assume your problem is not a convex optimization problem, unless you show a rigorous (not hand-waving) convexity proof.

Please carefully read

3

image
image474×715 83.9 KB

image
Instead of sqrtm, I have also tried using cholskey decomposition , which also gives the same error, forget the cvx code given by me for the time being, I have attached snap shots of the formulation proving to be convex, where the optimization variable is with in the square root of a matrix. Kindly help me to formulate the same in the cvx.

4

Apparently, the original problem is not convex. The authors propose an alternating optimization, which you did not implement. I don’t understand the notation and conventions, so i can’t verify that the subproblems in the alternating optimization are convex and enterable in CVX. I leave that to you.

1 Like