Hi
I am trying to solve the following optimization problem with the help of CVX, but I encounter the following error?
I would appreciate it if anyone can help me.
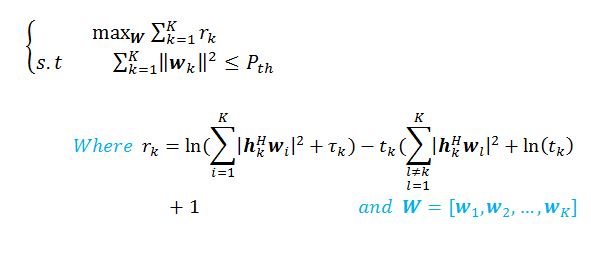
this is my code in following:
Hi
I am trying to solve the following optimization problem with the help of CVX, but I encounter the following error?
I would appreciate it if anyone can help me.
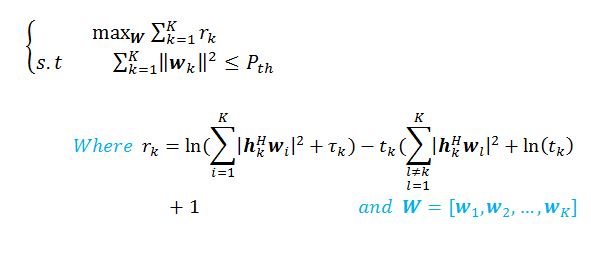
this is my code in following:
Have you proven that the log term in r_k is concave w.r.t the variable W? I will assume it is not until you show otherwise.
Dear Mark, Thanks for your prompt response to the questions.
Given the second-order derivative of a composition function, I think my optimization problem is also concave.
Your h is log which is nondecreasing. So if g is concave (the rule above the highlighted rule), f is concave. That rule is implemented in CVX: log(concave) is concave. Yours is log(convex).
You are right.
I didn’t notice the non-increasing phrase in highlighted part.
I used the presented lemma in the
https://ieeexplore.ieee.org/document/8972400 paper to solve my problem.
In this paper, before Eq. (9)(10), problem P1.3 or P1.5 is convex, and on the other hand, maximized the cost function!! I was confused because of this.
Dear Mark, I found that my problem is neither convex nor concave.
But by converting norm to trace function, which is the same as changing the convex function “g” to affine, the problem becomes concave.
Thanks for spending time to respond.