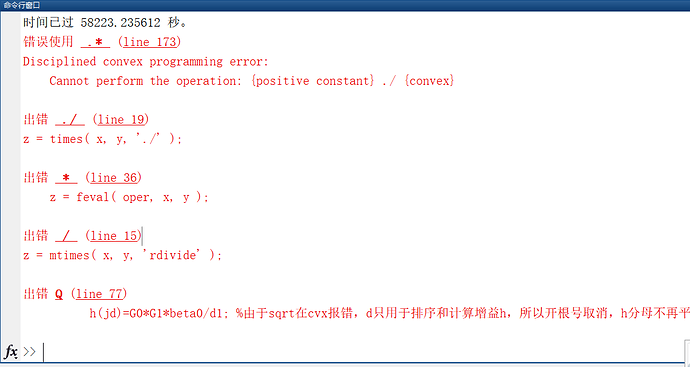
Disciplined convex programming error: Cannot perform the operation: {positive constant} ./ {convex} ,
which in
h(jd)=G0* G1* beta0/d1;
I don’t know how to correct this mistake, please help me.
Code:
while 1
cvx_begin
% variable q1_opt(1,2)
% variable q2_opt(1,2)
variable q1_xopt(1,length(H))
variable q1_yopt(1,length(H))
variable q2_xopt(1,length(H))
variable q2_yopt(1,length(H))
expression tempRate3(2U,Omax)
expression f3(2U,Omax)
expression g3(1,Omax)
expression E3(2,Omax)
expression M3(Omax)
q1_opt=[q1_xopt(1,zz) q1_yopt(1,zz)];
q2_opt=[q2_xopt(1,zz) q2_yopt(1,zz)];
for jre1=1:U
re2(jre1)=sum((q1_opt-W(jre1,:)).^2 ,2);
end
for jre2=U+1:U*2
re2(jre2)=sum((q2_opt-W(jre2,:)).^2 ,2);
end
re=re2';
d(:,zz)=H(zz).^2+re;
%计算信道增益h并排序--------------------------------------------------------
G0=10;
G1=10;
beta0=0.00001; % beta0=-50dB 10log10转换
for jd=1:length(re)
d1=d(jd,zz); h(jd)=G0*G1*beta0/d1; % Disciplined convex programming error: Cannot perform the operation: {positive constant} ./ {convex}
end
sort1=h(1:24); % 1行n列,1*24double
for i=1:24
for j=1:24-i
if sort1(1,j)>sort1(1,j+1)
temp=sort1(1,j);
tempx=W48(j,1);
tempy=W48(j,2);
rechange=re(j,1);
sort1(1,j)=sort1(1,j+1);
W48(j,1)=W48(j+1,1);
W48(j,2)=W48(j+1,2);
re(j,1)=re(j+1,1);
sort1(1,j+1)=temp;
W48(j+1,1)=tempx;
W48(j+1,2)=tempy;
re(j+1,1)=rechange;
end
end
end
for l=1:L
E3(l)=c1*norm(vSolution1(l))^3+c2/norm(vSolution1(l));
end
g3(1,o)=sum(E3(:));
M3(o)=f3(48)-elta3(o)*g3(1,o);
cvx_end
elta3(o+1)=f3(48)/g3(1,o);
if abs(M3(o)-EESolution3)>delta && o<Omax
o=o+1;
else
break;
end
end
end