Error Disciplined convex programming error

Nonconvex
1

I want the Kirsch operator to act on the variable x with cvx.
Kirsch operator at wikipedia

The Kirsch operator or Kirsch compass kernel is a non-linear edge detector that finds the maximum edge strength in a few predetermined directions. It is named after the computer scientist Russell Kirsch.
The reason I want to do this is because I want to solve the following equation using cvx.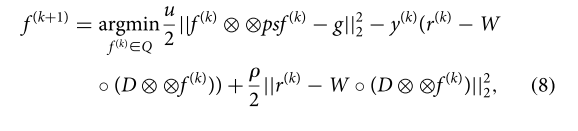タイトルなし

D is the kirsh operator. Equation(8) is part of ADMM.

“”"""""""""""""""""""""""""""""""""""""""""""""""""""""""""
`cvx_begin
variable x(n,n)
x1=kirsh_mat * x
x2=kirsh_mat2 * x

z=max(x1,x2);

minimize( norm(A* x  - b, 2 )+norm(z) )

cvx_end`
“”""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""

I got the following error message:

error: cvx/norm ( 101)
error( ‘Disciplined convex programming error:\n
Cannot perform the operation norm( {%s}, %g )\n
when the first argument is a matrix.’, cvx_class(
xt ), p );

error: cvxtest ( 39)
minimize( norm(PSF_mat * x - b, 2 )+norm(Obje) )

Is it possible to compare the array usage for a cvx variable, return the larger element, and calculate its norm?

2

The argument of norm must be affine. Have you shown that your problem is convex? I will mark it as non-convex until you show it otherwise.

3

Maybe you can handle this by use of the non-convex max formulation approach shown in https://yalmip.github.io/tutorial/logicprogramming . That will then make the argument of norm affine.

4

Thank you for your reply. I think the Kirsch operator is a non-linear process. So maybe I have a non convex formulation .I will check the HP that you introduced.
Thank you !