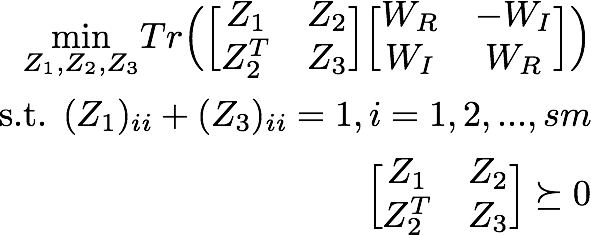Hello CVX Forum Users,
I am trying to solve a magnitude least squares fit using the CVX solver. I have run into an issue with my equality constraints. I limit the sum of two of my variables to have diagonals of 1 in one of my problem constraints. This is outlined in lines 7-9 below. However when the solver completes it always sets all values of the diagonals of Z1 and Z3 to 0.5 which does meet the constraints of the problem but does not fit my actual problem bounds because it is overly constraining. Is there something wrong with how I am stating these equality constraints that is limiting their possible values?
1 cvx_begin sdp
2 cvx_precision best
3 cvx_solver SeDuMi
4 variable Z1(sm, sm)
5 variable Z2(sm, sm)
6 variable Z3(sm, sm)
7 M = [Z1 Z2; Z2’ Z3];
8 M == semidefinite(2*sm);
9 diag(Z1) + diag(Z3) == ones(sm,1);
10 minimize( trace(M * Wreal) )
11 cvx_end
In order to help you, I think we need to know what your “actual problem bounds” are. As you say, your constraints as currently specified are being satisfied.
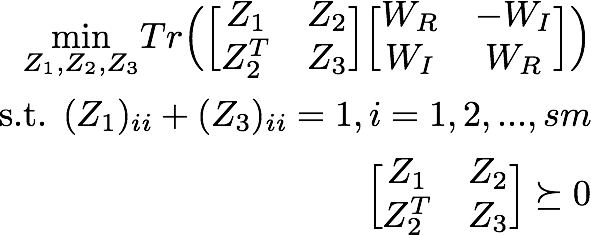
I have attached the mathematical formulation of my problem above. It is a relaxation of magnitude least squares problem aka min(|Ax|-b) for some combination weight x. The issue with the constraint giving 0.5 for all diagonals is that that is where the weights for solution come from so if they are all 0.5 the fit for the problem is just a straight sum of the inputs.
Can you confirm that as I laid out my constraint in code matches my layout of the constraint in formula. If this is this case then I need to further explore what the issue is with my optimization but I wanted to troubleshoot this first.
Thank you for the help,
Olivia
I believe you have correctly implemented in CVX the math formulation you showed. So your issue is with the math formulation. Because the readers/answerers on this forum don’t know what you really want to model and how you want it to behave, it is incumbent on you to figure out that part.
For sure, thank you for confirming that constraint for me.
Cheers,
Olivia
Are you try to implement the convex relaxation of (8), i.e., (10) in https://pdfs.semanticscholar.org/95c8/e14e19ec0984ca12b2ea0aefbf8833bf79d5.pdf ? Note: I found this by searching for magnitude least squares , which I never head of before.
I just made up some random data with data apparently in the form of Wreal (not sure I did it right, however). I ran the problem and constraints were satisfied, but not all diagonal; elements of Z1 and Z3 were 0.5. rank(M) was 2… So I suppose your getting all 0.5 values on the diagonal is due to the particular Wreal you used?
Yes that algorithm is what I am trying to implement, I was using his thesis for my reference. I am attempting to use it to solve a problem in MRI physics.
Glad to hear you got something different, it may be just my form of Wreal. Would you be willing to share your example?
Thank you,
Olivia
I didn’t really know what the requirements are for Wreal, so I made up psd WR and for the heck of it, psd WI to hopefully meet (and go beyond) any requirements. Is this a valid Wreal? I have no idea.
By the way, the original problem I ran had sm = 4, and also produced rank 2 M. I then ran the below with sm = 2 so that Wreal displays better (smaller). That M also had rank 2. As did a problem I ran with sm = 6 and non-symmetric non-psd WR and WI.
sm=2;WR=rand(sm);WR=WR*WR';WI=rand(sm);WI=WI*WI';Wreal=[WR -WI;WI WR]
Wreal =
0.267934013795967 0.309990434085435 -0.648937377442892 -0.045852247130874
0.309990434085435 0.359539643077682 -0.045852247130874 -0.069750748153039
0.648937377442892 0.045852247130874 0.267934013795967 0.309990434085435
0.045852247130874 0.069750748153039 0.309990434085435 0.359539643077682
>> cvx_begin sdp
cvx_precision best
cvx_solver SeDuMi
variable Z1(sm, sm)
variable Z2(sm, sm)
variable Z3(sm, sm)
M = [Z1 Z2; Z2' Z3];
M == semidefinite(2*sm);
diag(Z1) + diag(Z3) == ones(sm,1);
minimize( trace(M * Wreal) )
cvx_end
Calling SeDuMi 1.34: 10 variables, 2 equality constraints
------------------------------------------------------------
SeDuMi 1.34 (beta) by AdvOL, 2005-2008 and Jos F. Sturm, 1998-2003.
Alg = 2: xz-corrector, Adaptive Step-Differentiation, theta = 0.250, beta = 0.500
eqs m = 2, order n = 5, dim = 17, blocks = 2
nnz(A) = 4 + 0, nnz(ADA) = 4, nnz(L) = 3
it : b*y gap delta rate t/tP* t/tD* feas cg cg prec
0 : 6.70E+00 0.000
1 : -6.65E-02 1.63E+00 0.000 0.2427 0.9000 0.9000 1.86 1 1 1.4E+00
2 : 2.02E-02 6.61E-02 0.000 0.0406 0.9900 0.9900 1.30 1 1 2.7E-01
3 : 7.56E-03 3.37E-04 0.000 0.0051 0.9990 0.9990 1.00 1 1 6.0E-03
4 : 7.49E-03 1.04E-08 0.000 0.0000 1.0000 1.0000 1.00 1 1 1.9E-07
5 : 7.49E-03 1.83E-14 0.000 0.0000 1.0000 1.0000 1.00 1 1 3.7E-13
6 : 7.49E-03 4.43E-16 0.004 0.0243 0.9906 0.9900 1.00 5 5 3.1E-16
Run into numerical problems.
iter seconds digits c*x b*y
6 0.1 Inf 7.4927887028e-03 7.4927887028e-03
|Ax-b| = 8.9e-16, [Ay-c]_+ = 1.5E-16, |x|= 1.4e+00, |y|= 6.5e-02
Detailed timing (sec)
Pre IPM Post
7.001E-03 6.400E-02 1.992E-03
Max-norms: ||b||=1, ||c|| = 6.199809e-01,
Cholesky |add|=0, |skip| = 1, ||L.L|| = 1.
------------------------------------------------------------
Status: Solved
Optimal value (cvx_optval): +0.00749279
>> disp(Z1)
0.580637842115486 -0.580637842115486
-0.580637842115486 0.580637842115486
>> disp(Z3)
0.419362157884513 -0.419362157884513
-0.419362157884513 0.419362157884513
>> eig(M)
ans =
-0.000000000000000
0.000000000000000
0.836092672098437
1.163907327901561
Yeah for his implementation W is positive semidefinite. Thank you for this example, it’s helpful to see it working. I think it is my implementation of W so I am going to start with these simpler tests and work up to my problem.
Thanks again,
Olivia