Hi, everyone!
Recently, I’m really comfused about “Elastic net” using CVX package. Here is the details:
I compared the results from lasso.m (MATLAB buld-in function) and glmnet.m (glmnet_matlab tool; https://web.stanford.edu/~hastie/glmnet_matlab/). I found their results great different. Especially, the results from CVX seemd not so sparse (some of Betas should be zero), although there were lots of small number, such as -3.07e-09.
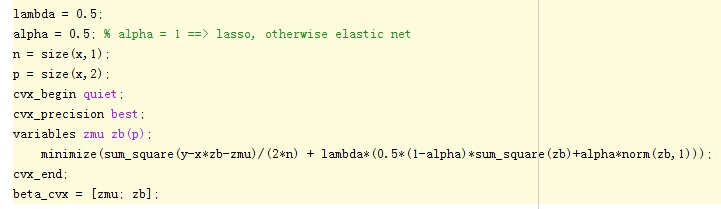
The scripts of “Elastic net” problem in CVX are as follow:
So, I want to know how can I get the “really” sparse results using CVX.
Thanks
The reporting of very small magnitude numbers, such as -3.07e-09, rather than exactly zeros, is an artifact of the solvers called by CVX. It may be reasonable to consider these to be exactly zero. You should be able to post-process the solution reported by CVX to adjust values, whose magnitude is below some threshold, to be exactly equal to zero. A reasonable threshold might perhaps be 1e-6 or thereabouts.
zero_threshold = 1e-6
zb(abs(zb) <= zero_threshold) = 0;
Also, in the future, rather than using images, please copy and paste MATLAB/CVX code and output into your post and use the Prefromatted text option on it
Thanks Mark. It will help a lot. However, I have another confusion. How should I set the reasonable threshold according to my data? What if all of my predictor variables have great magnitudes, such as 4,601,395, while all of my response variable have a pretty small magnitude, such as 0.0077. Under this situation, the actual Beta of predictor variables might be very small even smaller than 1e-6.
Really appreciated it 
Discerning question. In general, you should try to scale your data (choose units) to try to avoid this situation. Scale your response variables to be closer to 1 in magnitude if you can. And try to scale your predictor variables to also be somewhat close in magnitude to 1. That will make the solver the “happiest”.
There is no perfect and clean solution. I did write “perhaps”, and chose not to get into an extended discussion on the subject of choosing the threshold. If your actual exactly optimal solution has argmin values of 1e-8, say, due to magnitude of problem data, then you are likely to be in trouble and not have an effective way of choosing a zero threshold to apply to argmin values obtained from a double precision interior point solver. So see paragraph above.
It may be that you are better off using glmnet, which is more specialized and presumably efficient for ellasticnet problems than is CVX and the solvers it calls. But I’m sure good scaling is also a good thing when using glmnet.
I will try to scale the data first. Thanks a lot.