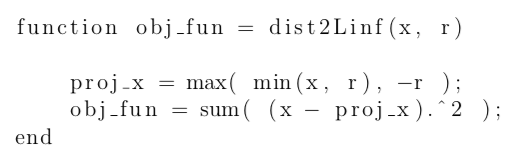Hi,
I need to solve an unconstrained convex minimization problem in which a part of my objective function is the squared Eucledian distance of the choice vector from the ball of the L-infinity norm with radius r>0.
The function reads:
The function is convex.
So far, I have been able to code it without complying to the DCP ruleset and I’ve been using optimization solvers such as fminunc on the objective function or fsolve on the gradient, which is simple to compute. However, as I do not fully trust the solutions provided by these solvers (the whole optimization problem is actually complex, but convex!), I would like to code it, if possible, according to the DCP ruleset. I tried and failed!
My codes to compute this function without complying to the DCP ruleset is:
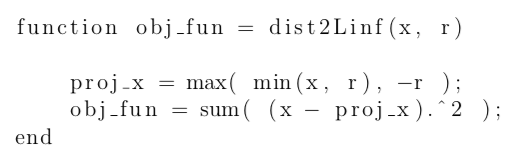
Thank you!
0.5*proj(0) + 0.5*proj(2*r) = 0.5*r < proj(0.5*0 + 0.5*(2*r)) = proj(r) = r
so proj(x) is not convex.
Am I missing something?
Anyhow,read chapter 8 of http://web.stanford.edu/~boyd/cvxbook/
More fun at “Convex Optimization and Euclidean Distance Geometry” by Jon Dattorro https://meboo.convexoptimization.com/access.html
Hi Mark,
thanks for your answer. I will read the chapter you mention.
However my problem is not theoretical: I know that function is convex as it is the convex conjugate of another function I am playing with for a while.
I can prove it, but a simple graph can be more useful.
Here I plot the function (blue line) and its gradient (blue dashed line) vs one component of the choice vector x.
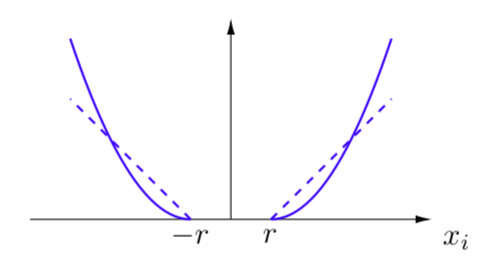
So the fact that proj(x) is not convex does not imply that dist2Linf is not, but now that you point that out it might be the reason why I cannot write it as it is in CVX…