What I want to achieve here is that S must be a positive semidefinite matrix. Just like this:
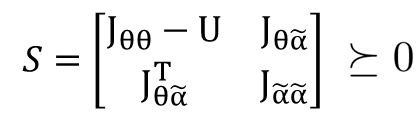
Where U is an optimize variable, and it’s positive semidefinite, as:
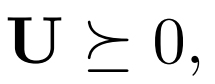
J_θθ, J_(θα ̃),J_(α ̃α ̃) are the expression of another optimize variable T.
The results of some MATLAB code runs are as follows

Here, J_pp∈1×1 means J_θθ, J_pa∈1×2 means J_(θα ̃), and J_aa∈2×2 means J_(α ̃α ̃) .
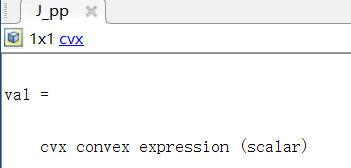
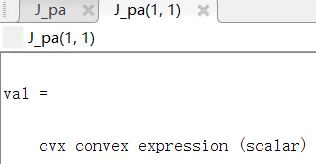
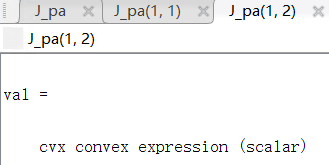
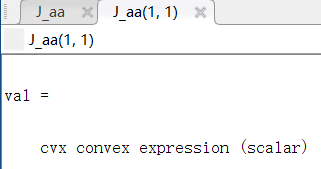
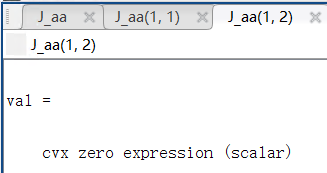

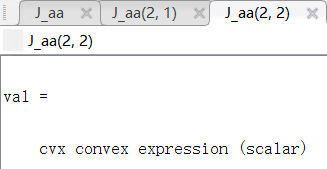
And U is
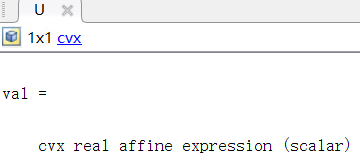
My variable declaration is as follows:

When performing the program on line 41 to make S must be a positive semidefinite matrix, the following error prompt will be generated:


Note: the function square_pos( norm(A*T,‘fro’) ) is used to generate the J_pp, J_pa and J_aa. Thus, J_pp, J_pa and J_aa are all cvx convex expression. Where A is given matrix.
And I know the reason for this error is that both sides of the equal sign must be affine.
So, Is there any way to solve this problem?