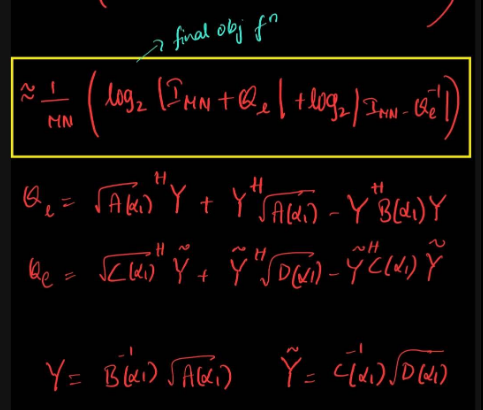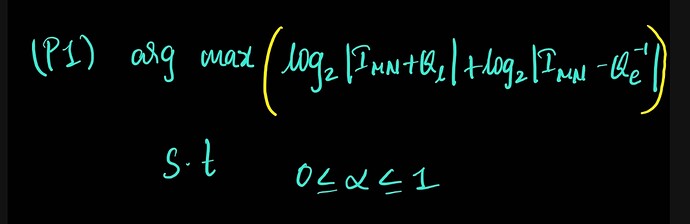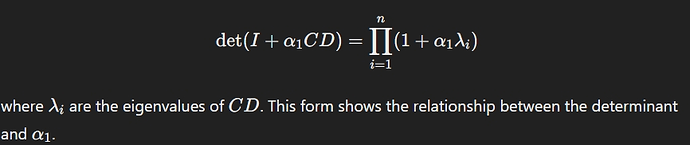cvx_begin quiet
variable alpha1
expression QL
QL=(sqrt(alpha1*real(A_MAT))'*Y_MAT)+(Y_MAT'*sqrt(alpha1*real(A_MAT)))-(Y_MAT'*((alpha1^2)*B_MAT)*Y_MAT)+(sqrt(alpha1*imag(A_MAT))'*Y_MAT)+(Y_MAT'*sqrt(alpha1*imag(A_MAT)))-(Y_MAT'*((alpha1^2)*B_MAT)*Y_MAT);
obj=log2(det(eye(M*N)+QL));
maximize obj
subject to
0<=alpha_1<=1;
cvx_end;
I am getting the above error while maximizing log2(det()), kindly HELP!!
Where in the CVX documentation to use see the function det which can take a CVX argument? There is none.
You can use log_det or det_rootn if the argument is psd and (I believe, even though not documented) concave (or affine), and constructed following CVX"s rules. I don’t know what your input data is, so I don’t know whether it satisfies the needed conditions.
Please carefully read
and re-read the CVX Users’ Guide.
Thanks a lot for your quick response, can you tell me if this problem can be solved using CVX or not?
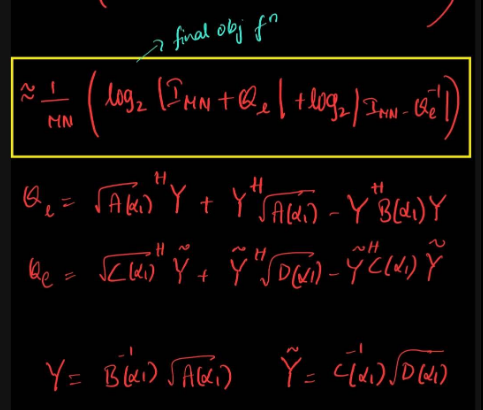
where the matrices(Ql,A,B,Y) are complex and the constraint is 0 \leq \alpha_1 \leq 1. Thank you
I have no idea what any of that stuff is. You don’t even show an optimization problem.
Your first task is to determine whether your problem, whatever that is (and I don’t know), s a convex optimization problem. You would know you need to do that from reading the link in my preceding post.
Really sorry for not mentioning the actual problem statement, the matrices QL and QE here are complex and functions of the parameter \alpha_1, the first term log_det(I+QL) is concave increasing function where as the second term log_det(I-inv(QE)) is concave decreasing function , The matrix QL is a Hermitian positive semi definite matrix and QE is a Hermitian positive definite matrix. Can you confirm if we can maximize this objective function using cvx for the mentioned constraints
I still don’t know what QL or QE are in terms of the variable \alpha. As the link makes clear, it is incumbent on you to prove the objective is concave. Your statement claiming that is not sufficient. There have been many false claims of convexity (or concavity) on this forum.
Thank you once again, if we consider only the first term, the expression is concave if we consider the 1-D case
% Symmetrize QL to ensure it is symmetric
QL_sym = alpha1 *((QL + QL’) / 2);
% Objective function
obj = log_det(eye(M*N) + QL_sym);
% Maximize the objective function
maximize(obj)
subject to
0.5 <= alpha1 <= 1;
cvx_end
log(1+x) is concave in x in 1D, which doesn’t say anything about your problem.
I still have no idea what QL is as a function of the optimization variables.
You haven’t shown a complete program, so I have no idea what you’ve run. if you omit quiet, you will see the CVX and solver output, including what CVX says the final solution status is.
QL=alpha1*QL_sym, where QL_sym is a symmetric matrix. This is shown in the command window after omitting quiet
I still have no idea what your program is, because you haven’t shown a complete program. I have no idea what your convex optimization problem is, because you haven’t shown clearly what it is.
The output you show says the problem is unbounded. Therefore, any variable values after cvx_end are meaningless.
if all you show is bits and pieces, i will not know what you ran, and not be able to help you.
You should show a complete MATLAB session, with the output you obtained, which should be the output for that program (not for some other version of something you once ran)…
This is my complete matlab code
tic
clc;
clear variables;
alpha_1=0.5;
alpha2=1-alpha_1;
[F_M,F_N,H_eff_R,H_RAN_eff,M,N,Nr,Nt,H0]= MIMO_OTFS_RIS_Channel();
[H_eff_E]= Eaves_MIMO_RIS_channel();
Q=H_eff_R'*inv(H_eff_R*H_eff_R')*H_eff_R;
T_op=eye(size(Q))-Q;
n=(1/sqrt(2)) * (randn(Nt*M*N, 1) + 1j*randn(Nt*M*N,1));
U=4;
SNRDB =20;
SNR=10.^(SNRDB/10);
sigma_IRS_2 = 1;
Pt=SNR;
n_legit=kron(eye(Nr),kron(F_N,eye(M)))*sigma_IRS_2*(1/sqrt(2)) * (randn(Nr*M*N, 1) + 1j*randn(Nr*M*N,1)); % Noise at Rxr for IRS with optimised phase
n_eaves=kron(eye(Nr),kron(F_N,eye(M)))*sigma_IRS_2*(1/sqrt(2)) * (randn(Nr*M*N, 1) + 1j*randn(Nr*M*N,1)); % Noise at Rxr for IRS with optimised phase
n_power=mean(abs(n_legit).^2);
np_eaves=mean(abs(n_eaves).^2);
A=H_eff_R'*H_eff_R;
B=((n_power)/(alpha_1*Pt)*eye(Nt*M*N))+((alpha2/alpha_1)*(H_eff_E'*H_eff_E));
[W, Lambda] = eig(inv(B)*A);
O=gallery('orthog',M*N);
V_SLNR=W(:,1:M*N)*O;
Rn=eye(Nr*M*N);
G1=alpha_1*Pt*V_SLNR'*H_eff_R'*inv((H_eff_R*(V_SLNR*V_SLNR')*H_eff_R')+Rn);%MMSE Combiner,inv of NrMN
A_MAT=G1*H_eff_R*(V_SLNR*V_SLNR')*H_eff_R'*G1';
B_MAT=(n_power*(G1*G1'));
% Compute QL
QL = inv(B_MAT) * A_MAT;
cvx_begin
variable alpha1
expression QL_sym
% Symmetrize QL to ensure it is symmetric
QL_sym = alpha1 *((QL + QL') / 2);
% % Objective function
obj1 = log_det(eye(M*N)+QL_sym);
maximize(obj1)
subject to
0<=alpha1 <= 1;
cvx_end
toc
and this is my optimization problem
arg max log_det(eye(MN)+\alpha1inv(B_MAT)*(A_MAT))
subject to
0<=alpha1<=1.
When I changed the constraint 0.5<=alpha1<=1 , Im still getting optimized \alpha_1 close to zero(10^-3 order). Kindly help me resolve this
You have not provided various functions you called; Therefore your problem is not reproducible.
Have you looked at the eigenvalues of (QL + QL') / 2). What are the min and max of the eigenvalues? What are the min and max of the eigenvalues of eye(M*N)+ (QL + QL') / 2 ?
Unless the CVX status is Solved or Inaccurate/Solved, all variable values are meaningless.
Also, if you have Mosek available as solver, use it. And pay attention to any warnings it might issue.
Should I share those functions here?
The min eigen value of the matrix QL+Ql’/2 is 5.9749 and max eigen value is 59.7322
The min eigen value of the matrix eye(M*N)+ (QL + QL') / 2 is 6.9749 and max eigen value is 60.7322, which means both are positive definite matrices.
Can you elaborate on the mosek solver part?
Use of Mosek will avoid the use of CVX’s unreliable Successive Approximation method for dealing with exponential cone related functions, including log_det. It also provides better warnings and other diagnostic information. And Mosek developers read this forum and can provide more insight on Mosek solver logs.
I used the following property of matrices
I don’t see how you’d make use of that in CVX.
lambda = real(eig(inv(B_MAT) * A_MAT));
cvx_begin
variable alpha1
maximize(sum(log2(1 + alpha1 * lambda)));
subject to
0 <= alpha1 <= 1
cvx_end
I was able to solve using that property, but when I extend the objective function as
maximize(sum(log2(1 + alpha1 * lambda))+ sum(log2(1 - lambda_e *alpha1^-1))) where lambda_e = real(eig((inv(D_MAT) * C_MAT))); I am getting the following error
Error using recip
Disciplined convex programming error:
Invalid operation: 1 / {real affine}
Fro alpha >= lambda_e, there’s a formulation of the 2nd log term as a concave expression, listed in 5.2.10 Other simple sets of the Mosek Modeling Cookbook. Changes are needed to account for the differences in convention (definition) used by Mosek vs. CVX for rotated 2nd order cone and exponential cone.
You can do the following in CVX, which is easier in CVX than the Mosek formulation:
log2(1-lambda/alpha1) can be reformulated as
log(1-lambda*inv_pos(alpha1))/log(2)
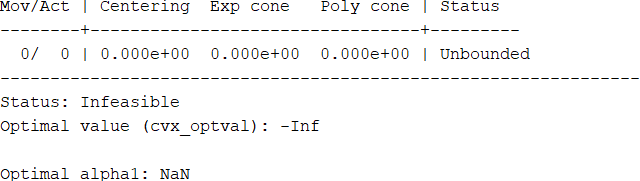
This is the status in the command window after modifying the objective function like you said
