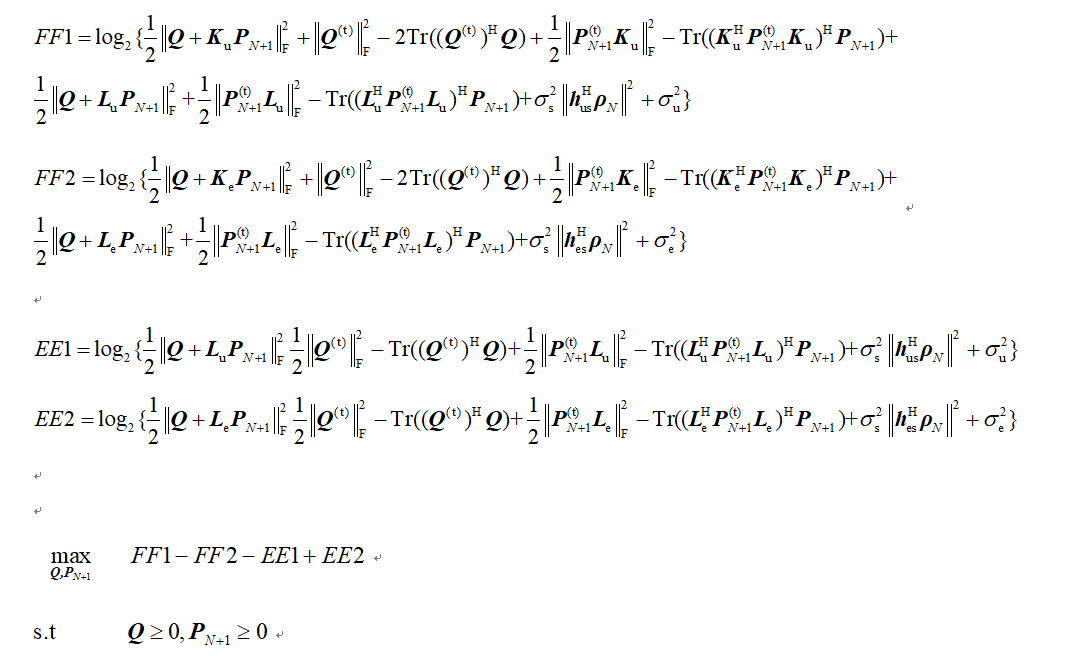Part of my code shows in the picture ,Ku is constant,Q and PN1 are matrix variables,where Q is complex semidefinite matrix and PN1 is real positive semidefinite matrix,both of them are N+1 - dimensional matrix. I’ve tried to find the problem via CVX Users’ Guide but failed to get relevant examples.
What do you intend to do with a.? Is the overall optimization problem convex?
And in the future, please copy and paste your code, using the Preformatted text icon, rather than posting an image of your code.
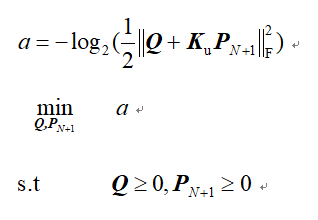
Sorry for my non - standard behavior,my question is in the picture and here is my code
cvx_begin
variable Q(N+1,N+1) complex semidefinite
variable PN1(N+1,N+1) semidefinite
a=-log(square_pos(norm(Q+Ku*PN1,'fro')))/log(2);
minimize a
subject to
Q >= 0;
PN1 >= 0;
cvx_endPlease show us your proof that a is convex.
That has zero chance of being convex because you are essentially maximizing a norm. And that is a nonconvex problem.
I believe @Erling is correct. The log,`and even the squaring can be eliminated due to being monotonic, which leaves the the objective function as minimizing the Frobenius norm of an affine function of the variables. Hence the objective is concave. rendering this a Concave Programming problem. Indeed, a difficult non-convex nonlinear SDP.
Your only hope for solving this to global optimality, and perhaps only if the dimension is small enough, is to use YALMIP’s BMIBNB global solver under YALMIP.
Actually, if there are no other constraints, this problem is unbounded. Regardless of what K is, P can be set to the zero matrix, and for example, Q(1,1) can be increased to \infty, with its other elements at zero, resulting in the objective going to -\infty.
Thank you for your reply.The method i referred is paper "Power-Efficient Resource Allocation for Multiuser MISO Systems via Intelligent Reflecting Surfaces “,in page 3 Number (11).As he said the question is in form of a difference of convex (d.c.) functions and problem is jointly convex with respect to the optimization variables and then he apply CVX to solve the problem. The only difference is i have the"log2” outside the matrix Frobenius norm. Due to other part of the problem ,it’s difficult to change “log2” into exponential form.
The formulation you show does not appear in that paper https://arxiv.org/pdf/2005.06703.pdf .
As @Erling and I essentially said, the log can be removed from the objective, due to its being monotonic. Doing that, the 'revised" a is only the first of 3 terms in the constraint (11), And that a appears without minus (I presume \gamma_j is nonnegative) and is the only convex portion of the constraint. Somehow, you have made it the objective, and crucially, inserted a minus sign. That minus sign is why @Erling and I concluded it is non-convex.
You need to go back to the “drawing board” and rethink what you are doing.
Thank you for your advice.picture above is the whole point of the problem,all but two variables"Q,PN+1" are known constants. The problem i meet in my objective is similar to the paper "Power-Efficient Resource Allocation for Multiuser MISO Systems via Intelligent Reflecting Surfaces “in the constraint (11). But there are many logarithms added and subtracted in my objective,removing “log” will pay a high price.So is there any method that i can keep the above format and use CVX to solve the problem without mistake?
That doesn’t look convex. Coming up with an iterative scheme which would solve this by some iterative sequence of convex problems sounds like a research problem, which may not be likely to succeed, and is out of scope of this forum.
There may not be any solver in existence which can handle this, except for very low dimension.
ok,i will try other methods,thanks again
Do you have proof that the problem is convex.
Usually be inspecting the proof is a good starting point for figuring out a DCP compliant formulation if it is possible.