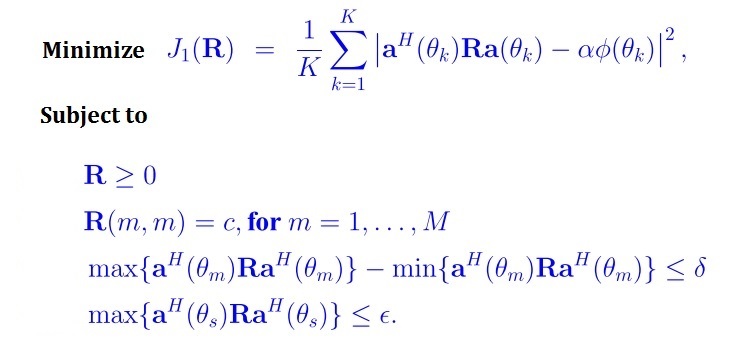Disciplined convex programming error: Cannot perform the operation norm( {convex}, 2 )

1

cvx_precision high
cvx_begin
variable R(M_T, M_T) semidefinite
for i = 1 : K
Designed_beam(i) = E_theta1(:,i)'RE_theta1(:,i);
end
cost_func = norm(abs(Designed_beam - phi),2)

minimize(cost_func)
subject to
for i = 1 :M_T
R(i,i) == C/M_T;
end
cvx_end

2

I don’t think you need abs in your code for cost_func. But I think it would be accepted by CVX 3.0 . But don’t quote me on that, ha ha, in case I’m wrong.

Alternatively, you could use
cost_func = sum_square(Designed_beam - phi)
or if it’s really complex, although I don’t see your declarations, use sum_square_abs . These latter forms match your original displayed math. Given that there is only one term (the norm or sum of squares), they should have identical argmins.

3

12.jpg730×341 40.9 KB

4

a(theta_k) is a known vector
\alpha is a constant
c is a constant
the only variable here is the matrix R which is semi-definite square matrix

5

Error using cvx/sum_square (line 7)
Disciplined convex programming error:
The argument to SUM_SQUARE must be real and affine.

Error in Beampattern_design (line 48)
cost_func = sum_square(Designed_beam - phi)

6

I made up some input data in the first line, and then ran the following in CVX Version 2.1 Build 1117.

>> K=3; M_T=3; E_theta1=randn(3); phi=2;
>> cvx_begin
>> variable R(M_T, M_T) semidefinite
>> for i = 1 : K
>> Designed_beam(i) = E_theta1(:,i)'*R*E_theta1(:,i);
>> end
>> cost_func = sum_square(Designed_beam - phi)
cost_func =
    cvx convex expression (scalar)

Does this work for you? If so, what is the difference between this and what you ran which resulted in the error message?

Note that removing the semicolon from
Designed_beam(i) = E_theta1(:,i)'*R*E_theta1(:,i)
produces the output

Designed_beam =
    cvx real affine expression (scalar)
Designed_beam =
    cvx real affine expression (1x2 vector)
Designed_beam =
    cvx real affine expression (1x3 vector)

So why isn’t your Designed_beam - phi real and affine?

8

Running this, I get

Designed_beam =
    cvx mixed real affine/complex affine expression (1x181 vector)

Use sum_sq_abs (because you have some complex data)
>> cost_func = sum_square_abs(Designed_beam - phi)

cost_func =
    cvx convex expression (scalar)
9

Thank you so much;
I really appreciate your efforts

10

Final question
how to implement the max and min functions in the original optimization problem.

11

It looks to me like you can just enter this straightforwardly. Have you tried it?

help cvx/max
    Disciplined convex/geometric programming information:
        max is convex, log-log-convex, and nondecreasing in its first 
        two arguments. Thus when used in disciplined convex programs, 
        both arguments must be convex (or affine). In disciplined 
        geometric programs, both arguments must be log-convex/affine.
12

I added these lines of code
max(Designed_beam(36:46)) - min(Designed_beam(36:46)) <= 23
max(Designed_beam(136:146)) - min(Designed_beam(136:146)) <= 23
max(Designed_beam(1:35)) <= 1
max(Designed_beam(47:135)) <= 1
max(Designed_beam(147:181)) <= 1

it gives me a similar error

Error using cvx/max (line 209)
Disciplined convex programming error:
Invalid computation: max( {complex affine} )

13

Hmm, maybe there is roundoff level imaginary component of Designed_beam.

max(real(Designed_beam(36:46))) - min(real(Designed_beam(36:46))) <= 23

should work.

14

it works, but gives non accurate values. and all elements of R are NaN

15

Show us your complete program, with all input data, and the output when you run it.

Did you get

Status: Infeasible
Optimal value (cvx_optval): +Inf

In such case, all elements of R would be NaN.

16

Status: Infeasible
Optimal value (cvx_optval): +Inf

R_noNull =

NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN
NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN
NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN
NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN
NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN
NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN
NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN
NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN
NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN
NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN

17

global phi
M_T = 10;
K = 181;
k1 = -55;
k2 = -45;
k3 = 45;
k4 = 55;

phi = zeros (1 ,K);
for i4 = k1 + 91: k2 + 91
phi (i4) = 25;
end
for i4 = k3 + 91: k4 + 91
phi (i4) = 25;
end
phi ;
C = 0.62;
for k = 1:K
Theta_2(k) = ( pi /180) * ( k - 91);
Theta_3(k) = (k - 91);
E_theta1(:,k) = [
1 exp(i1pisin(Theta_2(k))) exp(i2pisin(Theta_2(k))) exp(i3pisin(Theta_2(k)))…
exp(i4pisin(Theta_2(k))) exp(i5pisin(Theta_2(k))) exp(i6pisin(Theta_2(k))) exp(i7pisin(Theta_2(k)))…
exp(i8pisin(Theta_2(k))) exp(i9pi*sin(Theta_2(k)))
];
%Designed_BeamPattern(k) = E_theta1(:,k)'R_noNullE_theta1(:,k);
end
cvx_precision high
cvx_begin
variable R(M_T, M_T) semidefinite
for i = 1 : K
Designed_beam(i) = E_theta1(:,i)'RE_theta1(:,i);
end
cost_func = sum_square_abs(Designed_beam - phi);
minimize(cost_func)
subject to
max(real(Designed_beam(36:46)))- min(real(Designed_beam(36:46))) <= 20
max(real(Designed_beam(136:146))) - min(real(Designed_beam(136:146))) <= 20
max(real(Designed_beam(1:35))) <= 2
max(real(Designed_beam(47:135))) <= 2
max(real(Designed_beam(147:181))) <= 2
for i = 1 :M_T
R(i,i) == C;
end
cvx_end

18

Your problem is infeasible.

I removed

for i = 1 :M_T
R(i,i) == C;
end

and an optimal solution was found.

By the way,
diag(R) == C
would have been a more compact way of imposing your constraints

for i = 1 :M_T
R(i,i) == C;
end
1 Like
19

Thank you so much
I appreciate all your efforts