Disciplined convex programming error: Cannot maximize a(n) convex expression

Nonconvex
1

Here is my problem:
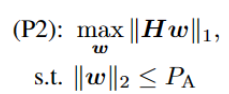
image
where H is a N×M complex matrix, each element of H has an amplitude of 0 ~ 1 and a phase of 0 ~ 2π. w is a M ×1 complex variable. PA denotes power (I set PA to 10 in the simulation).
Here is my code:
cvx_begin sdp
variable w(M,1) complex;
maximize (norm(H * w,1))
subject to
norm(w,2) <= PA;
cvx_end
when I run my code, there is a problem: Disciplined convex programming error: Cannot maximize a(n) convex expression. How can I solve the problem?

2

Because it is non-convex, you can solve it with something other than CVX. For instance, YALMIP.

3

Thanks for your reply!

4

Hi,

Although all C_et and C_er are hermitian semidefinite positive, the below gives me it is not convex, and I have no idea why!

              cvx_begin quiet
             cvx_solver Mosek

                  variable W(M,2*K) complex ;
                  Objective = 0;
                  for q=1:K 
                      Objective = Objective + (W(:,q)'*C_et(:,:,q)* W(:,q)) + (W(:,K + q)'*C_er(:,:,q)* W(:,K + q));
                  end

                  maximize Objective ;
                  subject to
                  square_pos(norm(W,'fro')) <= 1;

              cvx_end

Error using cvxprob/newobj (line 57)
Disciplined convex programming error:
Cannot maximize a(n) convex expression.

Error in maximize (line 21)
newobj( prob, ‘maximize’, x );

Error in Channel_4 (line 143)
maximize Objective ;

5

The objective is convex quadratic. Minimizing it would be convex, but maximizing it is not convex.

Perhaps you should bone up on convex optimization. Convex Optimization – Boyd and Vandenberghe .

6

Thanks for your reply!