"cvx_status--unbounded cvx_optval--+Inf"

1

Dear everyone,
Does cvx can’t solve two related variables simultaneously?
I thought it was the problem and then I set another variable as given one using AO algorithm.
here’s my code.

function [Fi_opt,flag] = Generate_ES_Fi(N, M, K, H, G,...  
          W_ini, Fi_ini_ES, noise_maxpower, trans_maxpower)

cvx_begin %quiet
variable Fi(2,M) complex
%variable FI(M,M,K) hermitian
variable relax_scaler_D1(M,M,K) hermitian semidefinite
variable relax_scaler_D2(M,M,K) hermitian semidefinite

expressions    LMI(M+M+1,M+M+1,K)

W=W_ini;  
k=1:1:K;
u=K:-1:1;
 for i=1:length(k)
    if k(i)==1||u(i)==1  
    a(k(i))=0.5;
%%%%%  Generate LMI %%%%%
     LMI(M+M+1,M+M+1,K);
     LMI(:,:,k(i))=[relax_scaler_D1(:,:,k(i)), FI(:,:,k(i)), Fi(k(i),:)';...
                FI(:,:,k(i))', relax_scaler_D2(:,:,k(i)) ,Fi(k(i),:)';...
               Fi(k(i),:), Fi(k(i),:) ,1 ];
         
     Ty(k(i))=trace(relax_scaler_D1(k(i)))-2*trace(Fi(k(i),:)'*Fi_ini_ES(k(i),:))+trace(Fi_ini_ES(k(i),:)'*Fi_ini_ES(k(i),:));
       end
end 
     maximize sum(a.*POLY)

     subject to
         k=1:K;
         u=K:-1:1;
     for i=1:length(k)
        if k(i)==1 || u(i)==1 
         
 %              diag(FI(:,:,u(i))+FI(:,:,k(i)))==1;
         LMI(:,:,k(i)) == hermitian_semidefinite(2*M+1);
         real(Ty(k(i)))<=0;
         real(relax_scaler_D1(:,:,k(i)))>=0;
         real(relax_scaler_D2(:,:,k(i)))>=0;
         %z(k)>=noise_maxpower;
     end
end
cvx_end

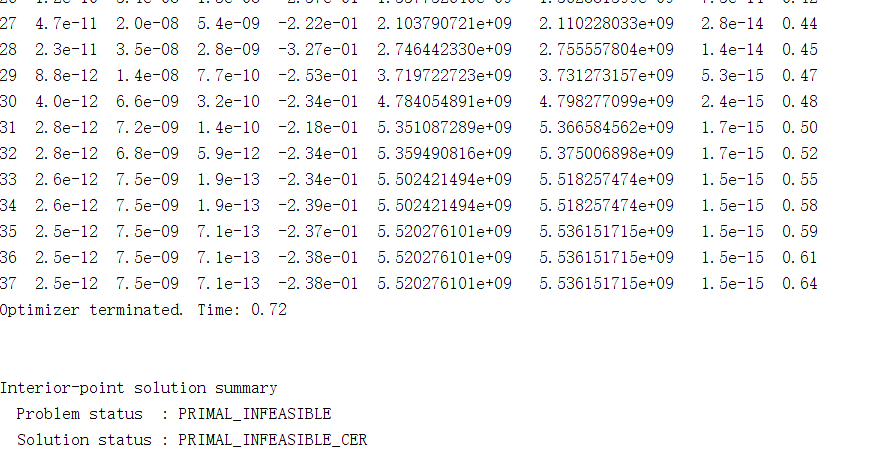
The results turns out:

image
image882×527 10.9 KB

The objective function is convex,the problem might be constrains.
I tried to eliminate variables to find out but failed.
Please someone give me a guide! gratefully thanks.

2

I have no idea whether your code is correct, because I don’t know what optimization problem you are trying to solve. Nor is your problem reproducible, because you have nor provided input data.

Nevertheless, try following the advice in https://yalmip.github.io/debuggingunbounded .

One thing you might try to do is start with a simpler, easier to understand model, get that working correctly, and then build up to the model you really want to solve.

3

So cvx can’t solve two variables?
I’m a beginner of cvx toolbox, what is the meaning of the results it shows?

4

input data :

 close all;
 clear all;clc;
 warning('off');

 %% Parameters Initialization 
                  
  N          = [3,6,6,10];            % array number of BS
  M          = [10,10,20,30];            % array number of STAR-RIS
  K          = 2;            % number of users
  SNR_dB     = 10;     % dBW
  %%%%% noise
  N0=10^((-174-30) / 10); %-174dBm
  B=10^7; %10MHz
  % noise_maxpower_original   = N0*B;            % % W
  noise_maxpower_original   = 10^((-80-30) / 10);
  power_max_dBm=10;
 %% Simulation loop %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
  num_loop = 10; 
  load('H_du_all');
  load('G_ru_all');
  % for i_p     = 1 : length(rate_min_dB)
  %Rate=zeros(K,length(rate_min_dB),100);
  for loop = 1 : num_loop 
      outerflag=1;   
      T1=cputime;          
      H=H_du_all(1:N,1:K,loop)/sqrt(noise_maxpower_original);%信道归一化
      G=G_ru_all(1:M,1:N,1:K,loop)/sqrt(noise_maxpower_original);
      noise_maxpower=1;
      %%  For different       %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
  fprintf('  loop | N | M | iteration \n');
for i_p     = 1 : length(N)

t0=cputime;
trans_maxpower=100 ;%trans_maxpower_all(i_p);
N=N(i_p);
M=M(i_p);
%%%%%  Initialize W and fi beamforming  %%%%%
%power_max=power_max_dBm(i_p);
a=0;b=2*pi;

%%%%%  Initialize Fi for different mode(ES,MS and TS )  %%%%%
Fi_temp=(b-a).*rand(2,M(i_p)) + sqrt(-1)*(b-a).*rand(2,M(i_p));
Fi_amp=rand(2,M(i_p));
Fi_ini_ES=Fi_amp.*exp(1j*angle(Fi_temp));
Fi_ini_eES=0.5*exp(1j*angle(Fi_temp));


W_ini=randn(N(i_p),K)*sqrt(trans_maxpower/(N(i_p)*K));
W(:,:,1)=full(W_ini);
Fi1(:,:,1)=full(Fi_ini_ES);%ESmode下的Fi迭代值
Fi2(:,:,1)=full(Fi_ini_eES);%equalESmode下Fi的迭代值


%disp('Proposed algorithm')
num_iterative = 20;
for n  = 1 : num_iterative
   %%%%%  Optimize W  %%%%%
    [W_1,rate_inf,flag_W] = Generate_ESMS_W(N, M, K, H, G,...  
          W(:,:,n), Fi1(:,:,n), noise_maxpower, trans_maxpower);
      %F_1,power_sub,innerflag
    W(:,:,n+1)=W_1;
    rate(n+1)=rate_inf;
    if flag_W==0 
        outerflag=0;
        break;
    end  
    %%%%%  Optimize fi  %%%%%
    [Fi_1,flag_Fi] = Generate_ES_Fi(N, M, K, H, G,...  
          W_ini, Fi1(:,:,n), noise_maxpower, trans_maxpower);
    Fi1(:,:,n+1)=Fi_1;
    %FiE(:,n+1)=FiE_opt;
    if flag_Fi==0
       outerflag=0;
        break;
    end  
     %%%%%  stop criterion  %%%%%
    fprintf('   %g  |  %g  |  %g  |  %g  \n',loop, N(i_p), M(i_p), n)
    if abs(rate(n+1)-rate(n))<10^(-3) %精度为10^(-3) 
        break;
    end
    SumRate(loop,t,n)=rate_inf;
 end
    if outerflag==0
        break;
    end
end
 end
5

CVX can handle any number of variables, unless it or the solver it calls runs out of memory.

You need to improve the scaling of the input data so that all non-zero input data is within a small number of orders of magnitude of one. Change the units to accomplish that. Otherwise you’ll cause havoc and unreliability in the solver.

6

I have changed the initial value of all variables within magnitude of 1.
and It still unbounded.
but the results indicate the problem might be convergence.

image
image873×450 12.9 KB

7

iteration 33-37 didn’t change value. does it mean convergence?

8

The solver, Mosek, reported the problem is primal infeasible. But presumably, Mosek was provided the dual by CVX, so this corresponds to your original problem (primal) being unbounded.

Please show all the solver and CVX output. Did Mosek issue any warnings about data being large or nearly zero? If the numerics are good, and Mosek didn’t issue any warnings, then you should follow the advice in the link in my first post. Try removing the objective and see what happens. Try with the objective, but placing finite lower and upper bounds on all variables, and see which variables end up on a bound at the optimal solution.

9

You cut the log output off just where it would get interesting: the residuals would indicate how good the certificate is. Maybe check that and consult https://docs.mosek.com/latest/toolbox/debugging-log.html#solution-summary

The huge objective value may indicate problems with convergence. Ie. it may be that your original problem has an optimal solution but it is so far away it is practically unbounded. That’s just a guess.

10

Thank you so much ,Mark.
I have handled this problem by restraining initial variables.And for god’s sake,it outputs the correct answer.

*** convert ublk to linear blk

SDPT3: homogeneous self-dual path-following algorithms

version predcorr gam expon
NT 1 0.000 1
it pstep dstep pinfeas dinfeas gap mean(obj) cputime kap tau theta

0|0.000|0.000|1.8e+01|1.8e+01|2.7e+07| 9.786892e+05| 0:0:00|2.7e+07|1.0e+00|1.0e+00| chol 1 1
1|0.040|0.040|1.8e+01|1.8e+01|2.8e+07| 9.767393e+05| 0:0:00|2.7e+07|9.8e-01|9.8e-01| chol 1 1
2|0.213|0.213|1.8e+01|1.8e+01|3.3e+07| 9.572414e+05| 0:0:00|2.4e+07|9.0e-01|8.7e-01| chol 1 1
3|0.444|0.444|1.6e+01|1.6e+01|4.1e+07| 8.690131e+05| 0:0:00|1.7e+07|7.5e-01|6.6e-01| chol 1 1
4|0.766|0.766|1.3e+01|1.3e+01|5.2e+07| 8.844922e+05| 0:0:00|8.4e+06|5.6e-01|3.9e-01| chol 1 1
5|0.881|0.881|3.8e+00|3.9e+00|1.5e+07| 4.651921e+05| 0:0:00|3.9e+05|6.1e-01|1.3e-01| chol 1 1
6|0.600|0.600|1.4e+00|1.5e+00|3.9e+06| 2.299754e+05| 0:0:00|1.8e+04|8.6e-01|6.8e-02| chol 1 1
7|0.871|0.871|1.6e-01|1.7e-01|2.9e+05| 4.785535e+04| 0:0:00|4.6e+03|1.3e+00|1.1e-02| chol 1 1
8|0.803|0.803|6.7e-02|6.7e-02|1.4e+05| 1.515200e+04| 0:0:00|2.0e+03|1.3e+00|4.6e-03| chol 1 1
9|0.827|0.827|1.3e-02|1.3e-02|2.4e+04|-1.022487e+01| 0:0:00|6.7e+02|1.4e+00|9.7e-04| chol 1 1
10|0.688|0.688|6.5e-03|6.6e-03|1.2e+04|-1.896650e+02| 0:0:00|2.4e+02|1.5e+00|5.3e-04| chol 1 1
11|0.960|0.960|1.9e-03|1.9e-03|3.7e+03|-1.071202e+03| 0:0:00|4.8e+01|1.6e+00|1.7e-04| chol 1 1
12|1.000|1.000|5.7e-04|6.0e-04|1.1e+03|-1.130560e+03| 0:0:00|1.9e+01|1.7e+00|5.4e-05| chol 1 1
13|0.951|0.951|1.2e-04|1.5e-04|2.2e+02|-1.164479e+03| 0:0:00|6.8e+00|1.8e+00|1.2e-05| chol 1 1
14|1.000|1.000|4.8e-05|7.5e-05|8.7e+01|-1.163957e+03| 0:0:00|1.4e+00|1.8e+00|4.8e-06| chol 1 1
15|0.919|0.919|9.8e-06|3.8e-05|1.7e+01|-1.162376e+03| 0:0:00|6.3e-01|1.8e+00|9.8e-07| chol 1 1
16|1.000|1.000|2.7e-06|2.7e-05|4.5e+00|-1.162035e+03| 0:0:00|1.1e-01|1.8e+00|2.7e-07| chol 1 1
17|0.894|0.894|4.9e-07|1.4e-05|7.6e-01|-1.162088e+03| 0:0:00|3.9e-02|1.8e+00|4.9e-08| chol 1 1
18|1.000|1.000|1.2e-07|6.3e-06|2.0e-01|-1.162207e+03| 0:0:00|5.1e-03|1.8e+00|1.3e-08| chol 1 1
19|0.928|0.928|1.7e-08|3.3e-06|2.6e-02|-1.162253e+03| 0:0:00|1.6e-03|1.8e+00|1.7e-09| chol 1 1
20|0.992|0.992|2.9e-09|1.4e-06|4.6e-03|-1.162285e+03| 0:0:00|1.9e-04|1.8e+00|2.9e-10| chol 1 1
21|0.983|0.983|2.7e-10|6.3e-07|4.2e-04|-1.162299e+03| 0:0:00|3.4e-05|1.8e+00|2.7e-11| chol 1 1
22|0.983|0.983|3.3e-10|2.7e-08|1.5e-05|-1.162313e+03| 0:0:00|3.4e-06|1.8e+00|9.6e-13| chol 1 1
23|0.990|0.990|4.1e-10|7.3e-10|5.6e-07|-1.162314e+03| 0:0:00|1.5e-07|1.8e+00|0.0e+00|
Stop: max(relative gap,infeasibilities) < 1.49e-08

number of iterations = 23
primal objective value = -1.16231399e+03
dual objective value = -1.16231395e+03
gap := trace(XZ) = 5.60e-07
relative gap = 4.81e-10
actual relative gap = -1.73e-08
rel. primal infeas = 4.05e-10
rel. dual infeas = 7.27e-10
norm(X), norm(y), norm(Z) = 3.1e+03, 9.1e+02, 1.0e+03
norm(A), norm(b), norm© = 2.5e+03, 1.0e+03, 3.4e+02
Total CPU time (secs) = 0.37
CPU time per iteration = 0.02
termination code = 0
DIMACS: 4.1e-10 0.0e+00 7.3e-10 0.0e+00 -1.7e-08 2.4e-10

Status: Solved
Optimal value (cvx_optval): +2333.86

Calling SDPT3 4.0: 248 variables, 116 equality constraints