CVX status='solved' but the results not meet my constraint

1

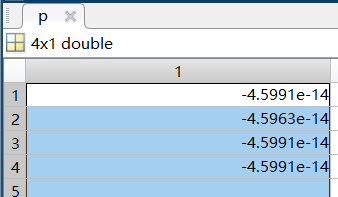
I used dichotomy to approximate f_n(k,s), who should be in the range between 'F_max' and 'F_min', i.e. between 100 and 0.01. But due to the process, the cvx variable p went negative and did not satisfy one of my constraints p(k)＞0, making the value of f_n(k,s) worth to 10^5

Is there something wrong with my code? Why does it go negative when it’s clearly restricted to p(k)＞0

while F_max - F_min > convergence_factor %convergence_factor = 0.01;
    F_next = (F_max +F_min) / 2;

cvx_begin quiet
variable p(K,1)
expression f_n(K,M)
expression f_n_part1(K,M)

for s = 1:M
for k = 1:K
        f_n_part1(k,s)=0;
        for i = 1:K
            for m = 1:M
                if i == k && m==s                   
                       f_n_part1(k,s) = f_n_part1(k,s) + 0;
                else
                  
                       f_n_part1(k,s) = f_n_part1(k,s) + p(i)*(abs(weight_n(:,k,s)'*dki(:,k,i,s,m)))^2;
                end
            end
        end
    f_n(k,s) = a_bar(k,s) - (p_n(k)*(abs(weight_n(:,k,s)'*b(:,k)))^2) * inv_pos(2 * real(sqrt(p_n(k))*(weight_n(:,k,s)'*b(:,k))'*(weight_n(:,k,s)'*b(:,k))*sqrt(p(k))) - p_n(k)*(abs(weight_n(:,k,s)'*b(:,k)))^2)...
        - b_bar(k,s) * abs(weight_n(:,k,s)'*b(:,k))^2 * p(k)...
        - c_bar(k,s) * f_n_part1(k,s);  



end

end

f_last = 0;

    maximize (0)
   
    subject to

    for k = 1:K
        p(k) <= p_max; 
    end

    for k = 1:K
        p(k) >= 0;
    end
    
    for s = 1:M
        for k = 1:K
        f_n(k,s) >= F_next;
        end
    end
    
    for s = 1:M
        for k = 1:K
        2 * sqrt(p_n(k))*real((weight_n(:,k,s)'*b(:,k))'*(weight_n(:,k,s)'*b(:,k)) )*sqrt(p(k)) - p_n(k)*(abs(weight_n(:,k,s)'*b(:,k)))^2>= 0;%**eq(6)
        end
    end
    cvx_end

    %%
    if strfind(cvx_status,'Solved')
        F_min = F_next;
        p_final = p;
    else
        F_max = F_next;
    end
end
2

屏幕截图 2024-04-23 162604

3

p value of -4.6e-14 is within feasibility tolerance of satisfying the constraint; therefore it is considered by the solver and CVX to be feasible.

If you can’t tolerate such a value, change your constraint to something like p >= 1e-6

4

Thank you! I set p >= 1e-6 according to your advice. The problem is solved. :blush: