CVX status：infeasible，cvx_optval:-Inf,please help

[cool888-s]

hello,I now want to use this optimization problem to get the best W, but the result has always been infeasible. Excuse me, what’s wrong with this code？
this is the optimization problem

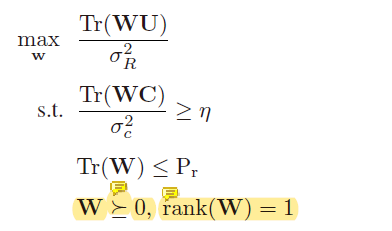
and this is my codes：

clc,clear,close all
M = 20;
Mx = 4;
Mz = 5;
Nx = 3;
Nz = 4;
N = Nx*Nz;
sigama_r = 0.1;
sigama_c = 0.1;
Pr = 3;
SNR_cu = 10^(22/10);

pos_bs = [0,2];
pos_ris = [100,2];
pos_cu = [100,1];

d_br = norm(pos_bs-pos_ris,2);
d_ru = norm(pos_ris-pos_cu,2);
d_bu = norm(pos_cu-pos_bs,2);
L = 3;

G = generate_channel_BR(Mx,Mz,Nx,Nz,L,d_br);
hd = generate_channel_BU(Mx,Mz,L,d_bu);
hr = generate_channel_RU(Nx,Nz,L,d_ru);
[A,B] = generate_AB(M,N);
V = diag(exp(1j*(rand(1,N)2pi)));

U1 = G’VA*V’*G+B;
U = U1’*U1;
C1 = hd’+hr’*V’*G;
C = C1’*C1;

cvx_begin sdp
variable W(M, M)
maximize(real(trace(WU))/sigama_r);
subject to
real(trace(WC))/sigama_c >= SNR_cu;
real(trace(W)) <= Pr;
W == hermitian_semidefinite(M);
cvx_end

This is the result of the operation：

Calling SDPT3 4.0: 402 variables, 192 equality constraints

num. of constraints = 192
dim. of sdp var = 40, num. of sdp blk = 1
dim. of linear var = 2

---

SDPT3: Infeasible path-following algorithms

---

version predcorr gam expon scale_data
HKM 1 0.000 1 0
it pstep dstep pinfeas dinfeas gap prim-obj dual-obj cputime

0|0.000|0.000|8.0e+02|5.4e+01|2.6e+06|-2.551829e+03 0.000000e+00| 0:0:00| chol 1 1
1|0.390|1.000|4.9e+02|5.0e-01|2.5e+06|-1.530119e+03 5.930304e+04| 0:0:00| chol 1 1
2|0.039|1.000|4.7e+02|2.5e-01|4.8e+06|-1.470490e+03 3.357927e+07| 0:0:00| chol 1 1
3|0.004|1.000|4.7e+02|1.2e-01|7.9e+08|-1.464534e+03 1.815630e+12| 0:0:00| chol 1 1
4|0.000|0.000|4.7e+02|1.2e-01|1.9e+10|-7.374155e+02 3.776397e+13| 0:0:00| chol 2 2
5|0.000|0.000|4.7e+02|1.2e-01|1.3e+11|-8.436520e+02 2.557190e+14| 0:0:00| chol 2 2
6|0.000|1.000|4.7e+02|1.5e-02|4.9e+17|-8.779422e+02 9.802866e+20| 0:0:00|
sqlp stop: primal problem is suspected of being infeasible

number of iterations = 6
residual of primal infeasibility
certificate (y,Z) = 2.00e-22
reldist to infeas. <= 4.11e-21
Total CPU time (secs) = 0.24
CPU time per iteration = 0.04
termination code = 1
DIMACS: 4.7e+02 0.0e+00 1.8e-02 0.0e+00 -1.0e+00 5.0e-04

---

Status: Infeasible
Optimal value (cvx_optval): -Inf

This is technically possible because I’m currently redoing the paper, but I don’t know what has been causing the problem. Could you take a look at it for me, Please

[Erling (Erling D.Andersen)]

The post below has suggestion for what to do:

How to deal with an issue using Cvx!

False claims of convexity (this forum is littered with them). Please carefully read before posting a request for help. Input data scaling: Check your input data for bad numerical scaling. All non-zero input data should be within s small number of orders of magnitude of 1; otherwise, the solver may encounter numerical difficulties or unreliability. Change the units used in order to accomplish this Solvers called by CVX use double precision: Solvers only satisfy constraints to within a feas…

[zal123]

Hi,Erling,
I want to know something about input data scaling. When some data have e-7 order of magnitudes while other data have e+07 order of magnitudes, do I still need to do the data scaling? Because when data is scaled too much, some features have been droped.

[Mark_L_Stone]

Input data varying from e-7 to e7 spans 14 orders of magnitude (digits), out of the approximately 16 digits available to a double precision solver. That is likely to result in numerical difficulties or unreliability.

We don’t know much about your problem. If there is not a way to scale your inputs such that they span a much smaller range, perhaps some of the features should be dropped? Or if all those features are really important to the problem, maybe you need a higher precision (for instance, quad precision) solver, of which there are some for certain types of problems, but not available under CVX.