CVX SDP infeasible solution

1

Hi,
I’m solving a CVX SDP problem, but it gives me infeasible solutions.
I’m sure that the problem is convex, and I have tried mosek,sedumi, sdpt3 and none of them works.
I know that the scaling is bad, I’ve tried to scale the value back to magnitude=1 but the solution is still infeasible, and I’m afraid that the scaling might make the problem another problem instead of the original problem.
Is there any advice that I can tried to solve thi problem ? I really appreciate it !
The details of my code is listed below, thanks for the help !

%%
clc;clear all;
%Initialization
%RSU location, transmit and receive antenna,P=30dBm
M=2;
RSU=[-30,30;30,30];
Nt=32;
Nr=32;
d=1/2; %antenna spacing distance
P=10^(30/10)10^-3; %power=30dBm
%Vehicle location , single antenna
K=2;
CAR=[-5,0;15,0];
%Sample (for estimation)
fc=110^9;
delta_f=0.110^9;
T=1/delta_f;
L=32;
Ts=T/L;
% CRLB Performance
gamma1=0.01;
gamma2=0.01;
% Outage Probability
eps1=0.05;
eps2=0.05;
%Parameter Initialization
c=310^10; %speed of light
rho=10+101i; %fading coefficient
SNR=25;
%sigma=sqrt((10^((0-SNR)/10))*10^(-3));
sigma_c=0.001;
sigma_r=0.0001;
%Radar and Signal Model Initialization

%% Input Estimated Paremeter
filename = [‘estimation_2RSU_2CAR’,‘.mat’];
load(['C:\Users\CCRG613\Desktop\CCRG\Working\RSU_ISAC\Work_Hard\2RSU_2CAR\Robust_beamforming\Estimation_Parameter',filename],‘AoA_estimated’,‘dis_estimated’,‘speed’);

ang_estimated=AoA_estimated;
%Reflection coeffcient & Delay
beta=zeros(M,K,M); %reflection coefficent
mu=zeros(M,K,M); %doppler frequency
beta_tilde=zeros(M,K,M);
for m=1:M
for k=1:K
for mm=1:M
beta(m,k,mm)=rho/(dis_estimated(m,k)+dis_estimated(mm,k));
mu(m,k,mm)=speed(k)*cos(ang_estimated(m,k))*fc/c+speed(k)cos(ang_estimated(mm,k))fc/c;
beta_tilde(m,k,mm)=beta(m,k,mm)exp(1i2pimu(m,k,mm)*Ts);
end
end
end
%% Robust Beamforming (Sum Rate)

h_CSI_hat=zeros(Nt,M,K);
zeta=2; %Path loss exponent
d_r=1;
for m=1:M
for k=1:K
h_CSI_hat(:,m,k)=sqrt(Nt/L)(dis_estimated(m,k)/d_r)^(-zeta)((1/sqrt(Nt))exp(-1i(0:Nt-1)'2pidcos(ang_estimated(m,k))));
end
end
C=zeros(Nt,M,K);
e=zeros(Nt,m,k);
a_par=zeros(Nt,M,K);
for m=1:M
for k=1:K
for nt=1:Nt
a_par(nt,m,k)=((1/sqrt(Nt))1i(nt-1)‘2pidsin(ang_estimated(m,k))exp(-1i(nt-1)‘2pidcos(ang_estimated(m,k))));
end
C(:,m,k)=sqrt(Nt/L)(dis_estimated(m,k)/d_r)^(-zeta)10^(-2)a_par(:,m,k);
e(:,m,k)=sqrt(Nt/L)10d_r^(zeta)(-zeta)dis_estimated(m,k)^(-zeta-1)((1/sqrt(Nt))exp(-1i(0:Nt-1)'2pidcos(ang_estimated(m,k))));
end
end
Sigma1=zeros(Nt,Nt,M,K);
for m=1:M
for k=1:K
Sigma1(:,:,m,k)=C(:,m,k)*C(:,m,k)’*gamma1+e(:,m,k)*e(:,m,k)’*gamma2;
end
end
%% Robust Beamforming (CRLB)

% Angle CRLB
q=zeros(M,K);
for m=1:M
for k=1:K
q(m,k)=1ipisin(ang_estimated(m,k));
end
end
u1=zeros(Nr,Nt,M,K);
u1_par=zeros(Nr,Nt,M,K);

u2=zeros(Nr,Nt,M,K,M);
u2_par_m=zeros(Nr,Nt,M,K,M);
u2_par_mprime=zeros(Nr,Nt,M,K,M);

b=zeros(Nr,1);
a=zeros(Nt,1);
for nr=1:Nr
b(nr)=nr-1;
for nt=1:Nt
a(nt)=nt-1;
for m=1:M
for k=1:K
u1(nr,nt,m,k)=(b(nr)+a(nt))exp(-1ipi*(b(nr)+a(nt))cos(ang_estimated(m,k)));
u1_par(nr,nt,m,k)=(b(nr)+a(nt))^2exp(-1ipi(b(nr)+a(nt))cos(ang_estimated(m,k)));
end
for mm=1:M
if mm ~= m
for k=1:K
u2(nr,nt,m,k,mm)=(b(nr))exp(-1ipi(b(nr)cos(ang_estimated(m,k))+a(nt)cos(ang_estimated(mm,k))));
u2_par_m(nr,nt,m,k,mm)=(b(nr))^2exp(-1ipi*(b(nr)*cos(ang_estimated(m,k))+a(nt)*cos(ang_estimated(mm,k))));
u2_par_mprime(nr,nt,m,k,mm)=(b(nr)a(nt))exp(-1ipi(b(nr)*cos(ang_estimated(m,k))+a(nt)*cos(ang_estimated(mm,k))));
end
end
end
end
end
end
lambda1_hat=zeros(Nt,M,K);
lambda1_hat_temp=zeros(Nt,M,K);
lambda2_hat=zeros(Nt,M,K,M);
lambda2_hat_temp=zeros(Nt,M,K,M);
for m=1:M
for k=1:K
for nr=1:Nr
lambda1_hat_temp(:,m,k)=u1(nr,:,m,k)‘+lambda1_hat_temp(:,m,k);
end
lambda1_hat(:,m,k)=(sqrt(2)/sigma_r)*q(m,k)*beta_tilde(m,k,m)*lambda1_hat_temp(:,m,k);
end
for mm=1:M
if mm~=m
for k=1:K
for nr=1:Nr
lambda2_hat_temp(:,m,k,mm)=u2(nr,:,m,k,mm)’+lambda2_hat_temp(:,m,k,mm);
end
lambda2_hat(:,m,k,mm)=(sqrt(2)/sigma_r)*q(m,k)*beta_tilde(m,k,mm)*lambda2_hat_temp(:,m,k,mm);
end
end
end
end

d1=zeros(Nt,M,K);
d1_temp=zeros(Nt,M,K);
d2=zeros(Nt,M,K);
d2_temp=zeros(Nt,M,K);
D=zeros(Nt,M,K);
Sigma2=zeros(Nt,Nt,M,K);
for m=1:M
for k=1:K
for nr=1:Nr
d1_temp(:,m,k)=u1(nr,:,m,k)‘+d1_temp(:,m,k);
d2_temp(:,m,k)=u1_par(nr,:,m,k)’+d2_temp(:,m,k);
end
d1(:,m,k)=(sqrt(2)/sigma_r)(1ipi*cos(ang_estimated(m,k)))*beta_tilde(m,k,m)*d1_temp(:,m,k);
d2(:,m,k)=(sqrt(2)/sigma_r)q(m,k)^2beta_tilde(m,k,m)*10^(-2)*d2_temp(:,m,k);
D(:,m,k)=d1(:,m,k)+d2(:,m,k);
Sigma2(:,:,m,k)=D(:,m,k)*D(:,m,k)'*gamma1;
end
end

e1=zeros(Nt,M,K,M);
e1_temp=zeros(Nt,M,K,M);
e2=zeros(Nt,M,K,M);
e2_temp=zeros(Nt,M,K,M);
E=zeros(Nt,M,K,M);
F=zeros(Nt,M,K,M);
F_temp=zeros(Nt,M,K,M);
Sigma3=zeros(Nt,Nt,M,K,M);
for m=1:M
for k=1:K
for mm=1:M
if mm ~= m
for nr=1:Nr
e1_temp(:,m,k,mm)=u2(nr,:,m,k,mm)‘+e1_temp(:,m,k,mm);
e2_temp(:,m,k,mm)=u2_par_m(nr,:,m,k,mm)’+e2_temp(:,m,k,mm);
F_temp(:,m,k,mm)=u2_par_mprime(nr,:,m,k,mm)'+F_temp(:,m,k,mm);
end
e1(:,m,k,mm)=(sqrt(2)/sigma_r)(1ipicos(ang_estimated(m,k)))beta_tilde(m,k,mm)e1_temp(:,m,k,mm);
e2(:,m,k,mm)=(sqrt(2)/sigma_r)q(m,k)^2beta_tilde(m,k,mm)10^(-2)e2_temp(:,m,k,mm);
E(:,m,k,mm)=e1(:,m,k,mm)+e2(:,m,k,mm);
F(:,m,k,mm)=(sqrt(2)/sigma_r)q(m,k)^2beta_tilde(m,k,mm)10^(1)F_temp(:,m,k,mm);
Sigma3(:,:,m,k,mm)=(E(:,m,k,mm)E(:,m,k,mm)'+F(:,m,k,mm)F(:,m,k,mm)')gamma1;
end
end
end
end
% Distance CRLB
q2=1i2pi2/c;
q3=1i2pi/c;
u3=zeros(L,M,K);
u4=zeros(L,M,K,M);
u3_par=zeros(L,M,K);
u4_par=zeros(L,M,K,M);
f=zeros(L,1);
for l=1:L
f(l)=fc+(l-1)delta_f;
for m=1:M
for k=1:K
u3(l,m,k)=f(l)exp(1i2pif(l)(dis_estimated(m,k)+dis_estimated(m,k))/c);
u3_par(l,m,k)=f(l)^2exp(1i2pif(l)(dis_estimated(m,k)+dis_estimated(m,k))/c);
end
for mm=1:M
if mm~=m
for k=1:K
u4(l,m,k,mm)=f(l)exp(1i2pif(l)(dis_estimated(m,k)+dis_estimated(mm,k))/c);
u4_par(l,m,k,mm)=f(l)^2exp(1i2pif(l)(dis_estimated(m,k)+dis_estimated(mm,k))/c);
end
end
end
end
end

lambda3_hat=zeros(Nt,M,K);
lambda4_hat=zeros(Nt,M,K,M);
sum_u3=zeros(M,K);
sum_u4=zeros(M,K,M);
for m=1:M
for k=1:K
for l=1:L
sum_u3(m,k)=u3(l,m,k)+sum_u3(m,k);
end
lambda3_hat(:,m,k)=(sqrt(2)/sigma_r)q2beta_tilde(m,k,m)*sum_u3(m,k)*eye(Nt,1);
end
for mm=1:M
if mm~=m
for k=1:K
for l=1:L
sum_u4(m,k,mm)=u4(l,m,k,mm)+sum_u4(m,k,mm);
end
lambda4_hat(:,m,k,mm)=(sqrt(2)/sigma_r)q3beta_tilde(m,k,mm)*sum_u4(m,k,mm)*eye(Nt,1);
end
end
end
end
g=zeros(Nt,M,K);
sum_u3_par=zeros(M,K);
sum_u4_par=zeros(M,K,M);
I=zeros(Nt,M,K,M);
j=zeros(Nt,M,K,M);
Sigma4=zeros(Nt,Nt,M,K);
Sigma5=zeros(Nt,Nt,M,K,M);
for m=1:M
for k=1:K
for l=1:L
sum_u3_par(m,k)=u3_par(l,m,k)+sum_u3_par(m,k);
end
g(:,m,k)=(sqrt(2)/sigma_r)q2^2beta_tilde(m,k,m)*sum_u3_par(m,k)*eye(Nt,1);

    Sigma4(:,:,m,k)=(g(:,m,k)*g(:,m,k)')*gamma2;
    for mm=1:M
        if mm ~= m
            for l=1:L
                sum_u4_par(m,k,mm)=u4_par(l,m,k,mm)+sum_u4_par(m,k,mm);
            end
            I(:,m,k,mm)=(sqrt(2)/sigma_r)*q3^2*beta_tilde(m,k,mm)*sum_u4_par(m,k,mm)*eye(Nt,1);
            j(:,m,k,mm)=(sqrt(2)/sigma_r)*q3^2*beta_tilde(m,k,mm)*sum_u4_par(m,k,mm)*eye(Nt,1);
            Sigma5(:,:,m,k,mm)=(I(:,m,k,mm)*I(:,m,k,mm)'+j(:,m,k,mm)*j(:,m,k,mm)')*gamma2;
        end
    end
end

end
%% Proposed Algorithm
% Initial [Rl,Ru]
Rate_low=0.5ones(K,1);
Rate_up=1ones(K,1);

Rate_all_low=0;
Rate_all_up=0;
for k=1:K
for l=1:L
Rate_all_low=Rate_low(k)+Rate_all_low;
Rate_all_up=Rate_up(k)+Rate_all_up;
end
end
% Start iteration
count_ite=0;
%while abs(Rate_all_up-Rate_all_low) >= 10^(-4)
count_ite=count_ite+1;

Rate_mid=(Rate_low+Rate_up)/2;

% Start Solving Problem
cvx_solver mosek %mosek%sedumi;%sdpt3; 

cvx_begin SDP
    variable W_opt(Nt,Nt,M,K) nonnegative symmetric
    variable x1(K,1) 
    variable y1(K,1)
    variable x2(M,K)
    variable y2(M,K)
    variable x3(M,K)
    variable y3(M,K)
    
    Q1=cvx(zeros(Nt,Nt,K));
    u11=cvx(zeros(Nt,K));
    s1=cvx(zeros(K,1));
    Q1_temp1=cvx(zeros(Nt,Nt,M,K));
    Q1_temp2=cvx(zeros(Nt,Nt,M,K));
    vec_Q1=cvx(zeros(Nt^2,K));
    norm_Q1_u1=cvx(zeros(Nt^2+Nt,K));
    
    Q2=cvx(zeros(Nt,Nt,M,K));
    Q2_temp=cvx(zeros(Nt,Nt,M,K));
    u22=cvx(zeros(Nt,M,K));
    u22_temp=cvx(zeros(Nt,M,K));
    s2=cvx(zeros(M,K));
    s2_temp=cvx(zeros(M,K));
    vec_Q2=cvx(zeros(Nt^2,M,K));
    norm_Q2_u2=cvx(zeros(Nt^2+Nt,M,K));

    Q3=cvx(zeros(Nt,Nt,M,K));
    Q3_temp=cvx(zeros(Nt,Nt,M,K));
    u33=cvx(zeros(Nt,M,K));
    u33_temp=cvx(zeros(Nt,M,K));
    s3=cvx(zeros(M,K));
    s3_temp=cvx(zeros(M,K));
    vec_Q3=cvx(zeros(Nt^2,M,K));
    norm_Q3_u3=cvx(zeros(Nt^2+Nt,M,K));

    P_opt=cvx(zeros(M,1));

    for k=1:K
        for m=1:M
            for i =1: k
                if i~=k
                    Q1_temp1(:,:,m,k)=W_opt(:,:,m,i)+Q1_temp1(:,:,m,k);
                end
            end
            Q1_temp2(:,:,m,k)=(1/(2^(Rate_mid(k,1))-1))*W_opt(:,:,m,k)-Q1_temp1(:,:,m,k);
            Q1(:,:,k)=Sigma1(:,:,m,k)^(1/2)*Q1_temp2(:,:,m,k)*Sigma1(:,:,m,k)^(1/2)+Q1(:,:,k);
            Q1(:,:,k)=0.5*(Q1(:,:,k)+Q1(:,:,k)');
            u11(:,k)=Sigma1(:,:,m,k)^(1/2)*Q1_temp2(:,:,m,k)*h_CSI_hat(:,m,k)+u11(:,k);
            s1(k)=h_CSI_hat(:,m,k)'*Q1_temp2(:,:,m,k)*h_CSI_hat(:,m,k)+s1(k);
            
        end
        s1(k)=s1(k)-sigma_c^2;
        vec_Q1(:,k)=reshape(Q1(:,:,k)',1,[]);
        norm_Q1_u1(1:Nt^2,k)=vec_Q1(:,k);
        norm_Q1_u1(Nt^2+1:Nt^2+Nt,k)=sqrt(2)*u11(:,k);

    end
    for m=1:M
        for k=1:K
            for mm=1:M
                if mm~=m
                    Q2_temp(:,:,m,k)=Sigma3(:,:,m,k,mm)^(1/2)*W_opt(:,:,mm,k)*Sigma3(:,:,m,k,mm)^(1/2)+Q2_temp(:,:,m,k);
                    u22_temp(:,m,k)=Sigma3(:,:,m,k,mm)^(1/2)*W_opt(:,:,mm,k)*lambda2_hat(:,m,k,mm)+u22_temp(:,m,k);
                    s2_temp(m,k)=lambda2_hat(:,m,k,mm)'*W_opt(:,:,mm,k)*lambda2_hat(:,m,k,mm)+s2_temp(m,k);

                    Q3_temp(:,:,m,k)=Sigma5(:,:,m,k,mm)^(1/2)*W_opt(:,:,mm,k)*Sigma5(:,:,m,k,mm)^(1/2)+Q3_temp(:,:,m,k);
                    u33_temp(:,m,k)=Sigma5(:,:,m,k,mm)^(1/2)*W_opt(:,:,mm,k)*lambda4_hat(:,m,k,mm)+u33_temp(:,m,k);
                    s3_temp(m,k)=lambda4_hat(:,m,k,mm)'*W_opt(:,:,mm,k)*lambda4_hat(:,m,k,mm)+s3_temp(m,k);
                
                end
            end
            Q2(:,:,m,k)=Sigma2(:,:,m,k)^(1/2)*W_opt(:,:,m,k)*Sigma2(:,:,m,k)^(1/2)+Q2_temp(:,:,m,k);
            Q2(:,:,m,k)=0.5*(Q2(:,:,m,k)+Q2(:,:,m,k)');
            u22(:,m,k)=Sigma2(:,:,m,k)^(1/2)*W_opt(:,:,m,k)*lambda1_hat(:,m,k)+u22_temp(:,m,k);
            s2(m,k)=lambda1_hat(:,m,k)'*W_opt(:,:,m,k)*lambda1_hat(:,m,k)+s2_temp(m,k)-1/gamma1;

            Q3(:,:,m,k)=Sigma4(:,:,m,k)^(1/2)*W_opt(:,:,m,k)*Sigma4(:,:,m,k)^(1/2)+Q3_temp(:,:,m,k);
            Q3(:,:,m,k)=0.5*(Q3(:,:,m,k)+Q3(:,:,m,k)');
            u33(:,m,k)=Sigma4(:,:,m,k)^(1/2)*W_opt(:,:,m,k)*lambda3_hat(:,m,k)+u33_temp(:,m,k);
            s3(m,k)=lambda3_hat(:,m,k)'*W_opt(:,:,m,k)*lambda3_hat(:,m,k)+s3_temp(m,k)-1/gamma2;
            
            vec_Q2(:,m,k)=reshape(Q2(:,:,m,k)',1,[]);
            norm_Q2_u2(1:Nt^2,m,k)=vec_Q2(:,m,k);
            norm_Q2_u2(Nt^2+1:Nt^2+Nt,m,k)=sqrt(2)*u22(:,m,k);

            vec_Q3(:,m,k)=reshape(Q3(:,:,m,k)',1,[]);
            norm_Q3_u3(1:Nt^2,m,k)=vec_Q3(:,m,k);
            norm_Q3_u3(Nt^2+1:Nt^2+Nt,m,k)=sqrt(2)*u33(:,m,k);
        
        end
    end
    for m=1:M
        for k=1:K
            P_opt(m)=real(trace(W_opt(:,:,m,k)))+P_opt(m);
        end
    end
    
    minimize sum(P_opt)
    subject to
        for k=1:K
            % Constraint
            (real(trace(Q1(:,:,k))-sqrt(-2*log(eps1))*x1(k)+log(eps1)*y1(k)+s1(k))) >=0 ;
            (imag(trace(Q1(:,:,k))-sqrt(-2*log(eps1))*x1(k)+log(eps1)*y1(k)+s1(k))) >=0 ;
            (norm(norm_Q1_u1(:,k))-x1(k))<= 0;
            (y1(k)*eye(Nt)+Q1(:,:,k)) >= 0 ;
            (y1(k)) >=0 ;
        end
        for m=1:M
            for k=1:K
                
                real(trace(Q2(:,:,m,k))-sqrt(-2*log(eps2))*x2(m,k)+log(eps2)*y2(m,k)+s2(m,k)) >=0 ;
                imag(trace(Q2(:,:,m,k))-sqrt(-2*log(eps2))*x2(m,k)+log(eps2)*y2(m,k)+s2(m,k)) >=0 ;
                (norm(norm_Q2_u2(:,m,k)) - x2(m,k))<=0;
                (y2(m,k)*eye(Nt)+Q2(:,:,m,k)) >= 0 ;
                (y2(m,k)) >=0 ;
                
                
                (real(trace(Q3(:,:,m,k))-sqrt(-2*log(eps2))*x3(m,k)+log(eps2)*y3(m,k)+s3(m,k))) >=0 ;
                (imag(trace(Q3(:,:,m,k))-sqrt(-2*log(eps2))*x3(m,k)+log(eps2)*y3(m,k)+s3(m,k))) >=0 ;
                (norm(norm_Q3_u3(:,m,k)) - x3(m,k) )<=0;
                (y3(m,k)*eye(Nt)+Q3(:,:,m,k)) >= 0 ;
                (y3(m,k)) >=0 ;
            end
        end
        
           
cvx_end
   
temp_P=zeros(M,1);
Power_check=zeros(M,1);
for m=1:M
    for k=1:K
        temp_P(m)=trace(W_opt(:,:,m,k))+temp_P(m);
    end
    if temp_P(m)<=P
        Power_check(m)=1;
    else
        Power_check(m)=0;
    end
end

disp('iteration')
disp(count_ite)

% Check Feasibility
%if isnan(mean(temp_P)) == 1
if strfind(cvx_status,'Infeasible') == 1
    disp('Not Feasible')
    Rate_up=Rate_mid;
else
    if sum(Power_check) == M
        disp('Feasible')
        Rate_low=Rate_mid;
    else
        disp('Over Power')
        Rate_up=Rate_mid;
    end
end

Rate_all_low=0;
Rate_all_up=0;
for k=1:K
    for l=1:L
        Rate_all_low=Rate_low(k)+Rate_all_low;
        Rate_all_up=Rate_up(k)+Rate_all_up;
    end
end

%end

%% The value that I’ve tried to scale.
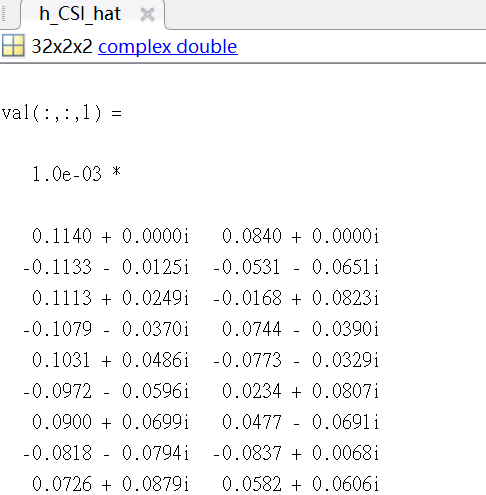
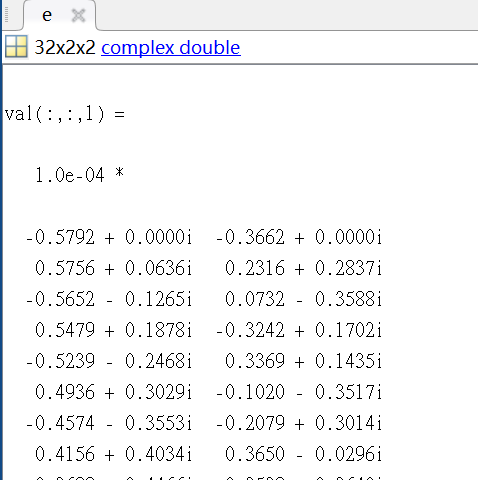
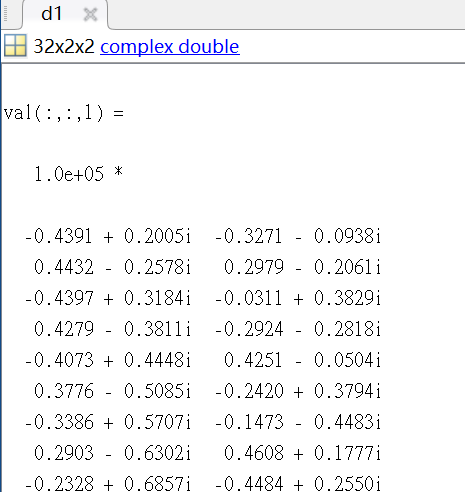
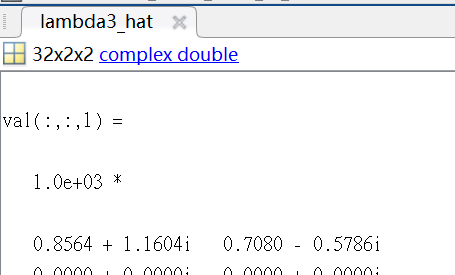
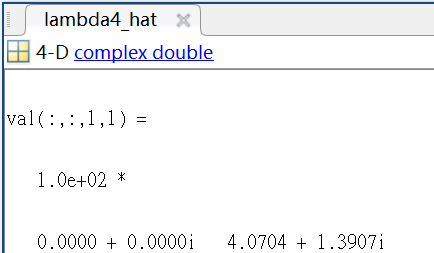
image
image
image

image
image520×525 10.4 KB

image
image451×521 9.11 KB

image
image
image
image464×501 8.67 KB

image
image446×525 8.92 KB

image
image424×537 8.76 KB

image
image
image
image
image

%% Result of Mosek

Problem
Name :
Objective sense : min
Type : CONIC (conic optimization problem)
Constraints : 2136
Cones : 8
Scalar variables : 7478
Matrix variables : 8
Integer variables : 0

Optimizer started.
Presolve started.
Linear dependency checker started.
Linear dependency checker terminated.
Eliminator started.
Freed constraints in eliminator : 0
Eliminator terminated.
Eliminator - tries : 1 time : 0.00
Lin. dep. - tries : 1 time : 0.05
Lin. dep. - number : 0
Presolve terminated. Time: 0.53
Problem
Name :
Objective sense : min
Type : CONIC (conic optimization problem)
Constraints : 2136
Cones : 8
Scalar variables : 7478
Matrix variables : 8
Integer variables : 0

Optimizer - threads : 6
Optimizer - solved problem : the primal
Optimizer - Constraints : 2120
Optimizer - Cones : 8
Optimizer - Scalar variables : 7338 conic : 7326
Optimizer - Semi-definite variables: 8 scalarized : 10432
Factor - setup time : 5.17 dense det. time : 0.00
Factor - ML order time : 0.05 GP order time : 0.00
Factor - nonzeros before factor : 1.12e+06 after factor : 1.12e+06
Factor - dense dim. : 0 flops : 1.81e+10
ITE PFEAS DFEAS GFEAS PRSTATUS POBJ DOBJ MU TIME
0 3.1e+01 4.2e+01 3.3e+02 0.00e+00 -3.268311861e+02 0.000000000e+00 1.0e+00 7.16
1 3.6e+00 4.8e+00 1.5e+02 -1.09e+00 -5.403129854e+02 2.050729865e-05 1.1e-01 26.70
2 1.0e+00 1.4e+00 4.3e+02 -2.24e+00 -4.605145602e+03 -5.359697693e-04 3.3e-02 37.11
3 7.7e-01 1.0e+00 3.9e+02 -4.58e+00 -4.098926852e+03 -1.056707955e-03 2.5e-02 47.34
4 4.4e-01 5.8e-01 1.1e+02 -4.55e-01 -1.411272432e+03 -1.704420428e-03 1.4e-02 57.25
5 2.0e-02 2.7e-02 2.4e+00 8.59e-02 -1.841092167e+02 -3.792939041e-03 6.6e-04 67.75
6 1.4e-04 1.8e-04 1.4e-03 9.73e-01 -1.433663368e+00 -3.919572273e-03 4.5e-06 78.25
7 7.0e-05 9.4e-05 5.2e-04 1.01e+00 -7.229605701e-01 -3.993044100e-03 2.3e-06 88.81
8 4.8e-05 6.5e-05 3.1e-04 9.99e-01 -5.464629915e-01 -3.719505854e-03 1.9e-06 99.16
9 2.3e-05 3.1e-05 1.1e-04 5.94e-01 -3.147652787e-01 -4.004794893e-03 9.3e-07 109.50
10 1.8e-05 2.4e-05 7.9e-05 6.59e-01 -2.588036412e-01 -4.207884687e-03 7.4e-07 119.78
11 1.4e-05 1.8e-05 4.9e-05 7.97e-01 -1.797161444e-01 -4.043708261e-03 5.9e-07 130.28
12 7.5e-06 1.0e-05 2.3e-05 3.87e-01 -1.290227220e-01 -4.628552345e-03 3.3e-07 141.16
13 6.9e-06 9.2e-06 2.0e-05 3.60e-01 -1.211408340e-01 -4.684624968e-03 3.1e-07 152.45
14 4.5e-06 6.0e-06 1.2e-05 6.09e-01 -9.055986237e-02 -4.933807470e-03 2.2e-07 163.09
15 3.8e-06 5.1e-06 8.8e-06 6.62e-01 -7.539312618e-02 -4.866138767e-03 1.9e-07 174.55
16 2.4e-06 3.3e-06 5.5e-06 2.39e-01 -6.952780650e-02 -5.744920705e-03 1.3e-07 186.45
17 1.7e-06 2.3e-06 3.4e-06 3.74e-01 -5.357948920e-02 -5.833588259e-03 9.0e-08 197.75
18 1.7e-06 2.3e-06 3.4e-06 1.57e+00 -5.357948920e-02 -5.833588259e-03 9.0e-08 208.30
19 1.7e-06 2.3e-06 3.4e-06 4.14e+00 -5.357948920e-02 -5.833588259e-03 9.0e-08 219.38
Optimizer terminated. Time: 230.36

Interior-point solution summary
Problem status : ILL_POSED
Solution status : PRIMAL_ILLPOSED_CER
Dual. obj: -8.0365732125e-06 nrm: 1e+02 Viol. con: 0e+00 var: 6e-02 barvar: 3e-08 cones: 0e+00
Optimizer summary
Optimizer - time: 230.36
Interior-point - iterations : 20 time: 230.33
Basis identification - time: 0.00
Primal - iterations : 0 time: 0.00
Dual - iterations : 0 time: 0.00
Clean primal - iterations : 0 time: 0.00
Clean dual - iterations : 0 time: 0.00
Simplex - time: 0.00
Primal simplex - iterations : 0 time: 0.00
Dual simplex - iterations : 0 time: 0.00
Mixed integer - relaxations: 0 time: 0.00

Status: Failed
Optimal value (cvx_optval): NaN

Thanks for the help !

2

You’re right, the scaling is terrible. That might make any solver outcome unreliable. So the first thing to do is improve scaling. The rescaling should be done in such a way that if the rescaled problem were solved exactly (in infinite precision), it should be mathematically equivalent to the original problem. But because the solvers work in double precision, the original and rescaled problems are not numerically equivalent when actually solved; and the solver might have a different outcome on the rescaled problem than on the original problem.

Mosek does not conclude the problem is infeasible. It reports primal ill-posed. Because you didn’t show the portion of CVX output prior to Mosek output, the forum readers don’t know whether Mosek was provided the dual by CVX, in which case Mosek’s conclusion of primal ill-posed would correspond to the original problem being dual ill-posed.

3

Hi, Mark. Thanks for your reply !
But sorry I don’t understand what CVX output means. The window only shows the mosek output :

Calling Mosek 9.1.9: 19263 variables, 2142 equality constraints
For improved efficiency, Mosek is solving the dual problem.

MOSEK Version 9.1.9 (Build date: 2019-11-21 11:34:40)
Copyright (c) MOSEK ApS, Denmark. WWW: mosek.com
Platform: Windows/64-X86

MOSEK warning 960: E[30,30] = 1.0e+10 is large in absolute size.
MOSEK warning 960: E[31,30] = -1.0e+10 is large in absolute size.
MOSEK warning 960: E[31,31] = 1.1e+10 is large in absolute size.
MOSEK warning 960: E[62,62] = 1.0e+10 is large in absolute size.
MOSEK warning 960: E[63,62] = -1.0e+10 is large in absolute size.
MOSEK warning 960: E[63,63] = 1.1e+10 is large in absolute size.
MOSEK warning 960: E[27,27] = -1.0e+10 is large in absolute size.
MOSEK warning 960: E[28,27] = 1.1e+10 is large in absolute size.
MOSEK warning 960: E[28,28] = -1.1e+10 is large in absolute size.
MOSEK warning 960: E[29,27] = -1.1e+10 is large in absolute size.
Warning number 960 is disabled.
MOSEK warning 710: #384 (nearly) zero elements are specified in sparse col ‘’ (1) of matrix ‘A’.
MOSEK warning 710: #366 (nearly) zero elements are specified in sparse col ‘’ (5) of matrix ‘A’.
MOSEK warning 710: #552 (nearly) zero elements are specified in sparse col ‘’ (32) of matrix ‘A’.
MOSEK warning 710: #523 (nearly) zero elements are specified in sparse col ‘’ (33) of matrix ‘A’.
MOSEK warning 710: #985 (nearly) zero elements are specified in sparse col ‘’ (34) of matrix ‘A’.
MOSEK warning 710: #618 (nearly) zero elements are specified in sparse col ‘’ (35) of matrix ‘A’.
MOSEK warning 710: #937 (nearly) zero elements are specified in sparse col ‘’ (36) of matrix ‘A’.
MOSEK warning 710: #458 (nearly) zero elements are specified in sparse col ‘’ (37) of matrix ‘A’.
MOSEK warning 710: #979 (nearly) zero elements are specified in sparse col ‘’ (38) of matrix ‘A’.
MOSEK warning 710: #452 (nearly) zero elements are specified in sparse col ‘’ (39) of matrix ‘A’.
Warning number 710 is disabled.
MOSEK warning 62: The A matrix contains a large value of -1.0e+10 in constraint ‘’ (1045) at variable ‘’ (4647).
MOSEK warning 62: The A matrix contains a large value of 1.0e+10 in constraint ‘’ (1049) at variable ‘’ (4647).
MOSEK warning 62: The A matrix contains a large value of 1.0e+10 in constraint ‘’ (1045) at variable ‘’ (4695).
MOSEK warning 62: The A matrix contains a large value of -1.0e+10 in constraint ‘’ (1049) at variable ‘’ (4695).
MOSEK warning 62: The A matrix contains a large value of -1.0e+10 in constraint ‘’ (1018) at variable ‘’ (4703).
MOSEK warning 62: The A matrix contains a large value of -1.1e+10 in constraint ‘’ (1027) at variable ‘’ (4703).
MOSEK warning 62: The A matrix contains a large value of -1.1e+10 in constraint ‘’ (1039) at variable ‘’ (4703).
MOSEK warning 62: The A matrix contains a large value of 1.1e+10 in constraint ‘’ (1044) at variable ‘’ (4703).
MOSEK warning 62: The A matrix contains a large value of -1.1e+10 in constraint ‘’ (1045) at variable ‘’ (4703).
MOSEK warning 62: The A matrix contains a large value of 1.1e+10 in constraint ‘’ (1049) at variable ‘’ (4703).
Warning number 62 is disabled.
Problem
Name :
Objective sense : min
Type : CONIC (conic optimization problem)
Constraints : 2142
Cones : 10
Scalar variables : 11007
Matrix variables : 10
Integer variables : 0

Optimizer started.
Presolve started.
Linear dependency checker started.
Linear dependency checker terminated.
Eliminator started.
Freed constraints in eliminator : 0
Eliminator terminated.
Eliminator - tries : 1 time : 0.00
Lin. dep. - tries : 1 time : 0.03
Lin. dep. - number : 0
Presolve terminated. Time: 0.63
Problem
Name :
Objective sense : min
Type : CONIC (conic optimization problem)
Constraints : 2142
Cones : 10
Scalar variables : 11007
Matrix variables : 10
Integer variables : 0

Optimizer - threads : 6
Optimizer - solved problem : the primal
Optimizer - Constraints : 2122
Optimizer - Cones : 10
Optimizer - Scalar variables : 10861 conic : 10847
Optimizer - Semi-definite variables: 10 scalarized : 14592
Factor - setup time : 1.38 dense det. time : 0.00
Factor - ML order time : 0.08 GP order time : 0.00
Factor - nonzeros before factor : 2.24e+06 after factor : 2.24e+06
Factor - dense dim. : 0 flops : 2.58e+10
ITE PFEAS DFEAS GFEAS PRSTATUS POBJ DOBJ MU TIME
0 3.1e+01 4.2e+01 3.3e+02 0.00e+00 -3.268311887e+02 0.000000000e+00 1.0e+00 3.81
1 4.2e+00 5.6e+00 1.4e+02 -1.09e+00 -4.607130787e+02 1.269031247e-05 1.3e-01 21.66
2 1.0e+00 1.3e+00 3.4e+02 -1.83e+00 -3.256825579e+03 -4.238092472e-04 3.2e-02 30.77
3 5.9e-01 7.9e-01 2.6e+02 -3.72e+00 -2.933831368e+03 -1.343701919e-03 1.9e-02 40.05
4 8.0e-02 1.1e-01 1.1e+01 1.24e-01 -3.980926727e+02 -3.290123102e-03 2.6e-03 49.19
5 2.5e-04 3.3e-04 3.4e-03 7.91e-01 -2.526831917e+00 -3.921934113e-03 8.1e-06 58.78
6 7.5e-05 1.0e-04 5.8e-04 9.77e-01 -8.052143197e-01 -4.023134213e-03 2.5e-06 67.73
7 5.7e-05 7.6e-05 3.8e-04 9.18e-01 -6.141491695e-01 -3.955629340e-03 1.8e-06 76.70
8 4.9e-05 6.6e-05 3.3e-04 4.76e-01 -6.036281390e-01 -4.120693529e-03 1.6e-06 85.70
9 2.3e-05 3.0e-05 1.4e-04 5.15e-01 -4.823753551e-01 -5.086454139e-03 7.8e-07 94.42
10 1.8e-05 2.4e-05 1.1e-04 4.83e-01 -4.345885607e-01 -5.502213824e-03 6.4e-07 103.16
11 1.1e-05 1.4e-05 4.4e-05 6.14e-01 -2.189289429e-01 -5.414608456e-03 3.9e-07 112.08
12 7.9e-06 1.1e-05 2.9e-05 6.52e-01 -1.820349028e-01 -5.885465208e-03 3.2e-07 120.80
13 5.8e-06 7.7e-06 2.2e-05 3.59e-01 -1.873834532e-01 -7.382172878e-03 2.7e-07 129.66
14 4.8e-06 6.3e-06 1.7e-05 3.02e-01 -1.731892967e-01 -7.930201335e-03 2.5e-07 138.34
15 2.5e-06 3.3e-06 1.1e-05 -5.03e-01 -2.460547660e-01 -1.281044814e-02 1.4e-07 148.30
16 2.5e-06 3.3e-06 1.1e-05 -1.42e-01 -2.460547660e-01 -1.281044814e-02 1.4e-07 157.36
17 2.5e-06 3.3e-06 1.1e-05 8.58e-01 -2.460547660e-01 -1.281044814e-02 1.4e-07 166.55
Optimizer terminated. Time: 176.06

Interior-point solution summary
Problem status : ILL_POSED
Solution status : PRIMAL_ILLPOSED_CER
Dual. obj: -8.7695701287e-06 nrm: 3e+02 Viol. con: 0e+00 var: 3e-02 barvar: 8e-08 cones: 0e+00
Optimizer summary
Optimizer - time: 176.06
Interior-point - iterations : 18 time: 176.05
Basis identification - time: 0.00
Primal - iterations : 0 time: 0.00
Dual - iterations : 0 time: 0.00
Clean primal - iterations : 0 time: 0.00
Clean dual - iterations : 0 time: 0.00
Simplex - time: 0.00
Primal simplex - iterations : 0 time: 0.00
Dual simplex - iterations : 0 time: 0.00
Mixed integer - relaxations: 0 time: 0.00

Status: Failed
Optimal value (cvx_optval): NaN

4

Also, about the rescaling problem.
Do you mean that the solver only works in double precision, so that the rescaled problem might be different with the orginal problem ?
If true, rescaling the problem changes my original problem, and is this changing the optimization performance of my original problem ?
Thanks again for the reply !

5

Mosek warned about both very large magnitude numbers, and very small magnitude non-zero numbers. You should try to rescale so that Mosek does not issue any warnings. And preferably, rescale as well as you can, better than just enough to eliminate the warning messages.

The bold output prior to Mosek output is from CVX, not Mosek. It shows that Mosek was provided the dual. Therefore Mosek’s assessment should be interpreted that the dual problem is ill-posed (at least as it appeared to Mosek with the horrible scaling).

In your first post, you also cut off the beginning of the Mosek output, consisting of its warnings. I could look at your inputs and guess there would be such warnings.

As for scaling, you could formulate a problem in kilometers or nanometers (which differ by a factor of 1e13), in such a way that the model stayed mathematically equivalent in exact arithmetic. But one of these might be much better than the other for Mosek, which like other solvers called by CVX, operates in double precision. For example, if a distance is constrained to 10 km, then you should use 10 (km), instead of 1e13 nm. If a distance is constrained to 0.1 nm, you should used 0.1 (nm) rather than 1e-13 km.

6

Hi Mark, thanks for the reply !
I’ve beriefly understood what you have said, your explaination is perfect !
However, I have used a bisection iterative method to solve the problem, It seems to be not possible to rescale the value manually every iteration.
Is there any suggestion that I can do ? Thanks again !

7

Sorry, I’ve got one more question.
Is manually rescaling the constraint a good way to solve the infeasible solution ? I’ve tried rescaling as the code below and it works ! But I’m wondering if it’s a good way to solve it. Thanks again !

   minimize sum(P_opt)
    subject to
        for k=1:K
            % Constraint
            10^(20)*(real(trace(Q1(:,:,k))-sqrt(-2*log(eps1))*x1(k)+log(eps1)*y1(k)+s1(k))) >=0 ;
            10^(22)*(imag(trace(Q1(:,:,k))-sqrt(-2*log(eps1))*x1(k)+log(eps1)*y1(k)+s1(k))) >=0 ;
            10^(9)*(norm(norm_Q1_u1(:,k))-x1(k))<= 0;
            10^(9)*(y1(k)*eye(Nt)+Q1(:,:,k)) >= 0 ;
            10^(10)*(y1(k)) >=0 ;
        end
        for m=1:M
            for k=1:K
                
                10^2*real(trace(Q2(:,:,m,k))-sqrt(-2*log(eps2))*x2(m,k)+log(eps2)*y2(m,k)+s2(m,k)) >=0 ;
                imag(trace(Q2(:,:,m,k))-sqrt(-2*log(eps2))*x2(m,k)+log(eps2)*y2(m,k)+s2(m,k)) >=0 ;
                10^(-12)*(norm(norm_Q2_u2(:,m,k)) - x2(m,k))<=0;
                10^(-8)*(y2(m,k)*eye(Nt)+Q2(:,:,m,k)) >= 0 ;
                (y2(m,k)) >=0 ;
                
                
                10^(10)*(real(trace(Q3(:,:,m,k))-sqrt(-2*log(eps2))*x3(m,k)+log(eps2)*y3(m,k)+s3(m,k))) >=0 ;
                (imag(trace(Q3(:,:,m,k))-sqrt(-2*log(eps2))*x3(m,k)+log(eps2)*y3(m,k)+s3(m,k))) >=0 ;
                10^(-5)*(norm(norm_Q3_u3(:,m,k)) - x3(m,k) )<=0;
                10^(-5)*(y3(m,k)*eye(Nt)+Q3(:,:,m,k)) >= 0 ;
                10^(-5)*(y3(m,k)) >=0 ;
            end
        end
8

In general, multiplying a whole constraint by a very large or very small number iis a bad thing to do. You don’t want big or small numbers to ever be processed by CVX. If big*small is input data and is within parentheses, it might be o.k. But if not “netted out” by MATLAB prior to being read in by CVX, it could be very bad.

As for the bisection, if it is inherently badly scaled, or the scaling changes on every subproblem, I’m not sure what you should do. Your problem is sufficiently complicated that I can’t just look at it and know immediately what to do. Perhaps your overall model needs to be improved, or a different solution method used.

9

Hi, Mark.
Thanks for your reply !
I’ve tried rescaling my problem and it works !
Thanks again for your help !