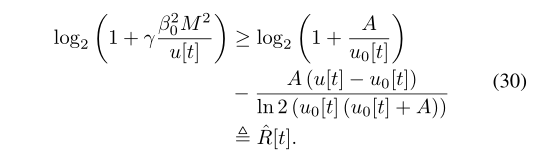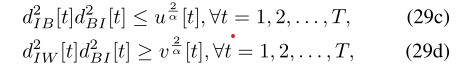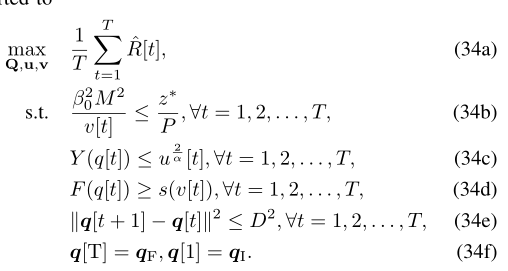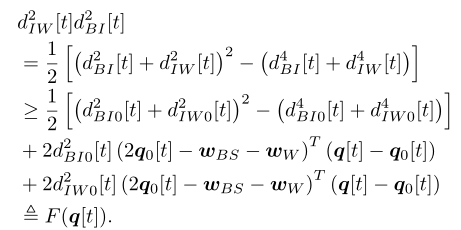求助，为什么我这个cvx解不出来，使用的是sca

1

clc
clear
o=0;
M=30;
xBS= 0;
yBS = 0;

xBob= 0;
yBob = 100;

xW= 0;
yW = 150;

x0=-200;
y0=0;
xF=200;
yF=0;
H=50;
P=1000;
rouw=6;
Vmax=50;
sigmaK=db2pow(-120);

Nx = 5; % IRS单元个数
Ny = 6;
N = NxNy;
beta0=db2pow(-50);
alphaIB = 2.2;
alphaBI = 2.2;
beta_BI = db2pow(3); % AP到RIS之间考虑莱斯信道，莱斯因子为3dB
beta_IB = db2pow(3); % IRS到User考虑瑞利莱斯信道，莱斯因子为3dB
theta = 2pirand(1,N); % 随机初始化IRS的相位
Theta = diag(exp(1itheta));

theta_BI=zeros(M,1);
theta_IB=zeros(M,1);
x_fea2=zeros(M,1);
y_fea2=zeros(M,1);
u0=zeros(M,1);
v0=zeros(M,1);
dBI0=zeros(M,1);
dIB0=zeros(M,1);
dIW0=zeros(M,1);
s0=zeros(M,1);
t0=zeros(M,1);
k0=zeros(M,1);
l0=zeros(M,1);
for i=1:M
x_fea2(i)=-200+(40/3)i;
y_fea2(i)=-abs(x_fea2(i))+200;
u0(i)=((x_fea2(i)^2+y_fea2(i)^2+H^2)^1.1)((x_fea2(i)^2+(y_fea2(i)-yBob)^2+H^2)^1.1);
v0(i)=((x_fea2(i)^2+y_fea2(i)^2+H^2)^1.1)*((x_fea2(i)^2+(y_fea2(i)-yW)^2+H^2)^1.1);
dBI0(i)=sqrt((x_fea2(i)^2+y_fea2(i)^2+H^2));
dIB0(i)=sqrt((x_fea2(i)^2+(y_fea2(i)-yBob)^2+H^2));
dIW0(i)=sqrt((x_fea2(i)^2+(y_fea2(i)-yW)^2+H^2));

end

eps = 1e-3;
maxIter = 20;

r0=0;
r=0;
hBI=zeros(M,N);
hIB=zeros(M,N);
count = 0;
K_AI = db2pow(10);

z2 = zeros(M,1);
Rate = zeros(M,1);

a=zeros(1,M);
A=Pbeta0^2N^2/sigmaK;

for i=1:M
a(i)=A/(log(2)u0(i)(u0(i)+A));
end

t2=-au0;
z1=sigmaK(exp(0.012log(rouw))-1)/(rouwP);
d0=zeros(M,1);
d1=zeros(M,1);
for i=1:M
d0(i)=0.5((dBI0(i)+dIB0(i))^2-(dBI0(i)^2+dIB0(i)^2));
d1(i)=0.5*((dBI0(i)+dIW0(i))^2-(dBI0(i)^2+dIW0(i)^2));
end

for i=1:M
dBI(i)=sqrt((x_fea2(i)-xBS)^2+(y_fea2(i)-yBS)^2+H^2);
dIB(i)=sqrt((x_fea2(i)-xBob)^2+(y_fea2(i)-yBob)^2+H^2);
theta_BI(i) = (x_fea2(i)-xBS)/dBI(i);
theta_IB(i) = (x_fea2(i)-xBob)/dIB(i);
hBI(i,:)=sqrt(beta0dBI(i)^(-alphaBI))(sqrt(beta_BI/(1+beta_BI))URA_sv(theta_BI(i),0,Nx,Ny)+sqrt(1/(1+beta_BI))(randn(N,1)+1irandn(N,1)/sqrt(2)));
hIB(i,:)=sqrt(beta0dBI(i)^(-alphaIB))(sqrt(beta_IB/(1+beta_IB))URA_sv(theta_IB(i),0,Nx,Ny)+sqrt(1/(1+beta_IB))(randn(N,1)+1irandn(N,1)/sqrt(2)));
thetaBI(i,:)=angle(hBI(i,:));
thetaIB(i,:)=angle(hIB(i,:));
end

cvx_begin
variable x(M,1)
variable y(M,1)
variable u(M,1)
variable v(M,1)
expression t1
t1=-au/M;
maximize t1
subject to
for i=1:M
N^2beta0^2<=z1*v(i);
end

for i=1:M-1
(x(i+1)-x(i))^2+(y(i+1)-y(i))^2<=Vmax^2;
end
x(1)==x0;
y(1)==y0;
x(M)==xF;
y(M)==yF;

for i=1:M
u(i)^(1/2.2)>=d0(i)-(2x_fea2(i)(x(i)-x_fea2(i))+(2y_fea2(i)-yBob)(y(i)-y_fea2(i)));
d1(i)+(dBI0(i)+dIW0(i))((x_fea2(i)(x(i)-x_fea2(i))+y_fea2(i)(y(i)-y_fea2(i)))/dBI0(i)+(x_fea2(i)(x(i)-x_fea2(i))+(y_fea2(i)-yW)(y(i)-y_fea2(i)))/dIW0(i))>=v0(i)^(1/2.2)+v0(i)^((1/2.2)-1)(v(i)-v0(i))/2.2;
end
cvx_end

2

Do you have a que4stion or difficulty? Please tell us.

4

mmexport1685606543201
mmexport1685606543201
mmexport1685606547219

5

mmexport1685606541111

6

I think it’s because there’s a problem with the constraints of 29c and 29d, but I don’t know how to change it, where d is the distance

7

Unless \alpha = 2, I don’t see how both 29c and 29d could be convex constraints.

8

I conducted Taylor expansion on 29c and 29d

9

mmexport1685622530597
mmexport1685622524070

10

d0=zeros(M,1);
d1=zeros(M,1);
for i=1:M
d0(i)=0.5*((dBI0(i)^2+dIB0(i)^2)^2-(dBI0(i)^4+dIB0(i)^4));
d1(i)=0.5*((dBI0(i)^2+dIW0(i)^2)^2-(dBI0(i)^4+dIW0(i)^4));
end

d0(i)-2dBI0(i)^2(x_fea2(i)(x(i)-x_fea2(i))+y_fea2(i)(y(i)-y_fea2(i)))-2dIB0(i)^2(x_fea2(i)(x(i)-x_fea2(i))+(y_fea2(i)-yBob)(y(i)-y_fea2(i)))<=u(i)^(2/2.2);
d1(i)+(2dBI0(i)^2+2dIW0(i)^2)(2x_fea2(i)(x(i)-x_fea2(i))+(2y_fea2(i)-yW)(y(i)-y_fea2(i)))>=real(v0(i)^(2/2.2)+2v0(i)^((2/2.2)-1)*(v(i)-v0(i))/2.2);

11

If you still have a difficulty, please tell us what it is. We are not mind readers.

If the difficulty is that you are using SCA and it fails, the following may apply:

Unsafeguarded (no line search or trust region) SCA is unreliable. It might not descend (for minimization problem), i.e., iterates could get worse. It might not converge to anything; and if it does converge, it might not be to a local optimum of the original problem, let alone a global optimum. The solution of successive iterations, and therefore subproblem inputs, can become wilder and wilder, until at some point the solver fails, or makes erroneous determination of infeasibility or unboundedness.

https://twitter.com/themarklstone/status/1586795881168265216

1 Like
12

cvx solution is -inf,i don’t know how can i deal with

13

i think maybe my sca was wrong? but what is true

14

If you are maximizing and cvx_optval is -inf, that means the problem is infeasible, which should be reported by CVX Status. Your crude implementation of SCA provides no guarantee that the optimization problems it generates and attempts to solve will be feasible, even if the original non-convex problem is feasible. If you try a different starting point (initial value), you might get lucky.