Cvx optimization Problem

1

Hello, I’m new to cvx and optimization in general and I’m trying to find the optimal sensor location of a set of sensors by maximizing the minimum eigenvalue of a gram matrix.
sssw

Unbenannt
Where W_o ist the sum of the gramians for each sensor position 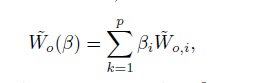sss

I’d tried to solve the problem like this:

n=size(A,1);
C=zeros(n,n);
m=10;
sumGramian=0;

cvx_begin
variable b(m)
for i=1:n
C(i,i)=1;
gramian(:,:,i)=lyap(A’,C’*C);
C(i,i)=0;
sumGramian=sumGramian+gramian(:,:,i)*b;
end

maximize(lambda_min(sumGramian))

subject to
b >= 0;
b <= 1;
sum(b)<=4;
cvx_end

where A is 10x10 matrix created with matlabs rss() function. My problem is that I don’t get a matrix to maximize, because the gramian matrix is multiplied by a vector. If i change the activation b function to a nxn matrix my solution looks like this:

b:
(1,1) 0.4000
(2,2) 0.4000
(3,3) 0.4000
(4,4) 0.4000
(5,5) 0.4000
(6,6) 0.4000
(7,7) 0.4000
(8,8) 0.4000
(9,9) 0.4000
(10,10) 0.4000

But I’d like to use only a specific amount of sensors to maximize the function and not all sensors. Can anybody help me pls?

The optimization problem is from this paper: https://ieeexplore.ieee.org/document/9483072

2

In the CVX forum, the question asker is assumed to have determined the convex optimization problem they wish to solve with CVX. This is not the right place to figure out how to model an optimal sensor location problem as a convex optimization problem. There is a huge literature on such things, some of which explicitly make use of CVX.

3

The problem is already formualted as a convex optimization problem and I’m trying to implement it to cvx. I did get the desired result for maximizing the trace setting the activation function as a matrix, but it doesn’t work for maximizing the minimum eigenvalue.

4

The matter of what constitutes a good convex optimization problem formulation for your purpose is what is your responsibility. This forum does not specialize in producing good formulations for the real world problem of interest.

You should look at problem inputs to make sure they are not too extreme (large or small) in magnitude, and look at solver output. Perhaps the Gramian is very ill-conditioned, which is causing difficulties or inaccuracies for the solver.

5

Sorry, but I don’t get the issue with my question.

I’m trying to implement the optimization problem:Unbenannt

Where c is the amount of sensors I want to use in my case 4 and p is the total number of sensors.
My objective function is like this sssw.
I’d try to solve the problem like in the code I posted, but it didn’t work and I tried to solve it by setting the activiation function beta as a matrix and I did get the result I posted in the first post. Like I said for maximizing the trace I did get the desired solution. Can you tell me what I’m doing wrong?

6

gramian(:,:,i)*b(i) not gramian(:,:,i)*b

7

Thank you, I came to the same conclusion, but than I get the following solution:

b =

0.5227
     0
     0
     0
     0
     0
     0
     0
     0
     0
8

Perhaps it’s optimal to put everything it has on the first Gramian, because mixing (adding) in some other Gramians only serves to decrease the minimum eigenvalue.I’m not the domain expert, so I have no idea what solutions make sense.

9

Ok, thank you I got it know.
I forgot to change the variable into a vector, thats why I just got one value.
Now I do get the following solution:

0.3925
0.4173
0.2421
0.4455
0.7078
0.7648
0.2064
0.6077
0.6004
0.6154

I guess, the rows with the highest values represent the best sensor locations, right?

10

I don’t know. It’s your problem, not mine.