Hi, everyone
I encounter problem using CVX, specifically, matlab codes are given as following:
function [ Belta1_out,Belta2_out] = CvxFixedPower( Snr_PS,Snr_PR )
%UNTITLED3 此处显示有关此函数的摘要
% 此处显示详细说明
global N m x0 y0 xF yF T_slot G H;
cvx_begin
variable x(N)
variable y(N)
expression Belta1(N-1)
expression Belta2(N-1)
expression SumBelta1(N-1)
expression SumBelta2(N-1)
for i=1:N-1
Belta1(i)= G*inv_pos(power((power(x(i),2)+power(y(i),2)+H^2),m/2));
end
for i=1:N-1
Belta2(i)= G*inv_pos(power((power(x(i)-D,2)+power(y(i),2)+H^2),m/2));
end
% Belta1= G*inv_pos(power((power(x(1:N-1),2)+power(y(N-1),2)+H^2),m/2));
% Belta2= G*inv_pos(power((power(x(1:N-1)-D,2)+power(y(N-1),2)+H^2),m/2));
for i=1:N-1
SumBelta1(i)=inv_pos(Belta1(i)*Snr_PS(i));
end
for i=1:N-1
SumBelta2(i)=inv_pos(Belta2(i)*Snr_PR(i));
end
minimize sum(SumBelta1+SumBelta2)
subject to
power(x(1)-x0,2)+power(y(1)-y0,2)-(T_slot*V_Max)^2<=0;
for k=1:N-1
power(x(k+1)-x(k),2)+power(y(k+1)-y(k),2)-(T_slot*V_Max)^2<=0;
end
power(x(N)-xF,2)+power(y(N)-yF,2)-(T_slot*V_Max)^2<=0;
cvx_end
Belta1_out=G./(power(x(1:N-1),2)+power(y(1:N-1),2)+H^2).^(m/2);
Belta2_out=G./(power(x(1:N-1)-D,2)+power(y(1:N-1),2)+H^2).^(m/2);
end
However, Matlab gives messages error using
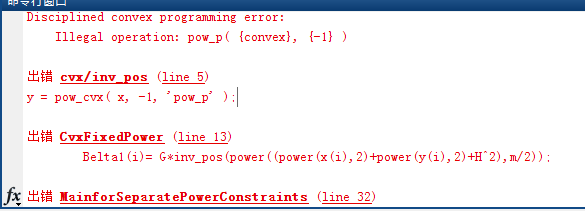
Actually, the formula in line 13 is given as following
[\beta {\rm{ = }}\frac{G}{{{{\left( {{x^2}[n] + {y^2}[n] + {H^2}} \right)}^{{m \mathord{\left/
{\vphantom {m 2}} \right.
\kern-\nulldelimiterspace} 2}}}}}]
Thanks anyone who can help me.