CVX for minimizing abs of norm

Nonconvex
1

Hi,
I’m trying to solve the following problem
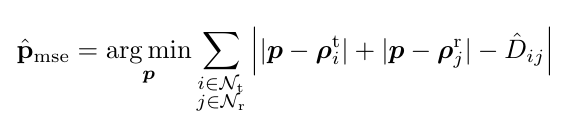
image
where \{\hat{D}_{ij}\}, \{\boldsymbol{\rho}^{\rm t}_i\}, and \{\boldsymbol{\rho}^{\rm r}_j\} are known. Here are the code:

cvx_begin quiet
variable x(2,1);
expression obj;
obj = 0;
for i=1:length(Txlist)
for j=1:length(Rxlist)
if bistatic_distance(i,j) <= distance_threshold
dist_sum = norm(x’ - Txlist(i).location,2) + norm(x’ - Rxlist(j).location,2);
obj = obj + abs(dist_sum-bistatic_distance(i,j));
end
end
end
minimize( obj );
cvx_end
p_mse = x’;

But this yields

Disciplined convex programming error:
Illegal operation: abs( {convex} ).

How to solve this? Many thanks!

2

Something of the form abs(abs(p)-D) with p being the variable and D \ne 0, is not convex, as will more complicated variants thereof, such as yours.

3

so can’t be solved with CVX?

4

You’d have to introduce binary variables in order to handle the non-convexity. It might get rather messy.