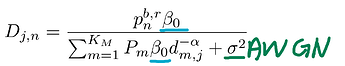CVX Failed in convex problem

Eric · October 21, 2024, 2:08pm

Hi there!

I’m currently working on the problem of max(theta) (without considering constraint 32c).
If anyone could lend a hand, I’d really appreciate the help. Thanks a lot in advance!
BTW I’m using cvx_solver mosek

 % cvx variable
  expression R_in_lb(K_U)   % Uplink
  variable theta              nonnegative
  variable Q_sub2(N, 2)       nonnegative
  variable H_sub2(N, 1)       nonnegative
  variable L_sub2(K_U, N)     nonnegative
  variable I_sub2(N, 1)       nonnegative
  variable d_slack_mn(K_M, N) nonnegative  % eq32f - 29
  
  % eq 32a
  maximize(theta)              % obj func

Problem max(theta)

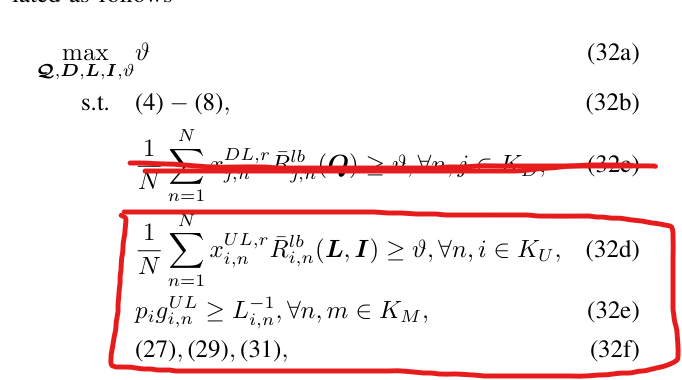
However, due to the constraint which I highlighted in the red box, cvx_status keeps telling me cvx_failed, even though `R^{lb}_{in}` has solution (for n = 1~4).

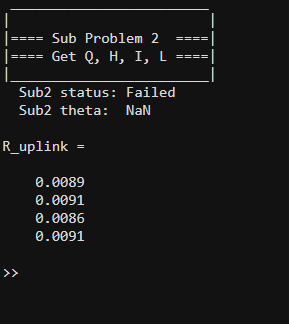
If I comment out max(theta) , cvx_status shows Infeasible

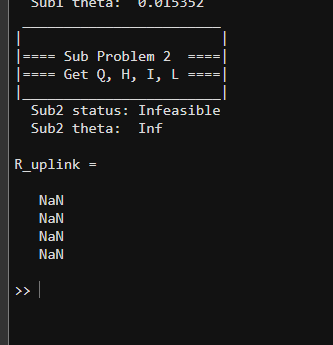
Full Output

Solver: Mosek
 _______________________ 
|                       |
|Iteration: 1 
|_______________________|
 _______________________ 
|                       |
|==== Sub Problem 1  ===|
|==== Get x_DL, x_UL ===|
|_______________________|
  Sub1 status: Solved
  Sub1 theta:  0.015352
 ________________________ 
|                        |
|==== Sub Problem 2  ====|
|==== Get Q, H, I, L ====|
|________________________|
 
Calling Mosek 10.2.5: 4684 variables, 2039 equality constraints
   For improved efficiency, Mosek is solving the dual problem.
------------------------------------------------------------

MOSEK Version 10.2.5 (Build date: 2024-9-17 14:14:12)
Copyright (c) MOSEK ApS, Denmark WWW: mosek.com
Platform: Windows/64-X86

Problem
  Name                   :                 
  Objective sense        : minimize        
  Type                   : CONIC (conic optimization problem)
  Constraints            : 2039            
  Affine conic cons.     : 0               
  Disjunctive cons.      : 0               
  Cones                  : 958             
  Scalar variables       : 4684            
  Matrix variables       : 0               
  Integer variables      : 0               

Optimizer started.
Presolve started.
Linear dependency checker started.
Linear dependency checker terminated.
Eliminator started.
Freed constraints in eliminator : 354
Eliminator terminated.
Eliminator started.
Freed constraints in eliminator : 0
Eliminator terminated.
Eliminator - tries                  : 2                 time                   : 0.00            
Lin. dep.  - tries                  : 1                 time                   : 0.00            
Lin. dep.  - primal attempts        : 1                 successes              : 1               
Lin. dep.  - dual attempts          : 0                 successes              : 0               
Lin. dep.  - primal deps.           : 0                 dual deps.             : 0               
Presolve terminated. Time: 0.02    
Optimizer  - threads                : 16              
Optimizer  - solved problem         : the primal      
Optimizer  - Constraints            : 842             
Optimizer  - Cones                  : 950             
Optimizer  - Scalar variables       : 3446              conic                  : 2783            
Optimizer  - Semi-definite variables: 0                 scalarized             : 0               
Factor     - setup time             : 0.00            
Factor     - dense det. time        : 0.00              GP order time          : 0.00            
Factor     - nonzeros before factor : 5240              after factor           : 7691            
Factor     - dense dim.             : 0                 flops                  : 1.71e+05        
ITE PFEAS    DFEAS    GFEAS    PRSTATUS   POBJ              DOBJ              MU       TIME  
0   1.0e+00  1.1e+06  2.5e+03  0.00e+00   2.536994000e+03   0.000000000e+00   1.0e+00  0.02  
1   4.6e-01  5.0e+05  1.7e+03  -1.00e+00  2.538185089e+03   2.485832545e+00   4.6e-01  0.02  
2   1.5e-01  1.6e+05  9.9e+02  -1.00e+00  2.533471954e+03   2.269832836e+00   1.5e-01  0.02  
3   2.5e-02  2.7e+04  4.0e+02  -1.00e+00  2.498447971e+03   1.182234896e+00   2.5e-02  0.02  
4   5.7e-03  6.1e+03  1.9e+02  -1.00e+00  2.359593471e+03   -5.219090421e-01  5.7e-03  0.02  
5   1.6e-03  1.8e+03  1.0e+02  -9.98e-01  1.919233521e+03   -2.323672323e-01  1.6e-03  0.02  
6   1.2e-03  1.3e+03  8.8e+01  -9.94e-01  1.702519265e+03   -2.782325771e-01  1.2e-03  0.02  
7   6.3e-04  6.8e+02  6.3e+01  -9.92e-01  9.635862008e+02   -3.646206056e-01  6.3e-04  0.02  
8   4.0e-04  4.3e+02  5.0e+01  -9.84e-01  5.533175603e+01   -4.193672396e-01  4.0e-04  0.02  
9   2.3e-04  2.5e+02  3.7e+01  -9.75e-01  -1.688914767e+03  -4.680444305e-01  2.3e-04  0.02  
10  1.1e-04  1.2e+02  2.6e+01  -9.58e-01  -5.593970113e+03  -5.148880246e-01  1.1e-04  0.03  
11  3.7e-05  4.0e+01  1.4e+01  -9.19e-01  -1.950931847e+04  -5.278844913e-01  3.7e-05  0.03  
12  9.8e-06  1.1e+01  5.7e+00  -7.76e-01  -5.062973413e+04  -4.537014592e-01  9.8e-06  0.03  
13  1.5e-06  1.6e+00  8.9e-01  -3.42e-01  -5.390332546e+04  -1.975171077e-01  1.5e-06  0.03  
14  1.8e-07  1.9e-01  3.9e-02  6.73e-01   -7.214396753e+03  -2.519808404e-02  1.8e-07  0.03  
15  1.9e-08  2.0e-02  1.0e-03  1.07e+00   -4.595046181e+02  -6.980631560e-04  1.9e-08  0.03  
16  1.9e-09  2.0e-03  3.1e-05  1.14e+00   -4.218889355e+01  1.705618431e-03   1.9e-09  0.03  
17  8.7e-10  9.4e-04  1.1e-05  8.99e-01   -2.473710351e+01  1.819864409e-03   8.7e-10  0.03  
18  6.5e-10  7.1e-04  1.1e-05  2.89e-02   -4.454728913e+01  1.772967400e-03   6.5e-10  0.03  
19  3.0e-10  3.2e-04  6.6e-06  -1.40e-01  -7.616190574e+01  1.755592886e-03   3.0e-10  0.03  
20  2.7e-10  2.0e-04  5.1e-06  -6.05e-01  -1.123551924e+02  1.732430259e-03   1.9e-10  0.03  
21  2.7e-10  2.0e-04  5.0e-06  -7.55e-01  -1.150418469e+02  1.730995792e-03   1.8e-10  0.05  
22  2.7e-10  2.0e-04  5.0e-06  -7.55e-01  -1.150418469e+02  1.730995792e-03   1.8e-10  0.05  
23  2.7e-10  2.0e-04  5.0e-06  -7.55e-01  -1.150418469e+02  1.730995792e-03   1.8e-10  0.05  
24  2.4e-10  2.0e-04  5.0e-06  -7.48e-01  -1.150622206e+02  1.730979808e-03   1.8e-10  0.05  
25  2.4e-10  2.0e-04  5.0e-06  -7.48e-01  -1.150622206e+02  1.730979808e-03   1.8e-10  0.05  
26  2.4e-10  2.0e-04  5.0e-06  -7.48e-01  -1.150622206e+02  1.730979808e-03   1.8e-10  0.06  
Optimizer terminated. Time: 0.06    


Interior-point solution summary
  Problem status  : UNKNOWN
  Solution status : UNKNOWN
  Primal.  obj: -1.1506222059e+02   nrm: 2e+07    Viol.  con: 4e-04    var: 3e-01    cones: 8e-05  
  Dual.    obj: 1.7309798076e-03    nrm: 2e+06    Viol.  con: 0e+00    var: 2e+02    cones: 0e+00  
Optimizer summary
  Optimizer                 -                        time: 0.06    
    Interior-point          - iterations : 27        time: 0.06    
      Basis identification  -                        time: 0.00    
        Primal              - iterations : 0         time: 0.00    
        Dual                - iterations : 0         time: 0.00    
        Clean primal        - iterations : 0         time: 0.00    
        Clean dual          - iterations : 0         time: 0.00    
    Simplex                 -                        time: 0.00    
      Primal simplex        - iterations : 0         time: 0.00    
      Dual simplex          - iterations : 0         time: 0.00    
    Mixed integer           - relaxations: 0         time: 0.00    

------------------------------------------------------------
Status: Failed
Optimal value (cvx_optval): NaN
 
  Sub2 status: Failed
  Sub2 theta:  NaN

R_uplink =

    0.0089
    0.0091
    0.0086
    0.0091

>>

eq (4~8), are all CONVEX

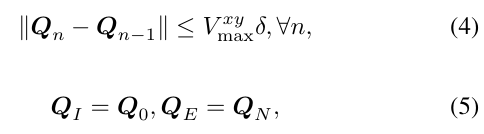
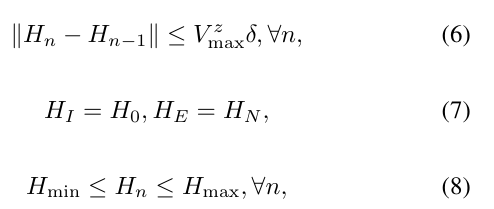
eq32d

For eq (32d) which applying inequality(34) to get lower bound, which is CONVEX

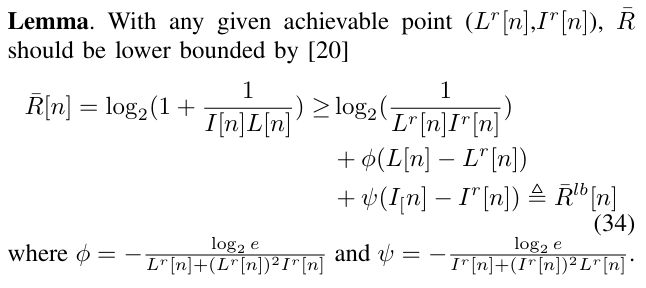
Hence, we can get the lowerbound of transmittion rate eq(26), which also appear in 32d

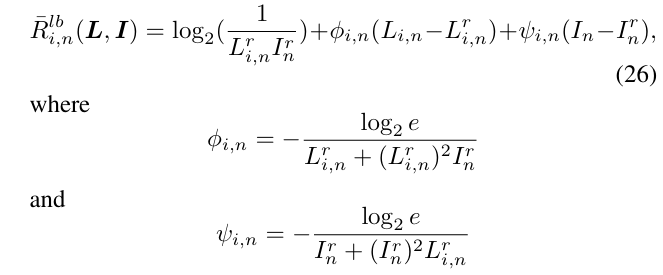
    % eq 32d 
    for i = 1:K_U
        R_in_lb(i) = 0;
        for n = 1:N  % eq 26: Uplink lower bound
            R_in_lb(i) = R_in_lb(i)+ x_UL_new(i,n)* (R_eq26_part1(i,n)+ R_eq26_part2(i,n)*(L_sub2(i, n)-L_riter(i, n))+ R_eq26_part3(i,n)*(I_sub2(n)-I_riter(n))); 
        end
        R_in_lb(i) = R_in_lb(i) / (N*log(2));
        R_in_lb(i) >= theta; % eq 32d
    end

eq 32e is CONVEX

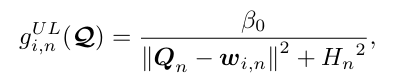
% eq 32e: L is directly proportional to d
for i = 1:K_U
    for n = 1:N
        L_sub2(i, n) >= (square_pos( norm(Q_sub2(n, :) - ULU_pos(i, :)) ) + power(H_sub2(n), 2)) / (P_max * beta_0);
    end
end

eq(27, 29, 31)

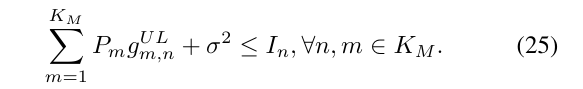
  % eq 32f - 27: I is inversely proportional to d
  for n = 1:N
      I_sub2(n) >= sum(P_max .* beta_0 .* inv_pos(d_slack_mn(:, n))) + AWGN;  % SUM m = 1 ~ K_m
  end

  % eq 32f - 31 
  for m = 1:K_M
      for n = 1:N   % 0 <= d_slack <= eq(30)
          0 <= d_slack_mn(m, n) <= (Q_jam_r2(m, n)+ H_r2(n) ...
              +2*(Q_riter(n, :) - jammer_pos(m, :))*(Q_sub2(n, :)-Q_riter(n, :)).'+ 2*H_riter(n)*(H_sub2(n) - H_riter(n)));    % eq 31
      end
  end

Full Code

function [Q_riter, H_riter, I_riter, L_riter, d_riter, theta_sub2] = subproblem2(Q_riter, H_riter, L_riter, I_riter, x_DL_new ,x_UL_new, ...
    beta_0, alpha, d_mj, P_max, ULU_pos, DLU_pos, jammer_pos, AWGN, N, delta, K_D, K_U, K_M, Q_ini, Q_end, V_xy_max, V_z_max, H_ini, H_end, H_min, H_max)

% Const Start ==============================
    H_r2 = zeros(N, 1);
    for n = 1:N
        H_r2(n) = power(H_riter(n), 2);
    end


    % Uplink ==================================================================================================================  
    R_eq26_part1= zeros(K_U, N);
    R_eq26_part2= zeros(K_U, N);
    R_eq26_part3= zeros(K_U, N);
    Q_ulu_r2 = zeros(K_U, N);
    for i= 1:K_U
       for n= 1:N

           R_eq26_part1(i,n)= log(1/(L_riter(i,n)*I_riter(n)));
           R_eq26_part2(i,n)= -1/(L_riter(i,n)+power(L_riter(i,n),2)*I_riter(n));
           R_eq26_part3(i,n)= -1/(I_riter(n)+power(I_riter(n),2)*L_riter(i,n));
           
           Q_ulu_r2(i,n) = square_pos( norm(Q_riter(n, :) - ULU_pos(i, :)) );

       end
    end
    
    Q_jam_r2 = zeros(K_M, N);
    for m = 1:K_M
        for n =1:N

            Q_jam_r2(m,n) = square_pos( norm(Q_riter(n, :) - jammer_pos(m, :)) );
            
        end
    end
%Const End ==============================

% CVX Start =================================================
    cvx_clear
    cvx_begin quiet
        % cvx_precision low
        expression R_in_lb(K_U)   % Uplink

        variable theta              nonnegative
        variable Q_sub2(N, 2)       nonnegative
        variable H_sub2(N, 1)       nonnegative
        variable L_sub2(K_U, N)     nonnegative
        variable I_sub2(N, 1)       nonnegative
        variable d_slack_mn(K_M, N) nonnegative  % eq32f - 29
    
        % eq 32a
        maximize(theta)              % obj func
            
        subject to
            % eq 32b
            for n = 2:N
                norm(Q_sub2(n,:) - Q_sub2(n-1,:)) <= V_xy_max * delta;   % eq 32b - eq 4
                norm(H_sub2(n) - H_sub2(n-1))     <= V_z_max  * delta;   % eq 32b - eq 6
            end                 
            Q_sub2(1, :) == Q_ini;            % eq 32b - eq 5
            Q_sub2(N, :) == Q_end;            % eq 32b - eq 5
            H_sub2(1)    == H_ini;            % eq 32b - eq 7
            H_sub2(N)    == H_end;            % eq 32b - eq 7
            H_min   <= H_sub2(:) <= H_max;    % eq 32b - eq 8
    
 

    %% Uplink Still can't solve==================================================================================================================  
            % eq 32d 
            for i = 1:K_U
                R_in_lb(i) = 0;
                for n = 1:N  % eq 26: Uplink lower bound
                    R_in_lb(i) = R_in_lb(i)+ x_UL_new(i,n)* (R_eq26_part1(i,n)+ R_eq26_part2(i,n)*(L_sub2(i, n)-L_riter(i, n))+ R_eq26_part3(i,n)*(I_sub2(n)-I_riter(n))); 
                end
                R_in_lb(i) = R_in_lb(i) / (N*log(2));
                R_in_lb(i) >= theta; % eq 32d
            end

            % eq 32e: L is directly proportional to d
            for i = 1:K_U
                for n = 1:N
                    L_sub2(i, n) >= (square_pos( norm(Q_sub2(n, :) - ULU_pos(i, :)) ) + power(H_sub2(n), 2)) / (P_max * beta_0);
                end
            end

            % eq 32f - 27: I is inversely proportional to d
            for n = 1:N
                I_sub2(n) >= sum(P_max .* beta_0 .* inv_pos(d_slack_mn(:, n))) + AWGN;  % SUM m = 1 ~ K_m
            end

            % eq 32f - 31 
            for m = 1:K_M
                for n = 1:N   % 0 <= d_slack <= eq(30)
                    0 <= d_slack_mn(m, n) <= (Q_jam_r2(m, n)+ H_r2(n) ...
                        +2*(Q_riter(n, :) - jammer_pos(m, :))*(Q_sub2(n, :)-Q_riter(n, :)).'+ 2*H_riter(n)*(H_sub2(n) - H_riter(n)));    % eq 31
                end
            end
    % Uplink ================================================================================================================== 
    
    cvx_end
% CVX end =================================================

    disp(['  Sub2 status: ', cvx_status])
    disp(['  Sub2 theta:  ', num2str(cvx_optval)])
    theta_sub2 = cvx_optval;
    % Update Q, H, L, I
    Q_riter     = Q_sub2;
    H_riter     = H_sub2;
    L_riter     = L_sub2;
    I_riter     = I_sub2;
    d_riter     = d_slack_mn;
    % R_downlink  = R_jn_lb
    R_uplink    = R_in_lb
    
    save('data\Q_riter.mat', 'Q_riter'); 
    save('data\H_riter.mat', 'H_riter'); 
    save('data\L_riter.mat', 'L_sub2'); 
    save('data\I_riter.mat', 'I_sub2'); 
    save('data\d_riter.mat', 'd_slack_mn');
    % save('data\R_downlink.mat', 'R_downlink');
    save('data\R_uplink.mat', 'R_uplink');
end

Mark_L_Stone · October 21, 2024, 4:01pm

First of all, don’t use quiet;.Then you will see all the CVX and solver output. You can edit your post to add the output. Mosek displays diagnostic information, which Mosek developers who read the forum can help assess. Pay attention to any warnings Mosek might issue.

Also see, Debugging infeasible models - YALMIP , all of which, except for section 1, also applies to CVX.

Eric · October 22, 2024, 6:34am

Thank you!
I’ve just added the full output in my previous post, and I’m currently reviewing the website you recommended.

Mark_L_Stone · October 22, 2024, 11:45am

Mosek didn’t issue explicit warnings, but the large norm reported by Mosek suggests that perhaps the input data scaling is not good, with some values perhaps larger in magnitude than desired. That may be contributing to Mosek’s difficulty solving the problem with a reliable determination (Mosek status of UNKNOWN). Try changing choice of units to make all non-zero input data within a few orders of magnitude of 1. Once the scaling is good, then you can hopefully get a more reliable determination of whether the problem is actually infeasible.

Eric · October 22, 2024, 1:15pm

Hi, Sir,

I have been trying to rescale the values.
Could you recommend a range of scaling factors between AWGN and β_0?

Also, since eq(26e) requires a feasible point for L_riter and I_riter, could you also recommend a range for these parameters?

Initial Parameter

AWGN      = 10^(-14);    % sigma^2
beta_0    = 10^(-9);     % channel gian(60dbm) %10^(-9); 
scale     = 10^(13);     % scaling factor , keep the ratio between noise & path gain 
AWGN      = AWGN    *scale;
beta_0    = beta_0  *scale; 

%%%% Initial L_riter, I_riter for sub2======================
L_riter    = 1 *ones(K_U, N); 
I_riter    = 1 *ones(N, 1);

With the current parameters, I am able to obtain the following results, but it still shows Infeasible.
Thank you!

Output

===Clean data=== 
Solver: Mosek
 _______________________ 
|                       |
|Iteration: 1 
|_______________________|
 _______________________ 
|                       |
|==== Sub Problem 1  ===|
|==== Get x_DL, x_UL ===|
|_______________________|
  Sub1 status: Solved
  Sub1 theta:  0.015352
 ________________________ 
|                        |
|==== Sub Problem 2  ====|
|==== Get Q, H, I, L ====|
|________________________|
 
Calling Mosek 10.2.5: 4684 variables, 2039 equality constraints
   For improved efficiency, Mosek is solving the dual problem.
------------------------------------------------------------

MOSEK Version 10.2.5 (Build date: 2024-9-17 14:14:12)
Copyright (c) MOSEK ApS, Denmark WWW: mosek.com
Platform: Windows/64-X86

Problem
  Name                   :                 
  Objective sense        : minimize        
  Type                   : CONIC (conic optimization problem)
  Constraints            : 2039            
  Affine conic cons.     : 0               
  Disjunctive cons.      : 0               
  Cones                  : 958             
  Scalar variables       : 4684            
  Matrix variables       : 0               
  Integer variables      : 0               

Optimizer started.
Presolve started.
Linear dependency checker started.
Linear dependency checker terminated.
Eliminator started.
Freed constraints in eliminator : 0
Eliminator terminated.
Eliminator - tries                  : 1                 time                   : 0.00            
Lin. dep.  - tries                  : 1                 time                   : 0.00            
Lin. dep.  - primal attempts        : 1                 successes              : 1               
Lin. dep.  - dual attempts          : 0                 successes              : 0               
Lin. dep.  - primal deps.           : 0                 dual deps.             : 0               
Presolve terminated. Time: 0.00    
Optimizer  - threads                : 16              
Optimizer  - solved problem         : the primal      
Optimizer  - Constraints            : 783             
Optimizer  - Cones                  : 950             
Optimizer  - Scalar variables       : 3387              conic                  : 2783            
Optimizer  - Semi-definite variables: 0                 scalarized             : 0               
Factor     - setup time             : 0.01            
Factor     - dense det. time        : 0.00              GP order time          : 0.00            
Factor     - nonzeros before factor : 5122              after factor           : 7457            
Factor     - dense dim.             : 0                 flops                  : 1.70e+05        
ITE PFEAS    DFEAS    GFEAS    PRSTATUS   POBJ              DOBJ              MU       TIME  
0   1.0e+00  1.1e+06  7.5e+03  0.00e+00   -7.463006000e+03  0.000000000e+00   1.0e+00  0.01  
1   4.6e-01  5.0e+05  5.1e+03  -1.00e+00  -7.460756172e+03  3.650307666e+00   4.6e-01  0.01  
2   1.5e-01  1.6e+05  2.9e+03  -1.00e+00  -7.465364007e+03  3.359769549e+00   1.5e-01  0.01  
3   2.5e-02  2.7e+04  1.2e+03  -1.00e+00  -7.498520295e+03  2.744001772e+00   2.5e-02  0.01  
4   4.8e-03  5.2e+03  5.2e+02  -1.00e+00  -7.659670184e+03  2.337061182e+00   4.8e-03  0.01  
5   1.6e-03  1.7e+03  2.9e+02  -9.98e-01  -8.073214397e+03  1.380619975e+00   1.6e-03  0.01  
6   1.1e-03  1.2e+03  2.5e+02  -9.94e-01  -8.293487348e+03  1.185655217e+00   1.1e-03  0.01  
7   6.4e-04  7.0e+02  1.9e+02  -9.91e-01  -8.932259667e+03  8.750470809e-01   6.4e-04  0.01  
8   4.0e-04  4.3e+02  1.5e+02  -9.85e-01  -9.789155727e+03  6.647154333e-01   4.0e-04  0.01  
9   2.3e-04  2.5e+02  1.1e+02  -9.76e-01  -1.145554010e+04  4.685736615e-01   2.3e-04  0.01  
10  1.1e-04  1.2e+02  7.6e+01  -9.59e-01  -1.525065692e+04  2.464946203e-01   1.1e-04  0.01  
11  3.4e-05  3.7e+01  3.9e+01  -9.22e-01  -2.981527648e+04  -5.902248654e-02  3.4e-05  0.01  
12  1.0e-05  1.1e+01  1.8e+01  -7.78e-01  -5.743265143e+04  -4.491620831e-01  1.0e-05  0.01  
13  6.1e-06  6.6e+00  1.2e+01  -5.04e-01  -7.023310669e+04  -4.885065976e-01  6.1e-06  0.01  
14  3.2e-06  3.4e+00  7.6e+00  -5.39e-01  -1.074072523e+05  -4.740184062e-01  3.2e-06  0.01  
15  6.7e-07  7.2e-01  3.3e+00  -7.26e-01  -4.396401530e+05  -4.858405251e-01  6.7e-07  0.03  
16  1.1e-07  1.2e-01  1.3e+00  -9.38e-01  -2.573647657e+06  -4.855250964e-01  1.1e-07  0.03  
17  2.6e-08  2.8e-02  6.2e-01  -9.84e-01  -1.054907481e+07  -4.860237668e-01  2.6e-08  0.03  
18  6.3e-09  6.8e-03  3.0e-01  -1.00e+00  -4.163583536e+07  -4.901658974e-01  6.3e-09  0.03  
Optimizer terminated. Time: 0.03    


Interior-point solution summary
  Problem status  : DUAL_INFEASIBLE
  Solution status : DUAL_INFEASIBLE_CER
  Primal.  obj: -4.8400447040e-01   nrm: 3e+01    Viol.  con: 6e-06    var: 0e+00    cones: 3e-09  
Optimizer summary
  Optimizer                 -                        time: 0.03    
    Interior-point          - iterations : 18        time: 0.03    
      Basis identification  -                        time: 0.00    
        Primal              - iterations : 0         time: 0.00    
        Dual                - iterations : 0         time: 0.00    
        Clean primal        - iterations : 0         time: 0.00    
        Clean dual          - iterations : 0         time: 0.00    
    Simplex                 -                        time: 0.00    
      Primal simplex        - iterations : 0         time: 0.00    
      Dual simplex          - iterations : 0         time: 0.00    
    Mixed integer           - relaxations: 0         time: 0.00    

------------------------------------------------------------
Status: Infeasible
Optimal value (cvx_optval): -Inf
 
  Sub2 status: Infeasible
  Sub2 theta:  -Inf

R_uplink =

   NaN
   NaN
   NaN
   NaN

>>

Mark_L_Stone · October 22, 2024, 2:19pm

I don’t know what your attempted scaling is doing, but you shouldn’t just change one number without making other changes as needed in your model to keep it making sense. For instance, use nm instead of meters, and picovolts instead of volts, etc. You should try to get input data, by the time it makes it into a CVX expression (not counting any numerical calculations done by MATLAB before CVX sees the data (such as inside parentheses in a purely numerical expression)), to be within a magnitude span of about 1e-3 to 1e3 iif possible. Certainly not beyond 1e-6 to 1e6 (but that’s pretty bad).

Once your numerical data is ‘good":, Mosek’;s feasibility determination should be more reliable, and you can follow the rest of the advice in the links.

Eric · October 22, 2024, 2:36pm

Got it, thank you sir!
Also, I want to ask about what does DUAL_INFEASIBLE mean, which I posted in the previous reply?

Interior-point solution summary
  Problem status  : DUAL_INFEASIBLE
  Solution status : DUAL_INFEASIBLE_CER

full output

===Clean data=== 
Solver: Mosek
 _______________________ 
|                       |
|Iteration: 1 
|_______________________|
 _______________________ 
|                       |
|==== Sub Problem 1  ===|
|==== Get x_DL, x_UL ===|
|_______________________|
  Sub1 status: Solved
  Sub1 theta:  0.015352
 ________________________ 
|                        |
|==== Sub Problem 2  ====|
|==== Get Q, H, I, L ====|
|________________________|
 
Calling Mosek 10.2.5: 4684 variables, 2039 equality constraints
   For improved efficiency, Mosek is solving the dual problem.
------------------------------------------------------------

MOSEK Version 10.2.5 (Build date: 2024-9-17 14:14:12)
Copyright (c) MOSEK ApS, Denmark WWW: mosek.com
Platform: Windows/64-X86

Problem
  Name                   :                 
  Objective sense        : minimize        
  Type                   : CONIC (conic optimization problem)
  Constraints            : 2039            
  Affine conic cons.     : 0               
  Disjunctive cons.      : 0               
  Cones                  : 958             
  Scalar variables       : 4684            
  Matrix variables       : 0               
  Integer variables      : 0               

Optimizer started.
Presolve started.
Linear dependency checker started.
Linear dependency checker terminated.
Eliminator started.
Freed constraints in eliminator : 0
Eliminator terminated.
Eliminator - tries                  : 1                 time                   : 0.00            
Lin. dep.  - tries                  : 1                 time                   : 0.00            
Lin. dep.  - primal attempts        : 1                 successes              : 1               
Lin. dep.  - dual attempts          : 0                 successes              : 0               
Lin. dep.  - primal deps.           : 0                 dual deps.             : 0               
Presolve terminated. Time: 0.00    
Optimizer  - threads                : 16              
Optimizer  - solved problem         : the primal      
Optimizer  - Constraints            : 783             
Optimizer  - Cones                  : 950             
Optimizer  - Scalar variables       : 3387              conic                  : 2783            
Optimizer  - Semi-definite variables: 0                 scalarized             : 0               
Factor     - setup time             : 0.01            
Factor     - dense det. time        : 0.00              GP order time          : 0.00            
Factor     - nonzeros before factor : 5122              after factor           : 7457            
Factor     - dense dim.             : 0                 flops                  : 1.70e+05        
ITE PFEAS    DFEAS    GFEAS    PRSTATUS   POBJ              DOBJ              MU       TIME  
0   1.0e+00  1.1e+06  7.5e+03  0.00e+00   -7.463006000e+03  0.000000000e+00   1.0e+00  0.01  
1   4.6e-01  5.0e+05  5.1e+03  -1.00e+00  -7.460756172e+03  3.650307666e+00   4.6e-01  0.01  
2   1.5e-01  1.6e+05  2.9e+03  -1.00e+00  -7.465364007e+03  3.359769549e+00   1.5e-01  0.01  
3   2.5e-02  2.7e+04  1.2e+03  -1.00e+00  -7.498520295e+03  2.744001772e+00   2.5e-02  0.01  
4   4.8e-03  5.2e+03  5.2e+02  -1.00e+00  -7.659670184e+03  2.337061182e+00   4.8e-03  0.01  
5   1.6e-03  1.7e+03  2.9e+02  -9.98e-01  -8.073214397e+03  1.380619975e+00   1.6e-03  0.01  
6   1.1e-03  1.2e+03  2.5e+02  -9.94e-01  -8.293487348e+03  1.185655217e+00   1.1e-03  0.01  
7   6.4e-04  7.0e+02  1.9e+02  -9.91e-01  -8.932259667e+03  8.750470809e-01   6.4e-04  0.01  
8   4.0e-04  4.3e+02  1.5e+02  -9.85e-01  -9.789155727e+03  6.647154333e-01   4.0e-04  0.01  
9   2.3e-04  2.5e+02  1.1e+02  -9.76e-01  -1.145554010e+04  4.685736615e-01   2.3e-04  0.01  
10  1.1e-04  1.2e+02  7.6e+01  -9.59e-01  -1.525065692e+04  2.464946203e-01   1.1e-04  0.01  
11  3.4e-05  3.7e+01  3.9e+01  -9.22e-01  -2.981527648e+04  -5.902248654e-02  3.4e-05  0.01  
12  1.0e-05  1.1e+01  1.8e+01  -7.78e-01  -5.743265143e+04  -4.491620831e-01  1.0e-05  0.01  
13  6.1e-06  6.6e+00  1.2e+01  -5.04e-01  -7.023310669e+04  -4.885065976e-01  6.1e-06  0.01  
14  3.2e-06  3.4e+00  7.6e+00  -5.39e-01  -1.074072523e+05  -4.740184062e-01  3.2e-06  0.01  
15  6.7e-07  7.2e-01  3.3e+00  -7.26e-01  -4.396401530e+05  -4.858405251e-01  6.7e-07  0.03  
16  1.1e-07  1.2e-01  1.3e+00  -9.38e-01  -2.573647657e+06  -4.855250964e-01  1.1e-07  0.03  
17  2.6e-08  2.8e-02  6.2e-01  -9.84e-01  -1.054907481e+07  -4.860237668e-01  2.6e-08  0.03  
18  6.3e-09  6.8e-03  3.0e-01  -1.00e+00  -4.163583536e+07  -4.901658974e-01  6.3e-09  0.03  
Optimizer terminated. Time: 0.03    


Interior-point solution summary
  Problem status  : DUAL_INFEASIBLE
  Solution status : DUAL_INFEASIBLE_CER
  Primal.  obj: -4.8400447040e-01   nrm: 3e+01    Viol.  con: 6e-06    var: 0e+00    cones: 3e-09  
Optimizer summary
  Optimizer                 -                        time: 0.03    
    Interior-point          - iterations : 18        time: 0.03    
      Basis identification  -                        time: 0.00    
        Primal              - iterations : 0         time: 0.00    
        Dual                - iterations : 0         time: 0.00    
        Clean primal        - iterations : 0         time: 0.00    
        Clean dual          - iterations : 0         time: 0.00    
    Simplex                 -                        time: 0.00    
      Primal simplex        - iterations : 0         time: 0.00    
      Dual simplex          - iterations : 0         time: 0.00    
    Mixed integer           - relaxations: 0         time: 0.00    

------------------------------------------------------------
Status: Infeasible
Optimal value (cvx_optval): -Inf
 
  Sub2 status: Infeasible
  Sub2 theta:  -Inf

R_uplink =

   NaN
   NaN
   NaN
   NaN

>>

Mark_L_Stone · October 22, 2024, 2:43pm

Mosek was provided the dual of the original problem by CVX. Therefore, Mosek’s determination of dual infeasible corresponds to primal infeasible for your original problem/ CVX accounts for this, and therefore reported the status as infeasible (meaning primal infeasible).