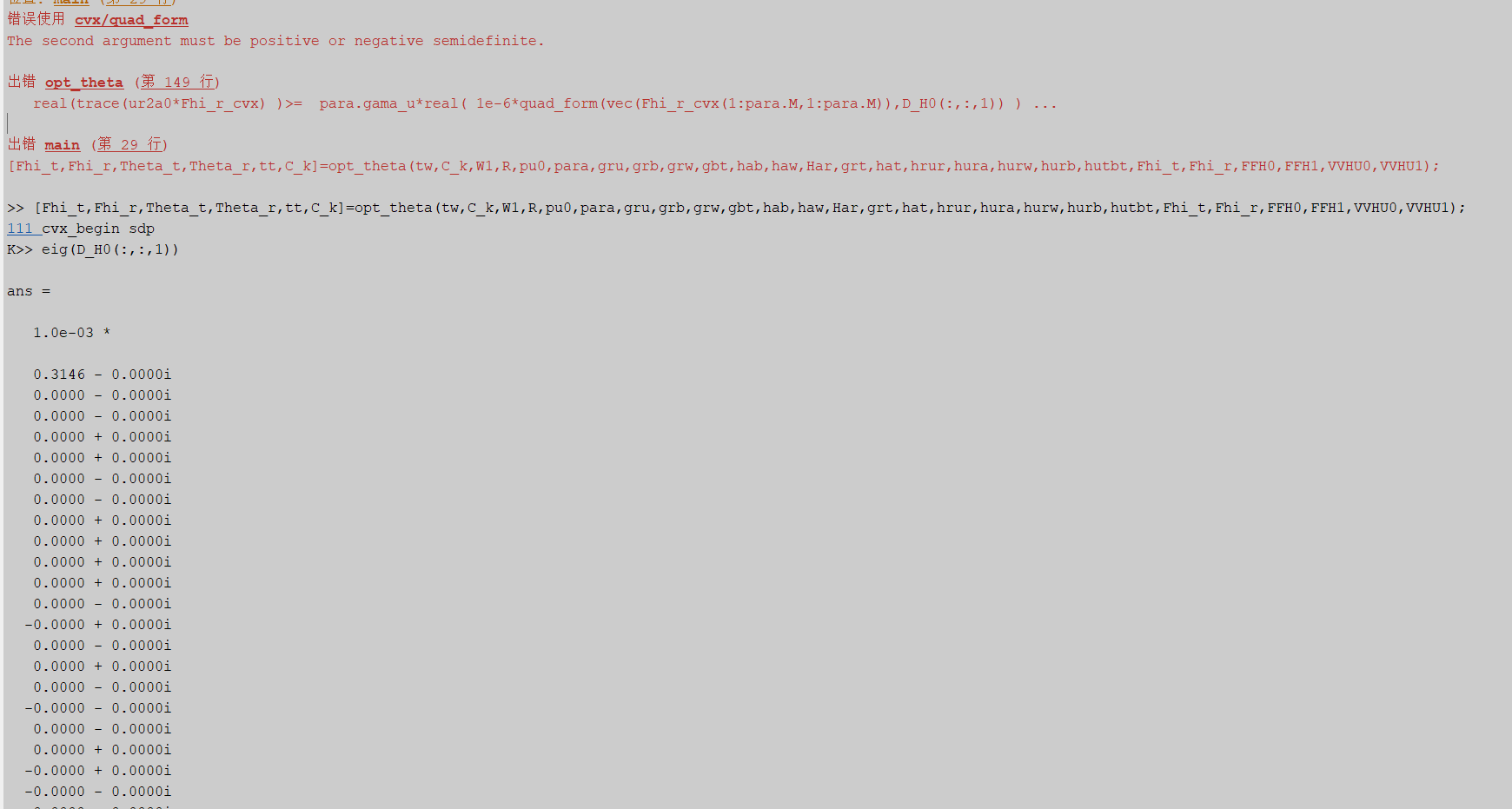
CVX’s conclusion is correct. The matrix is numerically indefinite. There are roundoff level negative eigenvalues, which perhaps would be exactly zero if the matrix were constructed in exact arithmetic. There appears to also be roundoff level imaginary terms.
Symmetrizing the matrix by replacing
D_Ho(:,:,1) with 0.5*(D_Ho(:,:,1) + D_Ho(:,:,1)') will hopefully eliminate the imaginary term. As for the roundoff level negative eigenvalues, either construct the matrix in a more careful manner, or perhaps add a small multiple of the Identity matrix to D_Ho(:,:,1) , which will make all the eigenvalues computationally positive.
Also, the 1e-6 multiplicative factor appears indicative of poor numerical scaling, and is likely a rather poor way of dealing with it.