Recently, the following problems have been encountered when using the CVX toolbox :
Only quadratic scalar forms can be specified in CVX
The objective function contains X * X ', where X is a complex vector of 10 * 1, how to solve it?
That’s a non-convex bilinear expression. If there is any hope of using CVX, you’d have to provide context to see whether there is a reformulation which works for it. But first carefully read
including the part about proving your problem is convex.
Thank you very much for your reply,Mark.The context as following:
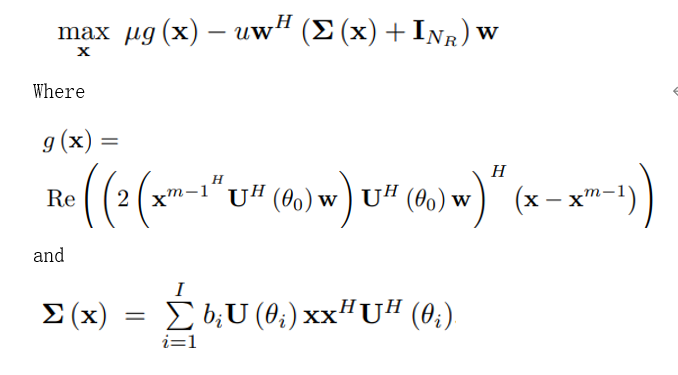
To tell the truth,I don’t sure if it can be solved by CVX.But the paper says it can be solved by CVX toolbox.So I hope to get your help.Thank you most sincerely
Use the fact that
U*x*x'*U' = square_pos(norm(U*x))
I have tried, but it is wrong : the function ’ square _ poa ’ corresponding to the input parameter of type ’ cvx ’ is not defined. What can I do to solve it?
You can wait for me to correct the typo, which I just did.
Ok, waiting for you.
Ok, I see what you modified, but there is still an error : the operand must be a real number. Is that because the variable X is plural ? Or there will be other reasons?
Please provide reproducible code, complete with all input data, which exhibits the error. You probably have some inputs or other code which don’
t make sense.
clear
%% 初始化
NT=10; %发射天线数
NR=10; %接收天线数
K=5; %单天线通信用户总数
L=1; %传播路径数
P0=30; %功率分配
vk=1; %莱斯分布系数
m_max=10; %最大迭代次数,假设为10
epsilong=1;
alpha0=sqrt(5)+sqrt(5)*1i;
theta=[0 -50 -20 20 50]; %目标位置和杂波源位置
I=length(theta); %杂波源总数
alpha1=sqrt(10)+sqrt(10)*1i;
[alpha2,alpha3,alpha4]=deal(alpha1);
Gamma_T=-1; %信噪比阈值
Gamma_k=15; %信噪比阈值
sigma_R=1;
sigma_Ck=1;
ommiga_k1=[0 -50 -20 20 50];
ommiga_k0=[-90 -45 0 45 90]; %假设出发角均匀分布
%ommiga_k1=[-90 -45 0 45 90]; %假设出发角均匀分布
z=normrnd(0,sigma_R,1,10); %噪声 生成均值为零,标准差为sigma_R的1*10随机数矩阵
nk=normrnd(0,sigma_Ck); %噪声 生成均值为零,标准差为sigma_Ck的正态分布随机变量
A=[exp((pi/4)*1j),exp((3*pi/4)*1j),exp((5*pi/4)*1j),exp((7*pi/4)*1j)]; %诱导符号集
%% 雷达信号模型
at_theta=zeros(NT,K);
ar_theta=zeros(NR,K);
b=((abs(alpha1))^2)/sigma_R;
miu=((abs(alpha0))^2)/sigma_R;
for k=1:K
at_theta(:,k)=(1/sqrt(NT))*[1 exp(-1j*pi*sind(theta(k))) exp(-1j*2*pi*sind(theta(k))) exp(-1j*3*pi*sind(theta(k))) exp(-1j*4*pi*sind(theta(k))) exp(-1j*5*pi*sind(theta(k))) exp(-1j*6*pi*sind(theta(k))) exp(-1j*7*pi*sind(theta(k))) exp(-1j*8*pi*sind(theta(k))) exp(-1j*9*pi*sind(theta(k)))]';
ar_theta(:,k)=(1/sqrt(NR))*[1 exp(-1j*pi*sind(theta(k))) exp(-1j*2*pi*sind(theta(k))) exp(-1j*3*pi*sind(theta(k))) exp(-1j*4*pi*sind(theta(k))) exp(-1j*5*pi*sind(theta(k))) exp(-1j*6*pi*sind(theta(k))) exp(-1j*7*pi*sind(theta(k))) exp(-1j*8*pi*sind(theta(k))) exp(-1j*9*pi*sind(theta(k)))]';
U{k}=ar_theta(:,k)*at_theta(:,k)'; %注意:U{1}表示U0
end
%% 通信信号模型
at_ommiga=zeros(NT,K);
ommiga=zeros(K,5);
at_ommigakl=zeros(NT,K);
h_LOS=zeros(NT,K);
h_NLOS=zeros(NT,K);
h=zeros(NT,K);
c=zeros(K,1);
for k=1:K
at_ommiga(:,k)=(1/sqrt(NT))*[1 exp(-1j*pi*sind(ommiga_k0(k))) exp(-1j*2*pi*sind(ommiga_k0(k))) exp(-1j*3*pi*sind(ommiga_k0(k))) exp(-1j*4*pi*sind(ommiga_k0(k))) exp(-1j*5*pi*sind(ommiga_k0(k))) exp(-1j*6*pi*sind(ommiga_k0(k))) exp(-1j*7*pi*sind(ommiga_k0(k))) exp(-1j*8*pi*sind(ommiga_k0(k))) exp(-1j*9*pi*sind(ommiga_k0(k)))].';
at_ommigakl(:,k)=(1/sqrt(NT))*[1 exp(-1j*pi*sind(ommiga_k1(k))) exp(-1j*2*pi*sind(ommiga_k1(k))) exp(-1j*3*pi*sind(ommiga_k1(k))) exp(-1j*4*pi*sind(ommiga_k1(k))) exp(-1j*5*pi*sind(ommiga_k1(k))) exp(-1j*6*pi*sind(ommiga_k1(k))) exp(-1j*7*pi*sind(ommiga_k1(k))) exp(-1j*8*pi*sind(ommiga_k1(k))) exp(-1j*9*pi*sind(ommiga_k1(k)))].';
c(k,1)=sqrt(1/2)*(randn(1,1)+1j*randn(1,1)); %生成均值为0 方差为1的复高斯分布
h_LOS(:,k)=sqrt(NT)*at_ommiga(:,k); %视距传输
h_NLOS(:,k)=sqrt(NT/L)*c(k,1)*at_ommigakl(:,k); %非视距传输
h(:,k)=sqrt(vk/(1+vk))*h_LOS(:,k)+sqrt(1/(1+vk))*h_NLOS(:,k); %信道矢量
end
%% 优化目标函数
x_he=zeros(10,10);
m=1;
x0=[1-1i;1+1i;1-1i;1-1i;1-1i;1-1i;1-1i;1+1i;1-1i;1-1i].'; %随机x0
x(:,1)=x0;
AI=eye(10); %10*10单位矩阵
while m<=m_max
for i=1:4
x_he=x_he+b*U{i+1}*x(:,m)*x(:,m)'*U{i+1}';
end
U1=U{2}+U{3}+U{4}+U{5};
U2=U{2}'+U{3}'+U{4}'+U{5}';
cvx_begin
variable X(10) complex %定义复数向量X
w(:,m)=(inv(x_he+AI)*U{1}*x(:,m))/(x(:,m)'*U{1}'*inv(x_he+AI)*U{1}*x(:,m)); %更新w
u=(miu*((abs(w(:,m)'*U{1}*x(:,m)))^2))/(w(:,m)'*(x_he+AI)*w(:,m)); %更新u
% f1=(2*(x(:,m)'*U{1}'*w(:,m))*U{1}'*w(:,m))';
% f2=miu*real((2*(x(:,m)'*U{1}'*w(:,m))*U{1}'*w(:,m))'*x(:,m));
% f3=(u*w(:,m)'*(b*U1*X*X1*U2)*w(:,m));
% f4=(u*w(:,m)'*AI*w(:,m));
maximize(miu*(real((2*(x(:,m)'*U{1}'*w(:,m))*U{1}'*w(:,m))'*(X-x(:,m))))-(u*w(:,m)'*((b*square_pos(norm(U1*X))+AI)*w(:,m)))) %目标函数
subject to
square_pos(norm(X,2))<=P0; %约束条件 式(12b)
for k=1:K
i=unidrnd(4); %产生1到4之间的随机正整数
s(k)=A(1);
abs(imag(h(:,k)'*X*conj(s(k))))<=((real(h(:,k)'*X*conj(s(k))))-sqrt(sigma_Ck*Gamma_k))*tand(-45); %约束条件 式(12c)
end
cvx_end
SINR_rad(m)=cvx_optval;
m=m+1;
x(:,m)=X;
end
figure(1)
plot(SINR_rad,'-+b')
xlabel('迭代次数m');
ylabel('SINR_r_a_d(dB)');
title('收敛性分析');
grid onw(:,m) is complex, and it is multiplying the convex expression, square_pos(norm(U1*X)) which is not allowed by CVX because it can’t determine its convexity.
Your code basically has w(:,m)'*convex_expression*w(:,m)
A solution is to change it to convex_expression*(w(:,m)'*w(:,m)) or (w(:,m)'*w(:,m))*convex_expression. That way, there will be a nonnegative real scalar number multiplying the convex_expression, which will make CVX happy.
U1 is a matrix of 10*10,and X is a vector of 10 * 1, so the result of U1 * X * X ’ * U1 ’ should be a matrix of 10 * 10 , but the result of square _ pos ( norm ( U1 * X ) ) is a scalar, which is not true. Is there any other expression that can solve this problem?
Use square_pos(norm(X'*U1'*w)) in place of w'*U*X*X'*U1'*w)
There is still error :Cannot perform the operation: {complex affine} .* {convex}.Is there any solution?
Where is the error occurring? Please show the complete current version of your code.
This transformation seems to cause a change in the dimensions of the matrix, for example, if convex_expression is N x N and w is N x M, then w ’ * convex-expression * w is M x M, but convex-expression * (w (:, m)’ * w (:, m)) does not satisfy matrix multiplication
If convex expression is not scalar, I suggested using square_pos(norm(X'*U1'*w)) in place of w'*U*X*X'*U1'*w