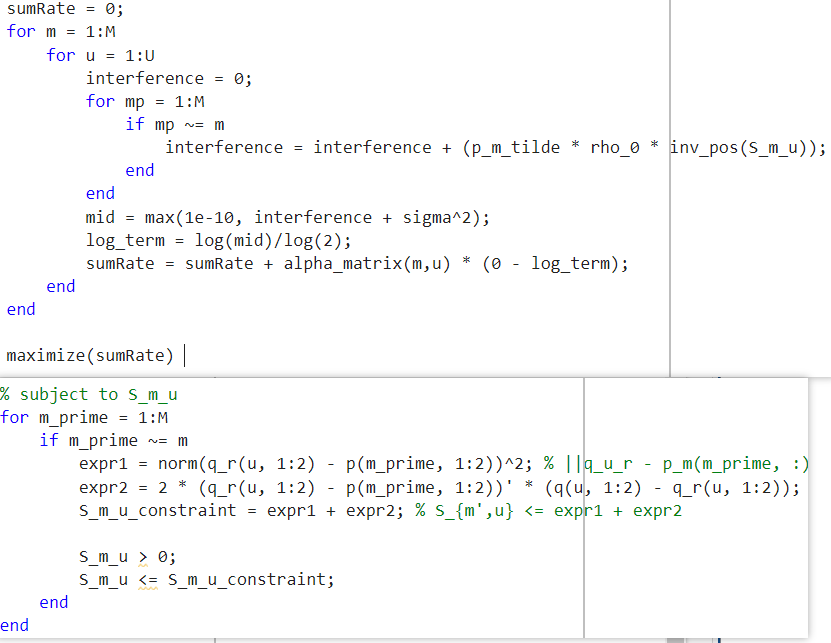
However, I keep encountering the error: “The number or type of inputs or outputs for function log2 is incorrect.” When I switch to the form log(interference)/log(2), another error occurs.
“cvx/log
Disciplined convex programming error:
Illegal operation: log( {convex} ).”
I tried removing inv_pos(S_m_u) from the interference expression, and it ran without errors. However, when I add it back, it causes errors.
This looks like log-sum-inv, which you can search for in this forum Search results for 'log-sum-inv' - CVX Forum: a community-driven support forum. Or see Log( {convex} ) , among other posts for how to implement section 5.2.7 Log-sum-inv of Mosek Modeling Cookbook in CVX.
Mark, thank you very much for your valuable guidance.
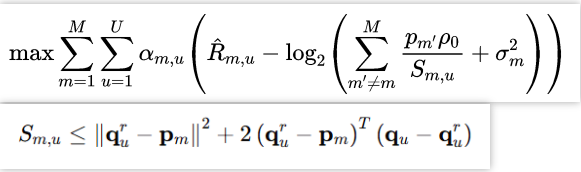
I have a follow-up question regarding my optimization problem. The optimization variable is q, while R_hat_m_u and S_m_u are functions of q. I am currently focusing on the part involving −log 2(). Specifically, in the constraints related to S_m_u, only q_u (not q_u_r) is a variable; the other components are constants.
I looked at other related posts on the forum, and this post Log( {convex} ) is quite similar to mine. However, my optimization objective is closer to the form t = log(1/x1+...+1/xn) in section 5.2.7 log-sum-inv,rather than the inequality form. Therefore, is the following formulation correct?
variables t y(n) x(n)
maximize(t)
subject to
1 ./ x <= exp(y); % Element-wise constraint 1/x_i <= exp(y_i)
t <= log_sum_exp(y); % log_sum_exp computes log(exp(y1) + ... + exp(yn))
cvx_end
That won’t work.
But I think the following would work if there weren’t a double summation over m and u in the objective. i.e for a fixed value of m and u. Note how I adjusted my formulation to match what is in section 5.2.7 of the Mosek cookbook.
t >= log_sum_exp([y;log(sigma_squared)])
x./(p*rho) >= exp(-y)
And use t/log(2) in place of the log2 term.
But because of the double summation, you’re going to need to add 2 dimensions (one dimension for each of m and u) to each of t, x, and y, and make the appropriate adjustments. I’ll leave the details of the indexing to you.
I don’t understand why double summation might have an impact that causes it not to work. Can’t I use log-sum-inv to represent the log2() part separately, then subtract the expression of R_hat, and solve the problem with a double for loop?
Regarding the adjustment to section 5.2.7, I have a question: If I am optimizing t=log(1/x1+...+1/xn) , rather than t≥log(1/x1+...+1/xn) , should I still use maximize(t)?
or just
cvx_begin
variables t y(n) x
maximize(t)
subject to
t == log_sum_exp(y)
x == exp(-y)
cvx_end
The same scalar variables can’t be used different times for different terms or indices.
So,
variables t(M,U) x(n,M,U) y(n,M,U)
or something. As I said, I leave the details of the indexing to you.
Perhaps you don’t need any for loops at all if you properly vectorize. For instance,
help log_sum_exp
log_sum_exp log(sum(exp(x))).
log_sum_exp(X) = LOG(SUM(EXP(X)).When used in a CVX model, log_sum_exp(X) causes CVX's successive approximation method to be invoked, producing results exact to within the tolerance of the solver. This is in contrast to LOGSUMEXP_SDP, which uses a single SDP-representable global approximation. If X is a matrix, LOGSUMEXP_SDP(X) will perform its computations along each column of X. If X is an N-D array, LOGSUMEXP_SDP(X) will perform its computations along the first dimension of size other than 1. LOGSUMEXP_SDP(X,DIM) will perform its computations along dimension DIM. Disciplined convex programming information: log_sum_exp(X) is convex and nondecreasing in X; therefore, X must be convex (or affine).
The code using for loops might be more straightforward to write, but will take longer for CVX to process (formulate) the model.
The t (or each component of it) is used in place of the original log term. The reason it works, despite use of the inequality constraint t >= ... rather than an equality constraint, is that the process of optimization forces the inequality to be satisfied with equality at optimality, provided that t is used in a “convex” fashion, which it is in this case. That is the whole basis for this reformulation “trick”, and many others. The inequality constraint is convex and allowed in convex optimization (and CVX), but nonlinear equality constraint is not allowed in convex optimization (or CVX). So we “trick” CVX by providing it an inequality constraint, knowoing that it will be satisfied with equality at optimality.
Sorry, Mark. I might be a bit slow, but I understood what you mentioned about the double summation. However, I still don’t quite grasp the part about optimizing t=log(1/x1+...+1/xn). Could you please point out where my logic is wrong?
If my code logic is as you provided:
cvx_begin
variables t y(n) x
maximize(t)
subject to
t >= log_sum_exp([y; log(sigma_squared)])
x./(p*rho) >= exp(-y)
cvx_end
It’s clear that t has a lower bound, but since we are maximizing t, theoretically, t could be +∞. However, this is obviously not valid, and it seems that this setup is not equivalent to optimizing
maximize(t=log(1/x1+...+1/xn))
Why can’t the code be written like this?
cvx_begin
variables t y(n) x
maximize(t)
subject to
t <= log_sum_exp([y;log(sigma_squared)])
x./(p*rho) >= exp(-y)
cvx_end
Since 1/xi <= exp(yi), the constraint t <= log_sum_exp([y;log(sigma_squared)]) is valid. Thus, t has an upper bound, which aligns with our optimization goal of maximize(t).
If my code logic is incorrect, how should I write it? Besides that, it seems I haven’t seen the “details of the indexing” you mentioned. Should I be looking for this somewhere specific?
It seems that the log-sum-exp function operates from 1 to n. If I have an intermediate n'≠n, how can I handle this using log-sum-exp ?
——————————————— Second revision —————————————————
I am now trying to use log-sum-inv. I didn’t use log-sum-exp, but that seems to work as well. I want to first run a result. I used the product of pho and p as gamma. The updated code is as follows, but it shows an Disciplined convex programming error: Illegal operation: {convex} - {convex} message.
cvx_begin
variable q(U, 3)
variable S_m_u
variable y
expression sumRate
sumRate = 0;
for m = 1:M
for u = 1:U
interference = 0;
for mp = 1:M
if mp ~= m
interference = interference + exp(y);
end
end
interference = interference + sigma^2;
log_term = log(interference)/log(2);
R_hat_m_u = 0;
for j = 1:M
norm_diff = pow_pos(norm(q(u, 1:2) - p(j, 1:2)),2) - pow_pos(norm(q_r(u, 1:2) - p(j, 1:2)),2);
R_hat_m_u = R_hat_m_u + norm_diff;
end
sumRate = sumRate + alpha_matrix(m,u) * (R_hat_m_u - log_term);
end
end
maximize(sumRate)
subject to
for u = 1:U
% subject to S_m_u
for m_prime = 1:M
if m_prime ~= m
expr1 = norm(q_r(u, 1:2) - p(m_prime, 1:2))^2;
expr2 = 2 * (q_r(u, 1:2) - p(m_prime, 1:2))' * (q(u, 1:2) - q_r(u, 1:2));
S_m_u_constraint = expr1 + expr2;
S_m_u > 0;
S_m_u <= S_m_u_constraint;
exp(-y) <= S_m_u/gamma;
end
end
end
How should I resolve this?
Your code
cvx_begin
variables t y(n) x
maximize(t)
subject to
t >= log_sum_exp([y; log(sigma_squared)])
x./(p*rho) >= exp(-y)
cvx_end
is wrong because it should be -t which is maximized. That is because there is -log in the objective function. As I wrote earlier, t replaces the log term… So -log becomes -t. That should resolve your paradox. Given that resolution, I won’t attempt to assess the remainder of your post, except for indexing.
As for indexing, I just mean you need to set things up, same as in “regular” MATLAB, to make sure the correct terms are included in your sums, with all the indices being correct for the various CVX and MATLAB (input data) variables.
Thank you for your generous guidance.
Another way of looking at it, as I wrote earlier, is that t needs to be used in a convex fashion. Maximizing -t is in a convex fashion. Maximizing t is not in a convex fashion.