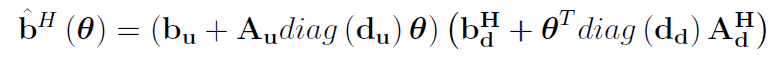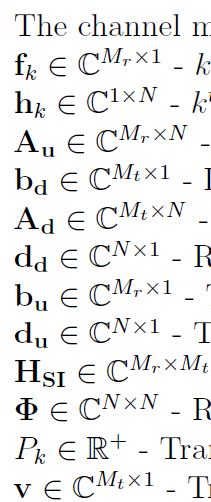ˆf(𝜽) = f + A𝑢diag (h) 𝜽, will norm(ˆf(𝜽) )^2 is convex or not?
If everything other than \theta (or the additive f) is input data, f(\theta) is affine; therefore norm((f(\theta)) is convex and is allowed by CVX, and square_pos(norm(f(\theta))) is also convex and is allowed by CVX.
If something other than \theta or f s an optimization variable, or some function (expression) of optimization variables, then we would need to know what those exact relations are in order to make that determination.
In the future, you should be telling whether something is convex, not asking us, as discussed in Why isn't CVX accepting my model? READ THIS FIRST! .
p= (b + a diag(d)𝜽)* (x + 𝜽^T diag(e)y), will norm(p*g)^2 is convex or not? Remember that all are in matrix/vector form and dimensions are perfect?
At this point, I don’t even know what the expressions is you are trying to analyze. You are showing some kind of pseudo math, pseudo code, which is neither. Perhaps there are \theta multiplying each other, which would be non-affine, but I can’t tell.
If you want help, you will need to write things out clearly. You also need to read the previously provided link, and follow its guidance.
and the following one is Convex or Non-convex?
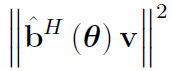
The following are the dimensions of the above mentioned terms:
And also
As far as I can tell, that is non-convex. But is up to you to prove or disprove convexity, as is clearly stated in the link above - perhaps you can now invest the time to read it?
The paper says that this is non-convex and I also verified this by taking some example (By considering some order values, N and Mt, Mr).
Hence the equation reduces to two variable and then calculate the hessian matrix also.
After that Eigen values are calculated and hence it is found that it is not a PSD . Hence it is Non-convex.
But my concert here is that "How to calculate whether given function with matrix/vector variables is convex or not without taking some assumptions like order values?
Can we calculate hessian matrix directly? Plz answer this Sir
So this is non-convex, and CVX can’;t be used to enter or solve it.
To learn more about determining convexity and convex optimization, you can read and solve exercises in the first 3 to 5 chapters of Convex Optimization – Boyd and Vandenberghe . And f you need help with that, perhaps seek it at https://math.stackexchange.com/ .
If you are looking for a MATLAB-based tool which can handle convex and non-convex optimization problems, you can try YALMIP.
Please read and FOLLOW the advice in the previously provided link, Why isn't CVX accepting my model? READ THIS FIRST! before posting again on this forum.
Yes Sir. I have gone through your post regarding convexity or non-convexity and how CVX will deal with it as well.
Thanks for the clarification sir. I will try to refer to the Boyd text book for further clarification.
Thanks