{convex} ./ {real affine}

1

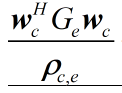
image
image
how to deal with this problem?

2

help quad_over_lin

quad_over_lin Sum of squares over linear.
Z=quad_over_lin(X,Y), where X is a vector and Y is a scalar, is equal to
SUM(ABS(X).^2)./Y if Y is positive, and +Inf otherwise. Y must be real.

If X is a matrix, quad_over_lin(X,Y) is a row vector containing the values
of quad_over_lin applied to each column. If X is an N-D array, the operation
is applied to the first non-singleton dimension of X.

quad_over_lin(X,Y,DIM) takes the sum along the dimension DIM of X.
A special value of DIM == 0 is accepted here, which is automatically
replaced with DIM == NDIMS(X) + 1. This has the effect of eliminating
the sum; thus quad_over_lin( X, Y, NDIMS(X) + 1 ) = ABS( X ).^2 ./ Y.

In all cases, Y must be compatible in the same sense as ./ with the squared
sum; that is, Y must be a scalar or the same size as SUM(ABS(X).^2,DIM).

Disciplined convex programming information:
    quad_over_lin is convex, nonmontonic in X, and nonincreasing in Y.
    Thus when used with CVX expressions, X must be convex (or affine)
    and Y must be concave (or affine).
3

So how do I use quad_over_lin to represent my expression, quad_over_lin(a,b) = (a^2)/b, but I have a conjugate transpose matrix Ge in the middle

4

quad_over_lin(sqrtm(Ge*wc,rho_ce)

7

Do you want to express quad_over_lin(sqrtm(wc’Ge wc),rho_ce)?
One more question, how do I represent 2^x, x is a variable, direct representation seems to lead to NAN error, do I need to use the built-in function to cvx to represent this

8

quad_over_lin(sqrtm(Ge*wc,rho_ce) can be used for wc'*Ge*wc/eho_ce

As for you “one more question”, please show a complete reproducible problem, with all input, and with all solver and CVX output. if the problem is determined to be infeasible, unbounded, or the solver has numerical difficulties, the variables might be populated with NaN.