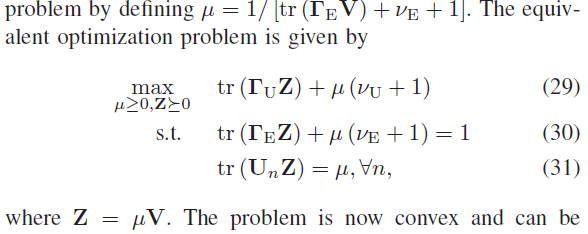A problem is described in the snapshot. I have to optimize it using the CVX tool. all the entries are given but i am having a problem because it has to be maximized over two variables Z and u. kindly some one help me how to defined multiple variable to solve this problem, Z= complex and u= double data type.
can I apply alternate optimization here, in ist step solve for Z and for u separately?
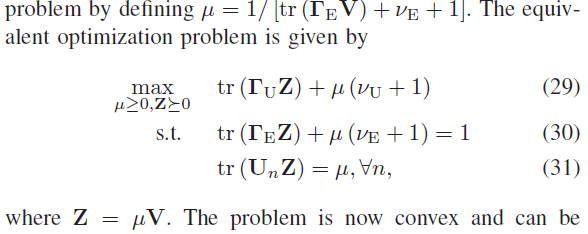
CVX allows as many variable declarations as you want, either as separate variable statements, or in some circumstances, as described at http://cvxr.com/cvx/doc/basics.html#variables in a single variables statement.
It would be a good idea for you to read or re-rad the enitire CVX Users’ Guide.
1 Like
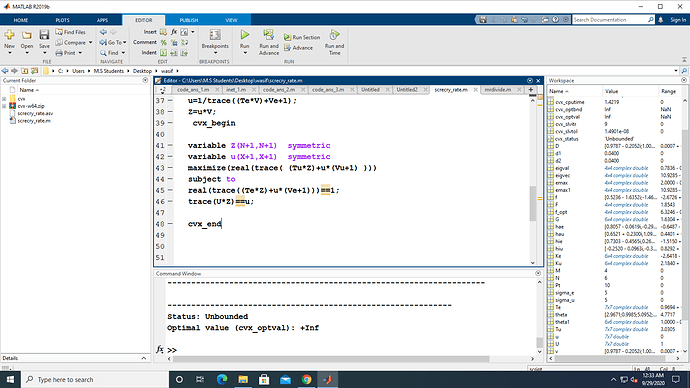
can you help me with this, my cvx prog =m is giving +infinity
variable Z(N+1,N+1) symmetric
variable u(X+1,X+1) symmetric
maximize(real(trace( (Tu*Z)+u*(Vu+1) )))
subject to
real(trace((Te*Z)+u*(Ve+1)))=1;
trace(U*Z)=u;
cvx_end
The CVX output clearly states the problem is unbounded.
If you are trying to implement the model in the first post, you need to constrain Z and u to be semidefinite. The easiest way is to change symmetric to semidefinite in the variable declarations. Is u (\mu) supposed to be a scalar? I’ll let you figure that out, it’s “your” model, in the sense that you got it out of a paper or book. Semidefinite for a scalar just means nonnegative, as apparently the constraint on it is intended to be.
The equality constraints must use == not =. The program as written has assignments, not equality constrains. Actually, I would expect real(trace((Te*Z)+u*(Ve+1)))=1;and trace(U*Z)=u; to produce error messages. However, the image you show has ==, not = That bespeaks a lack of care in preparing your post, which does not serve the cause of minimizing the time and effort required for forum readers to help you.
If that doesn’t cure the unboundedneess, then
follow the advice at the following link. it also applies to CVX. https://yalmip.github.io/debuggingunbounded/
thanks for your constant help, sorry i forgot to update the code in the post. I have to change the var from symmetric to complex semidefinite and its working, but still, it is not converging the way I need it.