Conditions on indexes of a matrix

1

Hello. How can I impose a condition like this on indexes of matrix A in CVX? I want to sum over all elements such that row+column = constant and make this sum equal to zero.
Sigma({A}_{i,j}) = 0, i+j = constant.

2

I don’t find your question to be clear. Can you write out explicitly the constraints you want for a small matrix, such as 3 by 3?

3

Thanks for your answer. In the following, I clearly explain the problem.
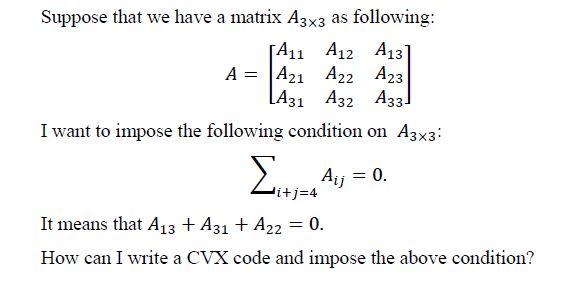
CVX problem

4

You are apparently trying to constrain the sum of the skew-diagonal

sum(diag(fliplr(A))) == 0

1 Like
5

Thanks a lot! And how can I generalize the above problem to the following problem by CVX?
CVX2

6

You ought to be able to specify kt’h diagonals using diag, and of course index into submatrices using A(1:3,1:3), and also use fliplr. So perhaps you can combine them to do what you want. CVX allows you to use for loops. I’ll leave the details to you as an exercise.

help diag

diag Diagonal matrices and diagonals of a matrix.
diag(V,K) when V is a vector with N components is a square matrix
of order N+ABS(K) with the elements of V on the K-th diagonal. K = 0
is the main diagonal, K > 0 is above the main diagonal and K < 0
is below the main diagonal.

diag(V) is the same as diag(V,0) and puts V on the main diagonal.

diag(X,K) when X is a matrix is a column vector formed from
the elements of the K-th diagonal of X.

diag(X) is the main diagonal of X. diag(diag(X)) is a diagonal matrix.

Example
   m = 5;
   diag(-m:m) + diag(ones(2*m,1),1) + diag(ones(2*m,1),-1)
produces a tridiagonal matrix of order 2*m+1.
1 Like
7

Thanks for your attention and guidance!

8

sum(diag(fliplr(A))) == 0
can be written more simply as
trace(fliplr(A)) == 0
although this simpler form doesn’t generalize to the more general form in your follow-up question.

1 Like
9

Thank you so much. My CVX code worked a long time ago with your suggestion.