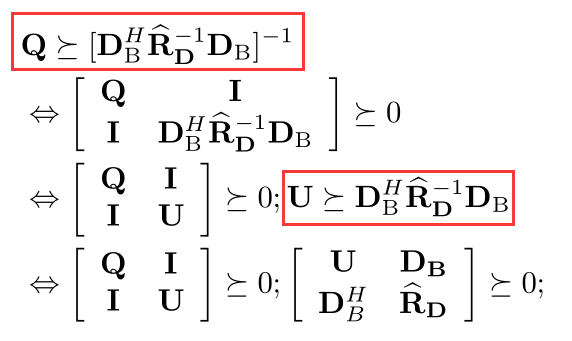Complex-value SDP， status: Inaccurate/Solved

1446324166 · May 10, 2021, 7:11am

Hello，there. Recently I met a complex-value SDP(See Fig1) and I have written an example, in order to fulfil the CVX requirement, I transform the complex cost function Q d_z d_z^H to the real from.

Fig 1865×546 40 KB

Here is the code:
cvx_begin sdp

variable Q(37,37) complex
variable U(37,37) complex
variable D_B(37,16) complex

% minimize( real(trace(Q * d * d’)) )
minimize( trace([real(Q * d * d’) imag(Q * d * d’);…
imag(Q * d * d’) real(Q * d * d’) ] ) )
[Q eye(37); …
eye(37) U ] >= 0;
[U D_B;… D_B’ H{1}’ * H{1} ] >= 0;
norm( covar.^0.5 *(D_B - H{1}), ‘fro’ ) <= sqrt(epsilon);
cvx_end

Here is the results obtained by the CVX toolbox (a powerful tool ), below is the information in the command window, What I pay attention to is the solution status: Inaccurate/Solved，Does this mean that the parameter ϵ need to be reselected to get accurate results? Are there any other reasons cause this problem?

Calling SDPT3 4.0: 9471 variables, 3923 equality constraints
For improved efficiency, SDPT3 is solving the dual problem.

num. of constraints = 3923
dim. of sdp var = 254, num. of sdp blk = 2
dim. of socp var = 1185, num. of socp blk = 1
dim. of linear var = 1

SDPT3: Infeasible path-following algorithms

version predcorr gam expon scale_data
HKM 1 0.000 1 0
it pstep dstep pinfeas dinfeas gap prim-obj dual-obj cputime

0|0.000|0.000|8.9e+02|2.4e+01|4.0e+05| 6.434428e+02 0.000000e+00| 0:0:00| spchol 1 1
1|0.934|0.749|5.9e+01|6.2e+00|3.5e+04| 5.212444e+02 -1.416297e+01| 0:0:01| chol 1 1
2|0.955|0.939|2.7e+00|4.6e-01|2.1e+03| 3.169193e+02 -1.622513e+01| 0:0:02| chol 1 1
3|0.959|0.970|1.1e-01|4.0e-02|1.4e+02| 5.243215e+01 -2.592914e+00| 0:0:03| chol 1 1
4|0.935|0.982|7.1e-03|3.4e-03|1.1e+01| 4.928957e+00 -7.687543e-02| 0:0:04| chol 1 1
5|0.797|0.871|1.5e-03|1.0e-03|2.5e+00| 1.081716e+00 -1.790940e-02| 0:0:05| chol 1 1
6|0.795|0.724|3.3e-04|4.1e-04|6.7e-01| 2.373968e-01 -9.965924e-03| 0:0:06| chol 1 2
7|0.760|0.484|8.7e-05|2.6e-04|2.6e-01| 5.759075e-02 -6.731366e-03| 0:0:07| chol 1 2
8|0.520|0.386|4.3e-05|1.7e-04|1.6e-01| 2.656444e-02 -4.793308e-03| 0:0:08| chol 1 2
9|0.574|0.156|1.9e-05|1.6e-04|1.1e-01| 1.099523e-02 -3.585860e-03| 0:0:09| chol 1 2
10|0.343|0.927|1.2e-05|1.5e-05|3.1e-02| 6.541681e-03 -3.032168e-03| 0:0:10| chol 1 2
11|0.800|0.250|2.5e-06|1.4e-05|1.3e-02| 9.740229e-04 -1.886401e-03| 0:0:11| chol 1 3
12|0.319|0.803|1.7e-06|3.2e-06|5.9e-03| 3.442704e-04 -1.016627e-03| 0:0:13| chol 1 3
13|0.693|0.273|5.1e-07|2.7e-06|2.7e-03|-1.635565e-04 -6.799737e-04| 0:0:14| chol 1 3
14|0.314|0.417|3.5e-07|1.6e-06|1.8e-03|-2.336975e-04 -4.622611e-04| 0:0:15| chol 3 4
15|0.217|0.188|2.8e-07|1.4e-06|1.5e-03|-2.361353e-04 -3.512294e-04| 0:0:16| chol 4 5
16|0.430|0.662|1.6e-07|5.3e-07|8.3e-04|-2.405661e-04 -2.957133e-04| 0:0:17| chol 7 8
17|0.197|0.358|1.3e-07|3.7e-07|6.7e-04|-2.382880e-04 -2.453147e-04| 0:0:19| chol 5 10
18|0.274|0.915|9.2e-08|5.7e-08|4.8e-04|-2.276927e-04 -2.029439e-04| 0:0:21| chol 12 15
19|0.161|1.000|7.7e-08|1.8e-08|4.7e-04|-2.172798e-04 -2.345466e-04| 0:0:23| chol 5 5
20|0.380|0.358|4.8e-08|2.7e-08|3.1e-04|-1.840339e-04 -1.450176e-04| 0:0:25| chol 12 19
21|0.446|1.000|2.7e-08|9.6e-09|1.9e-04|-1.582627e-04 -1.167336e-04| 0:0:27| chol
warning: symqmr failed: 0.3
switch to LU factor. lu 8 2
22|0.372|0.625|1.7e-08|8.9e-09|1.3e-04|-1.339103e-04 -8.191619e-05| 0:0:31| lu 11 30
23|0.264|0.465|1.2e-08|8.1e-09|9.3e-05|-1.202736e-04 -7.664034e-05| 0:0:35| lu 11 30
24|0.246|1.000|9.9e-09|2.5e-09|7.5e-05|-1.091676e-04 -7.630504e-05| 0:0:40| lu 30 30
25|0.095|0.795|9.2e-09|2.5e-09|7.2e-05|-1.057806e-04 -7.106540e-05| 0:0:45| lu 30 30
26|0.142|0.208|8.9e-09|3.8e-09|6.0e-05|-9.986526e-05 -6.208033e-05| 0:0:51| lu 16 30
27|0.025|0.031|9.2e-09|5.5e-09|5.7e-05|-9.869497e-05 -6.018876e-05| 0:0:55| lu 11 30
28|0.121|0.196|8.1e-09|6.2e-09|5.0e-05|-9.385943e-05 -5.314914e-05| 0:1:00| lu 30 30
29|0.008|0.016|8.5e-09|7.8e-09|4.9e-05|-9.351511e-05 -5.296758e-05| 0:1:05| lu 16 30
30|0.008|0.029|8.1e-09|9.2e-09|4.9e-05|-9.319807e-05 -5.258045e-05| 0:1:10|
stop: steps too short consecutively

number of iterations = 30
primal objective value = -9.31980730e-05
dual objective value = -5.25804496e-05
gap := trace(XZ) = 4.89e-05
relative gap = 4.89e-05
actual relative gap = -4.06e-05
rel. primal infeas (scaled problem) = 8.09e-09
rel. dual " " " = 9.24e-09
rel. primal infeas (unscaled problem) = 0.00e+00
rel. dual " " " = 0.00e+00
norm(X), norm(y), norm(Z) = 1.7e+01, 1.2e+04, 1.5e+04
norm(A), norm(b), norm© = 8.1e+01, 2.1e+00, 7.8e+00
Total CPU time (secs) = 69.68
CPU time per iteration = 2.32
termination code = -5
DIMACS: 1.5e-08 0.0e+00 4.8e-08 0.0e+00 -4.1e-05 4.9e-05

Status: Inaccurate/Solved
Optimal value (cvx_optval): +5.25804e-05

Mark_L_Stone · May 10, 2021, 11:41am

That means that the SPT3 solver could not obtain the desired accuracy. perhaps another solver, such as Mosek, could. It may be that numerically poorly scaled input data very large and/or small magnitude non-zero numbers, is contributing to the difficulty.

1446324166 · May 10, 2021, 12:43pm

Thanks for your reply :grinning, I have try to use the Mosek like that, and get the result:Status: Infeasible.

covar = eye(size(H{1},1));
epsilon = 1e-6;

% cvx_precision best % high? low ? medium
cvx_solver mosek
cvx_begin sdp

variable Q(37,37) complex
variable U(37,37) complex
variable D_B(37,16) complex

% minimize( real(trace(Q * d * d’)) )
minimize( trace([real(Q * d * d’) imag(Q * d * d’);…
imag(Q * d * d’) real(Q * d * d’) ] ) )
[Q eye(37); …
eye(37) U ] >= 0;
[U D_B;… D_B’ H{1}’ * H{1} ] >= 0;
norm( covar.^0.5 *(D_B - H{1}), ‘fro’ ) <= sqrt(epsilon);
cvx_end

and get the result:Status: Infeasible

Calling Mosek 9.1.9: 9471 variables, 3923 equality constraints
For improved efficiency, Mosek is solving the dual problem.

MOSEK Version 9.1.9 (Build date: 2019-11-21 11:34:40)
Copyright © MOSEK ApS, Denmark. WWW: mosek.com
Platform: Windows/64-X86

Problem
Name :
Objective sense : min
Type : CONIC (conic optimization problem)
Constraints : 3923
Cones : 1
Scalar variables : 1186
Matrix variables : 2
Integer variables : 0

Optimizer started.
Presolve started.
Linear dependency checker started.
Linear dependency checker terminated.
Eliminator started.
Freed constraints in eliminator : 0
Eliminator terminated.
Eliminator - tries : 1 time : 0.00
Lin. dep. - tries : 1 time : 0.00
Lin. dep. - number : 0
Presolve terminated. Time: 0.01
Problem
Name :
Objective sense : min
Type : CONIC (conic optimization problem)
Constraints : 3923
Cones : 1
Scalar variables : 1186
Matrix variables : 2
Integer variables : 0

Optimizer - threads : 4
Optimizer - solved problem : the primal
Optimizer - Constraints : 3922
Optimizer - Cones : 1
Optimizer - Scalar variables : 1185 conic : 1185
Optimizer - Semi-definite variables: 2 scalarized : 16697
Factor - setup time : 0.56 dense det. time : 0.00
Factor - ML order time : 0.16 GP order time : 0.00
Factor - nonzeros before factor : 6.07e+06 after factor : 6.07e+06
Factor - dense dim. : 2 flops : 1.17e+10
ITE PFEAS DFEAS GFEAS PRSTATUS POBJ DOBJ MU TIME
0 4.0e+00 1.0e+00 1.2e+01 0.00e+00 1.075029164e+01 0.000000000e+00 1.0e+00 0.63
1 8.6e-01 2.1e-01 4.1e+00 -8.53e-01 3.495018759e+00 -1.796711256e+00 2.1e-01 1.20
2 1.7e-01 4.4e-02 5.1e-01 9.75e-02 -5.430604350e-01 -1.851203388e+00 4.4e-02 1.70
Optimizer terminated. Time: 1.73

Interior-point solution summary
Problem status : DUAL_INFEASIBLE
Solution status : DUAL_INFEASIBLE_CER
Primal. obj: -1.2057798334e-01 nrm: 1e+00 Viol. con: 2e-01 var: 0e+00 barvar: 0e+00 cones: 0e+00
Optimizer summary
Optimizer - time: 1.73
Interior-point - iterations : 2 time: 1.70
Basis identification - time: 0.00
Primal - iterations : 0 time: 0.00
Dual - iterations : 0 time: 0.00
Clean primal - iterations : 0 time: 0.00
Clean dual - iterations : 0 time: 0.00
Simplex - time: 0.00
Primal simplex - iterations : 0 time: 0.00
Dual simplex - iterations : 0 time: 0.00
Mixed integer - relaxations: 0 time: 0.00

Status: Infeasible
Optimal value (cvx_optval): +Inf

Mark_L_Stone · May 10, 2021, 12:58pm

Look at the input data scaling. Follow the advice at https://yalmip.github.io/debugginginfeasible , except for section 1.

Perhaps a very small value of epsilon is contributing to difficulty. Try increasing that and see what happens.

Mark_L_Stone · May 10, 2021, 1:14pm

Maybe you need to declare Q and U as complex hermitian.

1446324166 · May 10, 2021, 1:23pm

Thanks for your suggestions, I have declared Q and U as complex hermitian, also I adjust the solver precision.

cvx_precision medium %best % high? low ? medium
% cvx_solver mosek
cvx_begin sdp

variable Q(37,37) complex hermitian
variable U(37,37) complex hermitian
variable D_B(37,16) complex

% minimize( real(trace(Q * d * d’)) )
minimize( trace([real(Q * d * d’) imag(Q * d * d’);…
imag(Q * d * d’) real(Q * d * d’) ] ) )
[Q eye(37); …
eye(37) U ] >= 0;
[U D_B;… D_B’ H{1}’ * H{1} ] >= 0;
norm( covar.^0.5 *(D_B - H{1}), ‘fro’ ) <= sqrt(epsilon);
cvx_end

Here is the result: Status: Solved

Calling Mosek 9.1.9: 9471 variables, 3923 equality constraints
For improved efficiency, Mosek is solving the dual problem.

MOSEK Version 9.1.9 (Build date: 2019-11-21 11:34:40)
Copyright © MOSEK ApS, Denmark. WWW: mosek.com
Platform: Windows/64-X86

Problem
Name :
Objective sense : min
Type : CONIC (conic optimization problem)
Constraints : 3923
Cones : 1
Scalar variables : 1186
Matrix variables : 2
Integer variables : 0

Optimizer started.
Presolve started.
Linear dependency checker started.
Linear dependency checker terminated.
Eliminator started.
Freed constraints in eliminator : 0
Eliminator terminated.
Eliminator - tries : 1 time : 0.00
Lin. dep. - tries : 1 time : 0.00
Lin. dep. - number : 0
Presolve terminated. Time: 0.03
Problem
Name :
Objective sense : min
Type : CONIC (conic optimization problem)
Constraints : 3923
Cones : 1
Scalar variables : 1186
Matrix variables : 2
Integer variables : 0

Optimizer - threads : 4
Optimizer - solved problem : the primal
Optimizer - Constraints : 3922
Optimizer - Cones : 1
Optimizer - Scalar variables : 1185 conic : 1185
Optimizer - Semi-definite variables: 2 scalarized : 16697
Factor - setup time : 0.55 dense det. time : 0.00
Factor - ML order time : 0.16 GP order time : 0.00
Factor - nonzeros before factor : 6.07e+06 after factor : 6.07e+06
Factor - dense dim. : 2 flops : 1.17e+10
ITE PFEAS DFEAS GFEAS PRSTATUS POBJ DOBJ MU TIME
0 4.0e+00 1.0e+00 1.2e+01 0.00e+00 1.078091442e+01 0.000000000e+00 1.0e+00 0.63
1 8.5e-01 2.1e-01 4.1e+00 -8.53e-01 3.450716834e+00 -1.810695397e+00 2.1e-01 1.20
2 1.1e-01 2.7e-02 2.4e-01 1.11e-01 -9.303731649e-01 -1.733217328e+00 2.7e-02 1.78
3 6.3e-03 1.6e-03 3.4e-03 1.17e+00 -1.423387997e-01 -1.830590373e-01 1.6e-03 2.36
4 1.1e-03 2.7e-04 2.8e-04 8.68e-01 -5.537669385e-02 -6.188782836e-02 2.7e-04 2.89
5 1.7e-04 4.2e-05 2.2e-05 7.44e-01 -2.645045314e-02 -2.723537572e-02 4.2e-05 3.50
6 3.2e-05 8.1e-06 2.3e-06 5.51e-01 -1.756040827e-02 -1.770233324e-02 8.1e-06 4.08
7 5.3e-06 1.3e-06 2.8e-07 7.94e-02 -7.827966333e-03 -7.717110728e-03 1.3e-06 4.61
8 1.5e-06 3.8e-07 6.3e-08 5.05e-01 -4.997426540e-03 -4.888073631e-03 3.8e-07 5.20
9 5.2e-07 1.3e-07 1.7e-08 5.19e-01 -3.552141570e-03 -3.470225164e-03 1.3e-07 5.75
10 1.3e-07 3.1e-08 3.1e-09 4.39e-01 -2.219054936e-03 -2.165172129e-03 3.1e-08 6.36
11 2.9e-08 7.2e-09 5.0e-10 3.02e-01 -1.370240166e-03 -1.340397205e-03 7.2e-09 6.91
12 6.1e-09 1.5e-09 7.8e-11 2.23e-01 -7.889729774e-04 -7.724152117e-04 1.5e-09 7.59
13 1.4e-09 3.5e-10 1.3e-11 2.80e-01 -4.506254366e-04 -4.405945546e-04 3.4e-10 8.16
14 3.4e-10 1.5e-10 2.5e-12 3.36e-01 -2.718409410e-04 -2.658648290e-04 8.5e-11 8.91
15 7.5e-11 7.2e-11 4.1e-13 3.55e-01 -1.664255088e-04 -1.630508473e-04 1.9e-11 9.45
16 1.7e-11 4.6e-10 7.2e-14 2.62e-01 -1.010381683e-04 -9.901119761e-05 4.3e-12 9.98
17 3.9e-12 4.1e-10 1.3e-14 2.62e-01 -6.069352252e-05 -5.944296667e-05 9.6e-13 10.72
18 4.0e-13 8.3e-10 1.0e-15 2.75e-01 -3.240464962e-05 -3.173581567e-05 1.1e-13 12.30
19 5.7e-14 1.0e-08 1.1e-16 1.40e-01 -1.784600698e-05 -1.751477956e-05 1.6e-14 13.02
20 1.9e-14 6.1e-09 3.0e-17 1.35e-01 -1.154413762e-05 -1.130348608e-05 5.2e-15 13.53
21 2.6e-15 2.0e-08 2.9e-18 1.45e-01 -6.080209731e-06 -5.960160864e-06 7.0e-16 14.17
22 6.9e-16 3.2e-08 3.0e-19 1.33e-01 -2.801916059e-06 -2.721701236e-06 1.1e-16 15.31
23 5.9e-16 2.8e-07 1.8e-19 5.14e-01 -2.590845848e-06 -2.532166053e-06 7.1e-17 15.84
24 5.3e-16 7.8e-06 4.0e-20 3.26e-01 -1.420289373e-06 -1.385140295e-06 1.0e-17 16.38
25 6.4e-16 4.4e-06 5.0e-20 2.81e-01 -8.169523092e-07 -8.018784040e-07 1.3e-18 16.97
26 6.6e-16 3.1e-06 1.6e-21 -1.84e-01 -3.988525491e-07 -3.895729258e-07 2.1e-19 17.55
Optimizer terminated. Time: 17.59

Interior-point solution summary
Problem status : PRIMAL_AND_DUAL_FEASIBLE
Solution status : OPTIMAL
Primal. obj: -3.9885254919e-07 nrm: 1e-01 Viol. con: 1e-10 var: 0e+00 barvar: 0e+00 cones: 0e+00
Dual. obj: -3.8951429815e-07 nrm: 3e+05 Viol. con: 0e+00 var: 0e+00 barvar: 7e-10 cones: 0e+00
Optimizer summary
Optimizer - time: 17.59
Interior-point - iterations : 26 time: 17.55
Basis identification - time: 0.00
Primal - iterations : 0 time: 0.00
Dual - iterations : 0 time: 0.00
Clean primal - iterations : 0 time: 0.00
Clean dual - iterations : 0 time: 0.00
Simplex - time: 0.00
Primal simplex - iterations : 0 time: 0.00
Dual simplex - iterations : 0 time: 0.00
Mixed integer - relaxations: 0 time: 0.00

Status: Solved
Optimal value (cvx_optval): +3.89514e-07

Mark_L_Stone · May 10, 2021, 1:27pm

What happens if you leave cvx_precision at default? The Mosek people do not reconmend changing it from default.

1446324166 · May 10, 2021, 1:30pm

I leave cvx_precision at default,

covar = eye(size(H{1},1));
epsilon = 1e-3;

cvx_precision default %best % high? low ? medium
% cvx_solver mosek
cvx_begin sdp

variable Q(37,37) complex hermitian
variable U(37,37) complex hermitian
variable D_B(37,16) complex

% minimize( real(trace(Q * d * d’)) )
minimize( trace([real(Q * d * d’) imag(Q * d * d’);…
imag(Q * d * d’) real(Q * d * d’) ] ) )
[Q eye(37); …
eye(37) U ] >= 0;
[U D_B;… D_B’ H{1}’ * H{1} ] >= 0;
norm( covar.^0.5 *(D_B - H{1}), ‘fro’ ) <= sqrt(epsilon);
cvx_end

Here is the result:

Calling Mosek 9.1.9: 9471 variables, 3923 equality constraints
For improved efficiency, Mosek is solving the dual problem.

Problem
Name :
Objective sense : min
Type : CONIC (conic optimization problem)
Constraints : 3923
Cones : 1
Scalar variables : 1186
Matrix variables : 2
Integer variables : 0

Optimizer started.
Presolve started.
Linear dependency checker started.
Linear dependency checker terminated.
Eliminator started.
Freed constraints in eliminator : 0
Eliminator terminated.
Eliminator - tries : 1 time : 0.00
Lin. dep. - tries : 1 time : 0.02
Lin. dep. - number : 0
Presolve terminated. Time: 0.03
Problem
Name :
Objective sense : min
Type : CONIC (conic optimization problem)
Constraints : 3923
Cones : 1
Scalar variables : 1186
Matrix variables : 2
Integer variables : 0

Optimizer - threads : 4
Optimizer - solved problem : the primal
Optimizer - Constraints : 3922
Optimizer - Cones : 1
Optimizer - Scalar variables : 1185 conic : 1185
Optimizer - Semi-definite variables: 2 scalarized : 16697
Factor - setup time : 0.58 dense det. time : 0.00
Factor - ML order time : 0.16 GP order time : 0.00
Factor - nonzeros before factor : 6.07e+06 after factor : 6.07e+06
Factor - dense dim. : 2 flops : 1.17e+10
ITE PFEAS DFEAS GFEAS PRSTATUS POBJ DOBJ MU TIME
0 4.0e+00 1.0e+00 1.2e+01 0.00e+00 1.078091442e+01 0.000000000e+00 1.0e+00 0.64
1 8.5e-01 2.1e-01 4.1e+00 -8.53e-01 3.450716834e+00 -1.810695397e+00 2.1e-01 1.24
2 1.1e-01 2.7e-02 2.4e-01 1.11e-01 -9.303731649e-01 -1.733217328e+00 2.7e-02 1.81
3 6.3e-03 1.6e-03 3.4e-03 1.17e+00 -1.423387997e-01 -1.830590373e-01 1.6e-03 2.42
4 1.1e-03 2.7e-04 2.8e-04 8.68e-01 -5.537669385e-02 -6.188782836e-02 2.7e-04 2.92
5 1.7e-04 4.2e-05 2.2e-05 7.44e-01 -2.645045314e-02 -2.723537572e-02 4.2e-05 3.52
6 3.2e-05 8.1e-06 2.3e-06 5.51e-01 -1.756040827e-02 -1.770233324e-02 8.1e-06 4.08
7 5.3e-06 1.3e-06 2.8e-07 7.94e-02 -7.827966333e-03 -7.717110728e-03 1.3e-06 4.59
8 1.5e-06 3.8e-07 6.3e-08 5.05e-01 -4.997426540e-03 -4.888073631e-03 3.8e-07 5.11
9 5.2e-07 1.3e-07 1.7e-08 5.19e-01 -3.552141570e-03 -3.470225164e-03 1.3e-07 5.59
10 1.3e-07 3.1e-08 3.1e-09 4.39e-01 -2.219054936e-03 -2.165172129e-03 3.1e-08 6.11
11 2.9e-08 7.2e-09 5.0e-10 3.02e-01 -1.370240166e-03 -1.340397205e-03 7.2e-09 6.59
12 6.1e-09 1.5e-09 7.8e-11 2.23e-01 -7.889729774e-04 -7.724152117e-04 1.5e-09 7.11
13 1.4e-09 3.5e-10 1.3e-11 2.80e-01 -4.506254366e-04 -4.405945546e-04 3.4e-10 7.63
14 3.4e-10 1.5e-10 2.5e-12 3.36e-01 -2.718409410e-04 -2.658648290e-04 8.5e-11 8.14
15 7.5e-11 7.2e-11 4.1e-13 3.55e-01 -1.664255088e-04 -1.630508473e-04 1.9e-11 8.63
16 1.7e-11 4.6e-10 7.2e-14 2.62e-01 -1.010381683e-04 -9.901119761e-05 4.3e-12 9.14
17 3.9e-12 4.1e-10 1.3e-14 2.62e-01 -6.069352252e-05 -5.944296667e-05 9.6e-13 9.63
18 4.0e-13 8.3e-10 1.0e-15 2.75e-01 -3.240464962e-05 -3.173581567e-05 1.1e-13 10.86
19 5.7e-14 1.0e-08 1.1e-16 1.40e-01 -1.784600698e-05 -1.751477956e-05 1.6e-14 11.39
20 1.9e-14 6.1e-09 3.0e-17 1.35e-01 -1.154413762e-05 -1.130348608e-05 5.2e-15 11.88
21 2.6e-15 2.0e-08 2.9e-18 1.45e-01 -6.080209731e-06 -5.960160864e-06 7.0e-16 12.42
22 6.9e-16 3.2e-08 3.0e-19 1.33e-01 -2.801916059e-06 -2.721701236e-06 1.1e-16 13.39
23 5.9e-16 2.8e-07 1.8e-19 5.14e-01 -2.590845848e-06 -2.532166053e-06 7.1e-17 13.88
24 5.3e-16 7.8e-06 4.0e-20 3.26e-01 -1.420289373e-06 -1.385140295e-06 1.0e-17 14.42
25 6.4e-16 4.4e-06 5.0e-20 2.81e-01 -8.169523092e-07 -8.018784040e-07 1.3e-18 14.97
26 6.6e-16 3.1e-06 1.6e-21 -1.84e-01 -3.988525491e-07 -3.895729258e-07 2.1e-19 15.53
Optimizer terminated. Time: 15.59

Interior-point solution summary
Problem status : PRIMAL_AND_DUAL_FEASIBLE
Solution status : OPTIMAL
Primal. obj: -3.9885254919e-07 nrm: 1e-01 Viol. con: 1e-10 var: 0e+00 barvar: 0e+00 cones: 0e+00
Dual. obj: -3.8951429815e-07 nrm: 3e+05 Viol. con: 0e+00 var: 0e+00 barvar: 7e-10 cones: 0e+00
Optimizer summary
Optimizer - time: 15.59
Interior-point - iterations : 26 time: 15.53
Basis identification - time: 0.00
Primal - iterations : 0 time: 0.00
Dual - iterations : 0 time: 0.00
Clean primal - iterations : 0 time: 0.00
Clean dual - iterations : 0 time: 0.00
Simplex - time: 0.00
Primal simplex - iterations : 0 time: 0.00
Dual simplex - iterations : 0 time: 0.00
Mixed integer - relaxations: 0 time: 0.00

Status: Solved
Optimal value (cvx_optval): +3.89514e-07

Mark_L_Stone · May 10, 2021, 1:32pm

it looks like the problem was that Q and U weren’t hermitian, so you did not originally specify the SDP constraints you thought you did.

1446324166 · May 10, 2021, 1:38pm

The matrix Q and U should be hermitian, So I think I should add this initialization

variable Q(37,37) complex hermitian
variable U(37,37) complex hermitian

1446324166 · May 11, 2021, 8:58pm

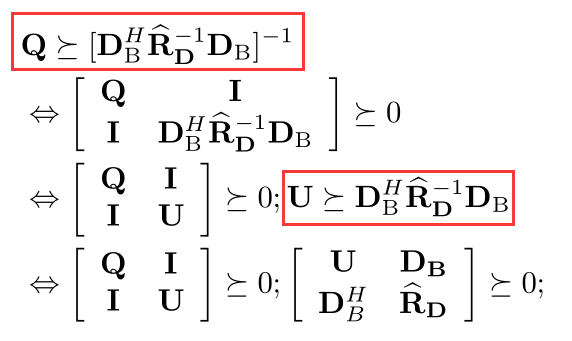
Dear Mark
Thanks for your reply, I have some questions on SDP.
My problem is solving a Inequality constrained optimization problem in Eq. (22)，including the matrix inversion in the Eq. (22). It seems that Eq. (22) is no longer convex. So I transfer the Eq. (22) to a SDP Eq. (26) using the Schur complement, the final solution obtained by the CVX is the exact solution or approximate solution of Eq. (22)? I am a little worry about the solution of Eq. (26) is far away from the Eq. (22).

Mark_L_Stone · May 11, 2021, 9:09pm

You have a bunch of stuff thrown all over the place. i don’t know what is supposed to go with what, and what the relationships among the symbols are… Perhaps you don’t either. i don’t know which of this stuff is manipulations in a book or paper vs. your own attempted transformations. I suggest you first make that clear to yourself.

Complex-value SDP， status: Inaccurate/Solved

Hello，there. Recently I met a complex-value SDP(See Fig1) and I have written an example, in order to fulfil the CVX requirement, I transform the complex cost function Q d_z d_z^H to the real from. Fig 1865×546 40 KB

% minimize( real(trace(Q * d * d’)) ) minimize( trace([real(Q * d * d’) imag(Q * d * d’);… imag(Q * d * d’) real(Q * d * d’) ] ) ) [Q eye(37); … eye(37) U ] >= 0; [U D_B;… D_B’ H{1}’ * H{1} ] >= 0; norm( covar.^0.5 *(D_B - H{1}), ‘fro’ ) <= sqrt(epsilon); cvx_end

Calling SDPT3 4.0: 9471 variables, 3923 equality constraints For improved efficiency, SDPT3 is solving the dual problem.

version predcorr gam expon scale_data HKM 1 0.000 1 0 it pstep dstep pinfeas dinfeas gap prim-obj dual-obj cputime

Thanks for your reply :grinning, I have try to use the Mosek like that, and get the result:Status: Infeasible.

% minimize( real(trace(Q * d * d’)) ) minimize( trace([real(Q * d * d’) imag(Q * d * d’);… imag(Q * d * d’) real(Q * d * d’) ] ) ) [Q eye(37); … eye(37) U ] >= 0; [U D_B;… D_B’ H{1}’ * H{1} ] >= 0; norm( covar.^0.5 *(D_B - H{1}), ‘fro’ ) <= sqrt(epsilon); cvx_end

Calling Mosek 9.1.9: 9471 variables, 3923 equality constraints For improved efficiency, Mosek is solving the dual problem.

Thanks for your suggestions, I have declared Q and U as complex hermitian, also I adjust the solver precision.

% minimize( real(trace(Q * d * d’)) ) minimize( trace([real(Q * d * d’) imag(Q * d * d’);… imag(Q * d * d’) real(Q * d * d’) ] ) ) [Q eye(37); … eye(37) U ] >= 0; [U D_B;… D_B’ H{1}’ * H{1} ] >= 0; norm( covar.^0.5 *(D_B - H{1}), ‘fro’ ) <= sqrt(epsilon); cvx_end

Calling Mosek 9.1.9: 9471 variables, 3923 equality constraints For improved efficiency, Mosek is solving the dual problem.

I leave cvx_precision at default,

% minimize( real(trace(Q * d * d’)) ) minimize( trace([real(Q * d * d’) imag(Q * d * d’);… imag(Q * d * d’) real(Q * d * d’) ] ) ) [Q eye(37); … eye(37) U ] >= 0; [U D_B;… D_B’ H{1}’ * H{1} ] >= 0; norm( covar.^0.5 *(D_B - H{1}), ‘fro’ ) <= sqrt(epsilon); cvx_end

Calling Mosek 9.1.9: 9471 variables, 3923 equality constraints For improved efficiency, Mosek is solving the dual problem.

Hello，there. Recently I met a complex-value SDP(See Fig1) and I have written an example, in order to fulfil the CVX requirement, I transform the complex cost function Q d_z d_z^H to the real from.

Fig 1865×546 40 KB

% minimize( real(trace(Q * d * d’)) )
minimize( trace([real(Q * d * d’) imag(Q * d * d’);…
imag(Q * d * d’) real(Q * d * d’) ] ) )
[Q eye(37); …
eye(37) U ] >= 0;
[U D_B;… D_B’ H{1}’ * H{1} ] >= 0;
norm( covar.^0.5 *(D_B - H{1}), ‘fro’ ) <= sqrt(epsilon);
cvx_end

Calling SDPT3 4.0: 9471 variables, 3923 equality constraints
For improved efficiency, SDPT3 is solving the dual problem.

version predcorr gam expon scale_data
HKM 1 0.000 1 0
it pstep dstep pinfeas dinfeas gap prim-obj dual-obj cputime

% minimize( real(trace(Q * d * d’)) )
minimize( trace([real(Q * d * d’) imag(Q * d * d’);…
imag(Q * d * d’) real(Q * d * d’) ] ) )
[Q eye(37); …
eye(37) U ] >= 0;
[U D_B;… D_B’ H{1}’ * H{1} ] >= 0;
norm( covar.^0.5 *(D_B - H{1}), ‘fro’ ) <= sqrt(epsilon);
cvx_end

Calling Mosek 9.1.9: 9471 variables, 3923 equality constraints
For improved efficiency, Mosek is solving the dual problem.

% minimize( real(trace(Q * d * d’)) )
minimize( trace([real(Q * d * d’) imag(Q * d * d’);…
imag(Q * d * d’) real(Q * d * d’) ] ) )
[Q eye(37); …
eye(37) U ] >= 0;
[U D_B;… D_B’ H{1}’ * H{1} ] >= 0;
norm( covar.^0.5 *(D_B - H{1}), ‘fro’ ) <= sqrt(epsilon);
cvx_end

Calling Mosek 9.1.9: 9471 variables, 3923 equality constraints
For improved efficiency, Mosek is solving the dual problem.

% minimize( real(trace(Q * d * d’)) )
minimize( trace([real(Q * d * d’) imag(Q * d * d’);…
imag(Q * d * d’) real(Q * d * d’) ] ) )
[Q eye(37); …
eye(37) U ] >= 0;
[U D_B;… D_B’ H{1}’ * H{1} ] >= 0;
norm( covar.^0.5 *(D_B - H{1}), ‘fro’ ) <= sqrt(epsilon);
cvx_end

Calling Mosek 9.1.9: 9471 variables, 3923 equality constraints
For improved efficiency, Mosek is solving the dual problem.