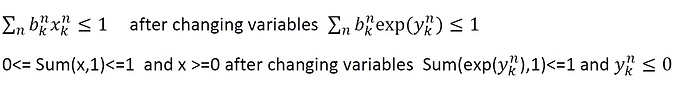I have an optimization problem that is not convex, by changing the variables (x=exp(y) and y=ln x, that y is the new variable), it changes to the convex problem.
In old problem my constraints were x>=0 and sum(x,1)<=1 , i.e., the elements of x and also the summation of column of x are between 0 and 1. Now, by this changing on the variables, I faced with Failed status that I think my constraints are its cause.
For x>=0, I have not considered equivalent constraint and for sum(x,1)<=1 the equivalent constraint (that I not sure is true) is sum(exp(y),1)<= exp(log(1))
For more detail, my code is attached. I will appreciate you if advise me.
my code:
close all;
clear;
clc;
M=3;%num_rrh
N=2;%num_channel
K=4;%num_user
n_harvest=2;
user_per_rrh=[4 4 4];
E0=.02;
mean_fading=1;
Nfade=100;
N0=10^-9;
Bw=100e6;
loc_r=[200 600 1000];
loc_bbu=[700 1200];
pathloss=1;
slot_num=10;
energy_threshold=6e-4;
% pmax_r=4;
% pr_max=pmax_r*ones(1,M);
min_user_rate=0;
n_l=2;
R_rrh_min=0;
landa=0.005;
p_threshold=1e-5;
a_threshold=1e-2;
dinke_ite=2;
info=[];
info_asm=[];
slot_duration=1;
max_itr=4;
alfa_asm=zeros(1,max_itr)
b_asm=[];
e_asm=[];
pr_asm=[];
din_threshold=1e-3;
pmax_r=1;
e_nkm_old=(1/N)*ones(N,K,M);
rrh_fad=rand(N,M);
user_fad= rand(N,K,M);
e_avail=ones(1,K,M);
pr_max=pmax_r*ones(1,M);
b_nkm_old=(1/N)*ones(N,K,M);
p_rrh_old=(pmax_r/2)*ones(N,M);
alfa_old=[.5 .5 .5];
b_nkm_old= ones(N,K,M);
y_nkm_old=exp(e_nkm_old);
cvx_begin
variables y_nkm(N,K,M) pr(N,M)
cnr=rrh_fad./(N0*Bw);
% tr=log(1+cnr.*pr);
tr = -rel_entr(ones(N,M),1+cnr.*pr);
r_rrh=cvx(zeros(N,M));
objfunc=cvx(zeros(K,M));
J_1=b_nkm_old.*(user_fad.^2);
for m=1:M
E_km=e_avail(:,:,m);
J_2=J_1(:,:,m);
for k=1:K
lj(m,k)=sum(J_2(:,k)*E_km(k),1);
end
end
[sj ij]=sort(lj,2,'descend');
for m=1:M
E_km=e_avail(:,:,m);
r_rrh(:,m)=((1-alfa_old(m))*tr(:,m));
x=cvx([]);
s_omeg=0;
makhraj_o=0;
for k=1:K
t=0;
sum_o=0;
ma2=0;
for n=1:N
t=t+1;%
x(t)=y_nkm(n,ij(m,k),m)+log(E_km(1,ij(m,k))*b_nkm_old(n,ij(m,k),m)*(user_fad(n,ij(m,k),m)^2))+log(N0*alfa_old(m));
s_omeg=s_omeg+exp(y_nkm_old(n,ij(m,k),m)+log(E_km(1,ij(m,k))*b_nkm_old(n,ij(m,k),m)*(user_fad(n,ij(m,k),m)^2))+log(N0*alfa_old(m)));%y+D+n0
sum_o=sum_o+exp(y_nkm_old(n,ij(m,k),m)+log(E_km(1,ij(m,k))*b_nkm_old(n,ij(m,k),m)*user_fad(n,ij(m,k),m)));
ma2=ma2+y_nkm_old(n,ij(m,k),m)+log(E_km(1,ij(m,k))*b_nkm_old(n,ij(m,k),m)*user_fad(n,ij(m,k),m));
makhraj_o=makhraj_o+y_nkm_old(n,ij(m,k),m)+log(E_km(1,ij(m,k))*b_nkm_old(n,ij(m,k),m)*(user_fad(n,ij(m,k),m)^2))+log(N0*alfa_old(m));
for nn=1:N
sum_o=sum_o+ exp(y_nkm_old(nn,ij(m,k),m)+ log(E_km(1,ij(m,k))*b_nkm_old(nn,ij(m,k),m)*user_fad(nn,ij(m,k),m)));
ma2=ma2+log(E_km(1,ij(m,k))*b_nkm_old(nn,ij(m,k),m)*user_fad(nn,ij(m,k),m));
end
for s=k+1:K%K-k:K
for n=1:N
t=t+1;
x(t)=y_nkm(n,ij(m,k),m)+log(E_km(1,ij(m,k))*b_nkm_old(n,ij(m,k),m)*user_fad(n,ij(m,k),m))+y_nkm(n,ij(m,s),m)+log(E_km(1,ij(m,s))*b_nkm_old(n,ij(m,s),m)*user_fad(n,ij(m,s),m));
s_omeg=s_omeg+exp(y_nkm_old(n,ij(m,k),m)+log(E_km(1,ij(m,k))*b_nkm_old(n,ij(m,k),m)*user_fad(n,ij(m,k),m))+y_nkm_old(n,ij(m,s),m)+log(E_km(1,ij(m,s))*b_nkm_old(n,ij(m,s),m)*user_fad(n,ij(m,s),m)));
makhraj_o=makhraj_o+y_nkm_old(n,ij(m,k),m)+log(E_km(1,ij(m,k))*b_nkm_old(n,ij(m,k),m)*user_fad(n,ij(m,k),m))+y_nkm_old(n,ij(m,s),m)+log(E_km(1,ij(m,s))*b_nkm_old(n,ij(m,s),m)*user_fad(n,ij(m,s),m));
end
end
say(m,ij(m,k))=-alfa_old(m)*log_sum_exp(x);
omega(m,ij(m,k))=-alfa_old(m)*log(sum_o+s_omeg);
for i=1:K
if(i~=ij(m,k))
s1=0;
for a=1:N
s1=s1+ exp(y_nkm_old(a,ij(m,k),m)+log(E_km(1,ij(m,k))*b_nkm_old(a,ij(m,k),m)*user_fad(a,ij(m,k),m))+y_nkm_old(a,ij(m,i),m)+log(E_km(1,ij(m,i))*b_nkm_old(a,ij(m,i),m)*user_fad(a,ij(m,i),m)));
end
gerad=(-alfa_old(m)*s1)/(ma2+makhraj_o);
else
s2=0;
s3=0;
for l=1:N
s2=s2+exp(y_nkm_old(l,ij(m,i),m)+log(E_km(1,ij(m,i))*b_nkm_old(l,ij(m,i),m)*(user_fad(l,ij(m,i),m)^2))+log(N0*alfa_old(m)));
s3=s3+exp(y_nkm_old(l,ij(m,i),m)+log(E_km(1,ij(m,i))*b_nkm_old(l,ij(m,i),m)*user_fad(l,ij(m,i),m)));
for r=1:N
s3=s3+exp(y_nkm_old(r,ij(m,i),m)+log(E_km(1,ij(m,i))*b_nkm_old(r,ij(m,i),m)*user_fad(r,ij(m,i),m)));
end
end
gerad=(-alfa_old(m)*(s2+s3))/(ma2+makhraj_o);
omega_hat(m,ij(m,k))=omega(m,ij(m,k))+(gerad*(y_nkm(n,ij(m,k),m)-y_nkm_old(n,ij(m,k),m)));
objfunc(m,ij(m,k))=say(m,ij(m,k))-omega_hat(m,ij(m,k));
end
end
end
end
end
maximize sum(sum(objfunc))+sum(sum(r_rrh))-(landa*sum(sum(pr)))
subject to
%constraint for the power of the rrh
for m=1:M
% temp=sum(pr,1);
% temp(:,m)-pr_max(m) <=0;
s=0;
for n=1:N
s=s+ pr(n,m);
end
s-pr_max(m) <=0;
end
%constraint for the enegy of the user
be=exp(log(b_nkm_old).*y_nkm);%b_nkm_old.*(exp(y_nkm));
for m=1:M
be_temp= be(:,:,m);
be_t2=sum(be_temp,1);
for k=1:K
be_t2(:,k)-1<=0;
end
end
for m=1:M
for n=1:N
pr(n,m)>=0;
end
end
y0=exp(y_nkm);
for m=1:M
y1=y0(:,:,m);
for k=1:K
sum(y1(:,k),1)-exp(log(1))<=0
end
end
cvx_end
y_nkm(N,K,M); pr(N,M);
v=exp(y_nkm);