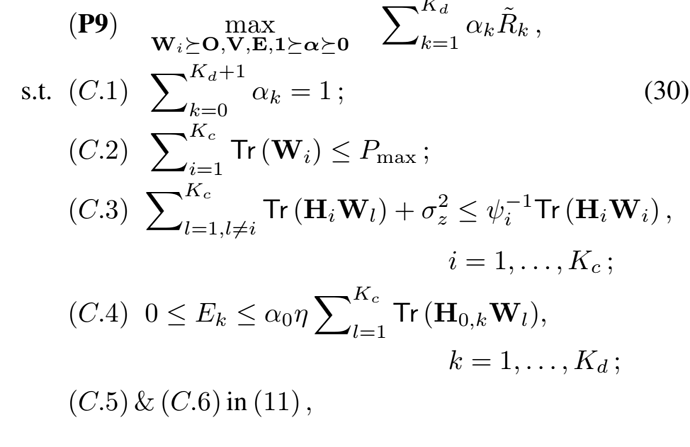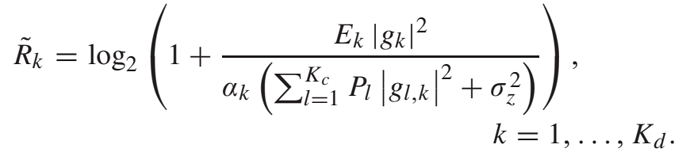Cannot perform the operation: {real affine} ./ {real affine} error on cvx matlab

1

Hi. i am trying to write this code on matlab with cvx.

cvx_p9
cvx_p9.png974×631 37.2 KB

V is a UL beamforming matrix that omit from problem and we find it with ZF beamforming.

W_i is a DL beamforming vector on sdp form

E and alpha are energy and time allocation

R_tilde(k) on objective function is concave on E(k) because logarithmic function is concave as you know.

rate_du
rate_du.png870×197 11.4 KB

alpha(k)*R_tilde(k) is a perspective function and it is concave on alpha and E also.

C.1 constraint is affine and C.2 to C.5 is convex and we find alpha_0 with exhaustive search from zero to one.

C.5 constraint is a linear constraint of alpha

this is the code that i wrote:

for aa=1:length(alpha0)
    cvx_begin 
               variable W_1(M(mm),M(mm)) complex hermitian semidefinite;
                variable W_2(M(mm),M(mm)) complex hermitian semidefinite;
                variable E1 nonnegative
                variable alpha1 nonnegative
                variable alpha2 nonnegative 
                maximize alpha1*log2(1 + (E1*(abs(g_du))^2)/(alpha1*(P_cu_1*(abs(g_cu_du(1)))^2 + P_cu_2*(abs(g_cu_du(2)))^2 + sigma2_w)))
                subject to
                    alpha0(aa) + alpha1 + alpha2 == 1;
                    real((trace(W_1) + trace(W_2))) <= P_w_max;
                    real((trace(H_cu_1*W_2) + sigma2_w)) <= real(trace(H_cu_1*W_1))/saai_w(ii);
                                    real((trace(H_cu_2*W_1) + sigma2_w)) <= real(trace(H_cu_2*W_2))/saai_w(ii);
                    0 <= E1 <= alpha0*eta*real((trace(H_0(:,1:7)*W_1) + trace(H_0(:,1:7)*W_2)));
                                    f_MU(alpha1,Z,P_cu_1,h_cu(:,1)) + f_MU(alpha2,Z,P_cu_1,h_cu(:,1)) - zeta(zz) <= 0;
                   f_MU(alpha1,Z,P_cu_2,h_cu(:,2)) + f_MU(alpha1,Z,P_cu_2,h_cu(:,2)) - zeta(zz) <= 0;
             cvx_end
             R_tilde_hybrid_ex(aa)= cvx_optval;
end

on the objective function line in matlab, it gives me this error:
Cannot perform the operation: {real affine} ./ {real affine}
i don’t know what the problem is. please help me.

2

The problem is that you are not following CVX’s rules.

That said, the objective function can be formulated using rel_entr so that CVX will accept it.

Use the fact that
alpha_k*log(1+y/alpha_k) = -rel_entr(alpha_k,alpha_k+y)
The correct y to use is easily determined, but I don’t feel like writing out that mess.

1 Like
3

It works now. thank you very much.

about this mention i don’t understand what you really mean. if you mean that my code is not very good i will rewrite & make it more clean after i debug.