Cannot perform the operation: {real affine} .* {convex}

1

Hi.I writting my optimization problem in cvx and running that but i had a error .And I think the error is in the following part of the optimization problem:
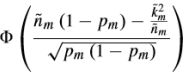
image
where m,p are constants and m=3. k(3,1) and n(3,1) are the variables.
How can I express it in a DCP-compliant manner?
normcdf(((sqrt(n(m))(1-p(m))-k(m)inv_pos(sqrt(n(m)))))/sqrt(p(m)(1-p(m))), 0, 1)
What’s wrong in the expression given above?I get the error that"Disciplined convex programming error:
Cannot perform the operation: {real affine} . {convex}"
please if it is possible help me…

2

You are not following the DCP rules.

I think you can handle an approximation of the log of \Phi as a concave function of k and n (I don’t understand exactly how you are dealing with the vector aspect of k and n, so I 'll leave those details to you).

Use quad_over_lin for k^2/n, which will result in a concave argument of \Phi. Then use log_norm_cdf for the log of \Phi. If you need \Phi instead of log(\Phi), you are out of luck.

help log_normcdf

log_normcdf Logarithm of the cumulative normal distribution.
Y = log_normcdf(X) is the logarithm of the CDF of the normal
distribution at the point X.

                             1    / x
    log_normcdf(X) = LOG( ------- |   exp(-t^2/2) dt )
                          sqrt(2) / -Inf

For numeric X, log_normcdf(X) is computed using the equivalent 
expression LOG(0.5*ERFC(-X*SQRT(0.5))). When X is a CVX variable, a 
a piecewise quadratic *approximation* is employed instead. This
approximation gives good results when -4 <= x <= 4, and will be
improved in future releases of CVX.

For array values of X, the log_normcdf returns an array of identical
size with the calculation applied independently to each element.

X must be real.

Disciplined convex programming information:
    log_normcdf is concave and nondecreasing in X. Therefore, when used
    in CVX specifications, X must be concave.
3

Oh thank you so much.The quad_over_lin and log_normcdf is very helpful to me,and this optimization problem can be solved by cvx if there is image .But sir,if I use image here,is this problem not solved by cvx?

4

If you can’t use log(\Phi), then you can not handle it in CVX.

If \Phi is an objective function to be maximized, then you can maximize log(\Phi) instead. If you have a constraint \Phi \ge constant, you can change that to log(\Phi) \ge log(constant).

5

OK I got it.I will replace image with image in this optimization problem.Thank you so much,sir.