Hello, after seeing the topics related to my problem, I couldn’t solve it. So my code is:
clear; clf;
A=[1 0 0.1 0; 0 1 0 0.1; 0 0 0.9 0; 0 0 0 0.9];
B=[0 0; 0 0; 0.1 0; 0 0.1];
E=[1 0 0 0; 0 1 0 0]; % 2x4
T=80;
p_inicial=[0; 5];
p_final= [15; -15];
U_max=15;
e= power(10,-6);
M=10;
w=[10 20 30 30 20 10; 10 10 10 0 0 -10]; %Waypoints
wt=[10 25 30 40 50 60] +1; %Index begin at 1
for m=0
cvx_begin quiet
variable x(4,T+1);
variable u(2,T);
expression f(6);
for k=1:1:6
f(k)= inv_pos (norm( E* pow_p(x(:,wt(k)) , 2) - w(:,k) ) ) * norm(E*x(:,wt(k))-w(:,k),2);
end
minimize(sum(f(1:6)));
subject to
x(:,1)==[p_inicial; 0; 0]
x(:,T+1)==[p_final; 0; 0]
for i=1:1:T
norm(u(:,i),2)<=U_max;
x(:,i+1)== A*x(:,i)+B*u(:,i);
end
cvx_end
where the objective function that i’m trying to implement is:
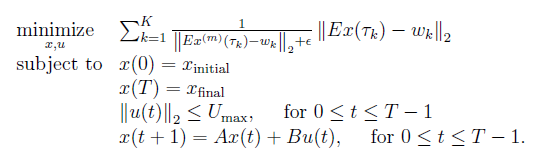
I have the following error:
Error using cvx/norm (line 52)
Disciplined convex programming error:
Cannot perform the operation norm( {convex}, 2 )
Is there a way of doing the power of x inside a norm? or is there other solution for this problem?
Thank you all.
Best regards.