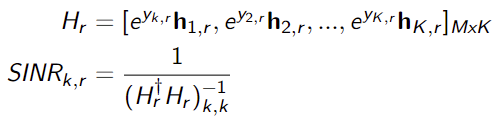Cannot perform the operation: {log-affine} .* {complex affine}

Nonconvex
1

clc
clear
close all;

%% Initialization of parameters & channel setup
K=5;%Number of users
Nru=2;%Number of RUs
N_pkts=randi([1 5],K,1);
w=N_pkts;
Tsls=zeros(K,1);

global ap_ant;
ap_ant=8;
M=ap_ant;
Nrx=8;

Pt_dB=30;%uplink transmit power in dBm
Pt=10^(Pt_dB/10);

%Path-loss at d0
d0=1;%in meters
c=3e8;%in m/s
fc=5e9;%in Hz
lambda=c/fc;
PL0=(lambda/(4pid0))^2;
PL0_dB=10*log10(PL0);

a=3.8;%pathloss exponent
dmax=20;%in meters
PL=zeros(1,K);
PL_dB=zeros(1,K);
d=zeros(1,K);
for k=1:K
d(k)=randi([2,dmax]);%user distance in meters
PL(k)=PL0*(d0/d(k))^a;
PL_dB(k)=10*log10(PL(k));%pathloss in dB
end

Kc=1.380649E-23;
T=290;%in kelvin;B=160e6;%MHz
N_sc=106;%Number of subcarriers in an RU
B_sc=78.125e3;%Subcarrier bandwidth
B_ru=N_scB_sc;
sigma2=KcTB_ru;
sigma2dB=10log10(sigma2*1e3);%%noise power in dBm

%channel matrix
%Y=zeros(Nru,K,K);N=zeros(Nru,K,K);n=zeros(K,Nru);
G=zeros(Nru,K,K);

%Generation of channel matrix
H=zeros(Nru,Nrx,K);
for r=1:Nru
for k=1:K
H(r,:,k)=(sqrt((PL(k))/2)).(randn(Nrx,1)+1irandn(Nrx,1));
end
end
% H=abs(H);
%% cvx solver
cvx_begin
cvx_solver mosek
variable y(K,Nru);
C2=[];
C3=[];
for r=1:Nru
for k=1:K
Hr=reshape(H(r,:,:),Nrx,K);
Xr=reshape(exp(y(1:K,r)),1,K);
XH=repmat(Xr,Nrx,1);
Heq=XH.*Hr;
Hi=real(inv(Heq’Heq));
SINR(k,r)=1/(sigma2(Hi(k,k)));
R(k,r)=log(1+SINR(k,r));
end
C3=[C3 sum(exp(y(k,:)))];
end
for r=1:Nru
C2=[C2;sum(exp(y(:,r)))];
end
maximize(sum(R(k,r)),“all”);
subject to
exp(y(:,:))<= ones(K,Nru);
C2<=M.*ones(Nru,1);
C3<=1.*ones(1,K);
cvx_end
exp(y)

I have verified the objective function and the constraints are convex and
I see the below error message.
Error using .*
Disciplined convex programming error:
Cannot perform the operation: {log-affine} .* {complex affine}

Error in zf_cvx_resource_allocation (line 70)
Heq=XH.*Hr;

Please help to find out if this is accepted in CVX?
If this is not accepted format, can you please suggest any other format to solve this?

2

Leaving aside variable shapes, on a per element basis, Xr is basically exp(y), which is log-affine. and it is multiplied by Hr, which is a complex number. CVX can’t determine the curvature of that, so produces the error message. The next statement, involving, inv would also be disallowed. If this problem is convex (you claim to have proved that), I think you’ll need to apply something like Hr'*Hr in parentheses so that CVX never sees the complex number, rather than first multiplying by XH and then doing thing'*thing. I’ll let you work out the details. And then do you need HI with the inv, then taking the reciprocal of that for SINR`? Anyhow, your program is rather a mess, and I don’t have the energy to sort through whether it is actually convex, so I’ll let you sort through that.

3

Thanks very much, Mark for the reply and pointing out the mistakes.
Can you please suggest a way to implement the below equations in cvx in a better way?
cvx
Here, each h is a complex vector with size Mx1.

Also, how can I implement inverse in cvx?
I was unable to find a way to calculate a particular element of an inverse in CVX.

4

There is no general matrix inverse function in CVX, because that is neither convex nor concave. However, certain expressions involving matrix inverse can be formed, such as matrix_frac, which I mentioned in my previous post.

Apparently, you did not understand the link I provided. Your first step is to prove the optimization problem is convex. I don’t know that your problem is convex.

5

Thanks Mark for the details.

I did the following to verify that my objective function is convex.
I found the eigenvalues of the hessian matrix, and they turned out to be strictly positive.

But I did not use cvx DCP ruleset to prove the function is convex.
I will try this before trying to optimize the function.

6

Dud you prove the objective function’s Hessian has positive eigenvalues for A:LL values of the optimization variables. It would suffice for convexity for that to hold for all feasible values of the variables, but that is likely insufficient for a DCP formulation. And the constraints need to be convex as well.

If I had a nickel for every false claim of convexity on this forum, I wouldn’t be rich, but I would have quite a few dollars.

7

Thanks, Mark for your valuable time.
Yes, I had tried the simulation for 1e5 times and did not find any negative eigenvalue.
Also, the hessian matrix here is diagonal and I found it had only positive entries for all the 1e5 trials.

I could not find the close form of the hessian for this objective function.
So I tried the above process to convince the objective is convex.
But I understand this is insufficient for a DCP formulation and use cvx for this problem.

Can you please suggest any other tool or a way to solve this optimization problem?
Even in MATLAB’s inbuilt optim solver, I could not use complex numbers.

8

You can try YALMIP. If the problem really is convex and the solver converges to optimality, it should find the global optimum, rather than a non-globally optimal stationary point, even if a non-convex solver is used.

9

Thanks Mark for the great suggestion. I’m able to implement matrix inverse in yalmip using one of your another suggestion: matrices - Finding a matrix to force a part of another matrix to be with null trace - Mathematics Stack Exchange

However, I’m not able to find the global optimum using fmincon as the solver. Solvers like mosek, gurobi and bmibnb are not supported for either equality constraints or multi-variable monomial equality constraints.

I tried using cplex version 12.10 as a solver with yalmip. But cplex does not support polynomial equality constraints. Do you have any suggestion on solvers to be used with yalmip for this problem?

Below is the modified matlab code for yalmip. I apologize if this is not a right forum to ask about yalmip.

%% yalmip solver
y=sdpvar(K,Nru,'full');
Hi_inverse=sdpvar(Nru,K,K,'full','complex');
Hi=sdpvar(Nru,K,K,'full','complex');
C2=[];
C3=[];
for r=1:Nru
    Hr=reshape(H(r,:,:),Nrx,K);
    Xr=reshape(exp(y(1:K,r)),1,K);
    Hi(r,:,:)=((Hr'*Hr).*(Xr'*Xr));
    for k=1:K
        SINR(k,r)=1/(sigma2*(Hi_inverse(r,k,k)));
        R(k,r)=log2(1+SINR(k,r));
    end    
end
for k=1:K
    C3=[C3 sum(exp(y(k,:)))];
end
for r=1:Nru
    C2=[C2;sum(exp(y(:,r)))];
end
Objective=sum(R(k,r),"all");
Constraints=[exp(y(:,:))<= ones(K,Nru),exp(y(:,:))>= zeros(K,Nru),C2<=M.*ones(Nru,1),C3<=1.*ones(1,K)];
for r=1:Nru
    A=reshape(Hi(r,:,:),K,K);
    B=reshape(Hi_inverse(r,:,:),K,K);
    Constraints=[Constraints,A*B == eye(K,K)];
end
optimize(Constraints,-Objective,sdpsettings('solver','fmincon'));
10

In order fro H1_inverse to meaningfully be the inverse of H``, you need to include the constraint H1_Inverse*H1 == eye(K)` . I am leaving out the reshape mess, etc. which you need to deal with.

If FMINCON can’t find the global optimum, perhaps that’s because your problem is not convex. BMIBNB should be applicable, but whether it can succeed in a reasonable time depends on the problem.

For further YALMIP help, you should use an appropriate venue, such as https://groups.google.com/g/yalmip .

11

Thanks Mark for the quick response. Sorry if these questions are too basic to ask.
I’m getting the results are all NaN, while using BMIBNB. Is there a way to optimize the solver?

And while using fmincon, I see “Local minimum found that satisfies the constraints.” in MATLAB window.
Does it mean that the objective is non-convex?

12

As i wrote before, please use a YALMIP venue (there are two) for continued discussion of YALMIP implementation.

I see that Johan is now providing you help at the link provided. He certainly doesn’t think it’s a convex problem.