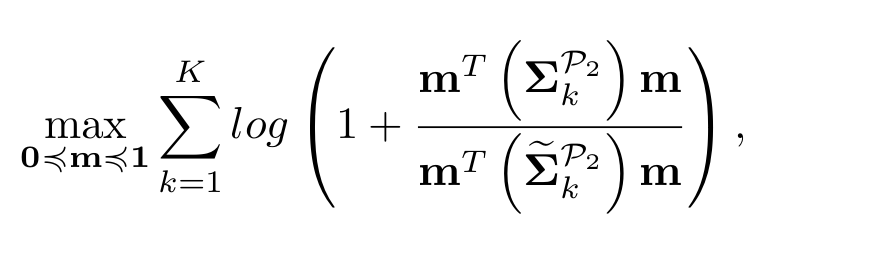I’m having difficulty solving the summation of logarithms. Can anyone offer suggestions or known solutions to address this issue? The vector m consists of components, each ranging between 0 and 1. Additionally, the terms sigma_k are real matrices and known to us.
The “difficulty” has nothing to do with the summation. Even when K = 1, the expression is neither concave nor convex. And I am giving the benefit of the doubt that the matrices are positive definite. If they have some special properties or relations beyond that, it is your fault for neglecting to tell us.
Consider the example with K=1 and the numerator matrix being diag([1 1]), and denominator matrix being diag([1 2]); The Hessian evaluated at m = [0.5;0.5] has one negative eigenvalue and one positive eigenvalue. So the expression is neither convex nor concave.
If the matrices are allowed to be PSD and not necessarily positive definite, the matrices diag([1 0]), diag([0 1]) results in different variables appearing in the numerator and denominator, log(1+m(1)^2/m(2)^2), making the indefiniteness even more apparent.
Thank you, Mark for your prompt analysis. My apologies, the sigma matrices are positive semi-definite and not necessarily positive definite. As you mentioned, the positive semi-definiteness of the matrices renders the expression indefinite. Are there any other viable solutions for this issue? Could we solve it by approximating the above function or using a non-convex solver?
You can try a non-convex solver under YALMIP.
Thank you Mark, I will try.