Can you help me with problems

1

My code

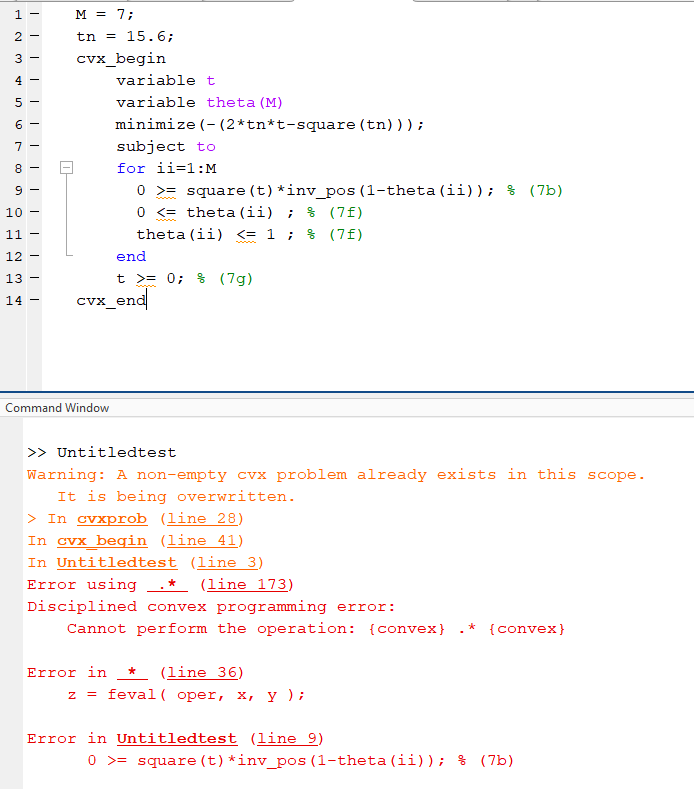
M = 7;
tn = 15.6;
cvx_begin
variable t
variable theta(M)
minimize(-(2tnt-square(tn)));
subject to
for ii=1:M
0 >= square(t)*inv_pos(1-theta(ii)); % (7b)
0 <= theta(ii) ; % (7f)
theta(ii) <= 1 ; % (7f)
end
t >= 0; % (7g)
cvx_end

12
12694×789 24.4 KB

2

When i run this code. It have a problems which i don’t know how to fix. Help me solve problems, please.

3

0 >= quad_over_lin(t,1-theta(ii))

help quad_over_lin

quad_over_lin Sum of squares over linear.
Z=quad_over_lin(X,Y), where X is a vector and Y is a scalar, is equal to
SUM(ABS(X).^2)./Y if Y is positive, and +Inf otherwise. Y must be real.

If X is a matrix, quad_over_lin(X,Y) is a row vector containing the values
of quad_over_lin applied to each column. If X is an N-D array, the operation
is applied to the first non-singleton dimension of X.

quad_over_lin(X,Y,DIM) takes the sum along the dimension DIM of X.
A special value of DIM == 0 is accepted here, which is automatically
replaced with DIM == NDIMS(X) + 1. This has the effect of eliminating
the sum; thus quad_over_lin( X, Y, NDIMS(X) + 1 ) = ABS( X ).^2 ./ Y.

In all cases, Y must be compatible in the same sense as ./ with the squared
sum; that is, Y must be a scalar or the same size as SUM(ABS(X).^2,DIM).

Disciplined convex programming information:
    quad_over_lin is convex, nonmontonic in X, and nonincreasing in Y.
    Thus when used with CVX expressions, X must be convex (or affine)
    and Y must be concave (or affine).

I suggest you carefully read the entire CVX Users’ Guide, where quad_over_lin and many other functions and language features are documented.