Can this SINR problem be solved by CVX?

[MatthewSin]

Hi. I am currently reforming a research paper related to SINR and power distribution problems.
The researchers said that this problem can be implemented in CVX. I want to reform it using CVXPY, but I am a beginner at CVX or CVXPY. Can somebody tell me whether CVX can solve this so I can implement it in CVXPY?

Article title: Multi-UAV Deployment for Throughput Maximization in the Presence of Co-Channel Interference
Article link: Multi-UAV Deployment for Throughput Maximization in the Presence of Co-Channel Interference | IEEE Journals & Magazine | IEEE Xplore

[Mark_L_Stone]

it looks straightforward in CVX or CVXPY, if you use log_sum_exp in the first constraint.

Mosek would be the preferred solver for this in CVX due to the exponential term.

[MatthewSin]

Thank you so much! It helps me a lot.

[Loco_Citato]

Hello MatthewSin, sorry to bother but I have a question which is similar to your work. I am now doing a cell-communication based proragmme which also requires the SCA/first-order Taylor expansion to convert my nonconvex formula into approximately convex form. (And it is based on this Paper) .

However, from the comman window, my feasible programme only gets “feasible” results, as shown below. It means that no matter how big the max bound for the feasible problem codes set, the programme will only give me the maxmim value based on what I set. I wonder if you met the same problem and how do you solve it? I am really looking forward to your reply.

[MatthewSin]

Hi everyone. I have encountered problem {log-convex} >= {log-concave} when dealing with constraints (24b). I have tried to reformulate the problem several times but still cannot solve it. Do there have any tricks for solving this type of problem?

My CVX code:
cvx_begin gp
variable z(1,n)
variable v(1,n)
variable y(1,n)
variable psi_z

maximize( psi_z )
subject to
for i = 1:size(Ku_cover)
for j = 1:size(UAV)
if j ~= Ku_cover(i,3) % exclude mth UAV
v(j) + power(norm(UAV(j,1:2)-Ku_cover(i,1:2)),2) + sigma >= exp(-y(j)); % (24b)
v(j)+power(z_appr(j),2) <= 2*z_appr(j)*z(j); % (24c)
end
end
end
cvx_end

The power() term and sigma are constants.

[Mark_L_Stone]

Why are you using gp mode? Are there any multiplications or divisions of CVX variables? is z_appr input data? I don’t see why that error message would correspond to this program (maaybe it has something to do with gp mode). Perhaps you’re not showing us everything? The program as it is doesn’t make any sense, because the variable psi_z is unconstrained, hence the problem is unbounded presuming it is feasible.

Whatever your problem is actually supposed to be, have you proven it is a convex optimization problem?

[MatthewSin]

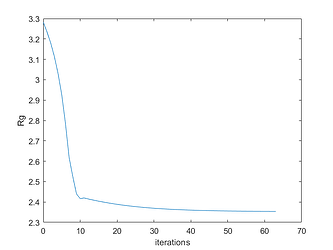
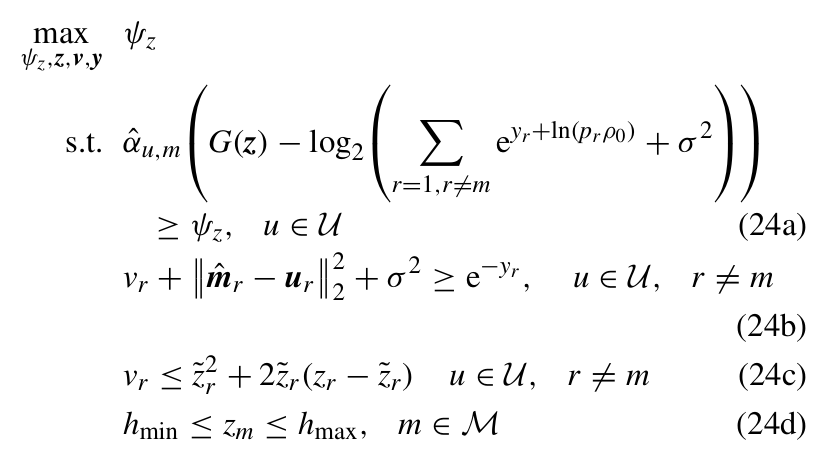Hi, Mr. Stone and everyone. I still need help with the same question. Actually, I am solving an alternating optimization problem. However, I might have programmed this question incorrectly because my result is weird. The graph below is my result, which shows the achievable rate by inputting parameter (i.e., z, p) after each iteration, which I denoted as “Rg.”

When doing each optimization independently, the Rg increases and converges after serval iterations, but alternative optimization is different. I am unsure if the problem was due to my worse coding or related to the alternative optimization.

The objective value is an affine function so that I can maximize this problem, and the following should be enough to determine the convexity.

Altitude:

maximize (objective affine variable)
s.t.
-a*sum(z^2) - log_sum_exp(y) + C >= objective (constraint 24a)
affine >= affine or convex (constraints 24b,c,d)

Power:

maximize (objective affine variable)
s.t.
log(x)-(b*sum(p) + C) >= objective (constraint 30a)
C <= z <=C (constraint 30b)

I believe 24a is valid because a is always a positive constant in -a*sum(z^2), which is convex, and log_sum_exp(y) is also convex, so -(a*z^2 + log_sum_exp(y)) is concave. Also, as x is always positive in 30a, the log(x) is concave. Therefore, I believe CVX can solve my problems.

The following is my full code and input data:

cvx_solver mosek
cvx_save_prefs
% problem constants
load('matlab_matrix_ideal_small.mat');

n = size(UAV,1);           % number of transmitters and receivers

Pmin = 0.1*ones(1,n);      % minimum power
Pmax = 1*ones(1,n);        % maximum power
hmin = 50*ones(1,n);       % minimum altitude
hmax = 200*ones(1,n);      % maximum altitude
sigma = 10^(-120/10);      % noise power % -90 or -100
rho = 10^(-30/10);

p = 0.5*ones(1,n);
z = 100*ones(1,n);
p_appr = p; % initial point
z_appr = z; % initial point

prio = 0; 
% 0 == z frist -> p second 
% 1 == p first -> z second

% no_iter = 4;
% no_tot_iter = 12;
max_iter = 100;
% For the convenient, we will use Ku_cover => [x, y, mth_UAV] 

% comparsion and break
prev_psi_z = 0;
prev_psi_p = 0;
prev_Rg = 0;
epsilon = 1e-4;

% variables are power levels
tot_iter = 1;
result = [];
fin = 0; % when each iteration finished, fin = 2

disp("======================"+tot_iter+"========================")
while(1)
%% ========================== Altitude ====================================
    if prio == 0 && fin ~= 2
        disp("altitude loop...")
        iter = 1;
        prev_psi_z = 0;
        
        while(1)
            if iter > 1
                z_appr = z;
            end
            %disp("altitude iteration: "+ iter);

            w_st = [];
            w_nd = [];
            for u = 1:size(Ku_cover)
                GT = Ku_cover(u, 1:2);
                m = Ku_cover(u, 3)+1;

                temp_w_st = [];
                temp_w_nd = [];
                for r = 1:size(UAV)
                    mUAV = UAV(r, 1:2);

                    temp_w_st = [temp_w_st -(p(r)*rho)/(power((power(z_appr(r),2)+power(norm(mUAV-GT),2)),2)*log(2))];
                    temp_w_nd = [temp_w_nd (p(r)*rho)/(power(z_appr(r),2)+power(norm(mUAV-GT),2))];
                end
                w_nd = cat(2, w_nd, (sum(temp_w_nd)+sigma)); % w_nd(u)
                w_st = cat(3, w_st, temp_w_st); % w_st(:,r,u)
            end
            G_st = log(w_nd)/log(2); % G_st(u)

            cvx_begin quiet
                cvx_precision default
                variable psi_z
                variable z(1,n)
                variable v(1,n)
                variable y(1,n)

                log_sum_exp_y = [];
                for m = 1:size(UAV)
                    seq = [];
                    for r = 1:size(UAV)
                        if r ~= m
                            seq = [seq r]; % without m_th
                        end
                    end

                    log_sum_exp_y = cat(2, log_sum_exp_y, log(sum(exp(y(seq)+log(p(seq)*rho)))+sigma)/log(2) ); % log_sum_exp_y(m)
                end

                pow_z = power(z,2); % pow_z(m)

                Ru = [];
                for u = 1:size(Ku_cover)
                    m = Ku_cover(u,3)+1;
                    Ru = cat(2,Ru, G_st(u) + (w_st(:,:,u)/w_nd(u))*transpose(pow_z-power(z_appr,2)) - log_sum_exp_y(m) );
                end

                maximize psi_z
                subject to
                    Ru >= psi_z;

                    for u = 1:size(Ku_cover)
                        GT = Ku_cover(u, 1:2);
                        m = Ku_cover(u, 3)+1;

                        for r = 1:size(UAV)
                            mUAV = UAV(r, 1:2);
                            if r ~= m
                                v(r) + power(norm(mUAV-GT),2) >= exp(-y(r));
                            end
                        end
                    end

                    for r = 1:size(UAV)
                        v(r) <= power(z_appr(r),2) + 2*z_appr(r)*(z(r)-z_appr(r));
                    end

                    hmin <= z <= hmax;
            cvx_end

            disp("optimal altitude: "); disp(psi_z);
            % disp("objective improvement: "+ (psi_z-prev_psi_z));
            if (abs(psi_z-prev_psi_z) < epsilon)
                z_appr = z; % last update
                break
            else
                prev_psi_z = psi_z;
                if iter == max_iter
                    z_appr = z; % last update
                    break
                end 
            end
            iter = iter+1;
        end
        
        prio = 1; % switch to power optimization
        fin = fin + 1; % Finish 1 optimization
    end
    
%% =========================== Power ================================
    if prio == 1 && fin ~= 2
        disp("power loop...")
        temp = 0;
        iter = 1;
        prev_psi_p = 0;

        while(1)    
            %disp("power iteration: "+ iter);
            if iter > 1
                p_appr = p;
            end

            w_st = [];
            w_nd = [];
            for u = 1:size(Ku_cover)
                GT = Ku_cover(u, 1:2);
                m = Ku_cover(u,3)+1;

                temp_w_st = [];
                temp_w_nd = [];
                for r = 1:size(UAV)
                    mUAV = UAV(r, 1:2);

                    if r ~= m
                        temp_w_st = [temp_w_st (rho/(power(z(r), 2) + power(norm(GT-mUAV),2)))/log(2)];
                        temp_w_nd = [temp_w_nd (p_appr(r)*rho)/(power(z(r), 2) + power(norm(GT-mUAV),2))];
                    else
                        temp_w_st = [temp_w_st 0];
                    end
                end
                w_st = cat(3, w_st, temp_w_st); % w_st(:,r,u)
                w_nd = cat(2, w_nd, sum(temp_w_nd)+sigma ); % w_nd(u)
            end
            Q_st = log(w_nd)/log(2); % Q_st(u)


            cvx_begin quiet
               cvx_precision default
               variable psi_p
               variable p(1,n)

               Ru = [];
               for u = 1:size(Ku_cover)
                   GT = Ku_cover(u, 1:2);
                   m = Ku_cover(u, 3)+1;

                   h = [];
                   seq = [];
                   for r = 1:size(UAV)
                       mUAV = UAV(r, 1:2);
                       h = [h rho/(power(z(r), 2) + power(norm(GT-mUAV),2))]; % h(r)

                       if r ~= m 
                           seq = [seq r]; % without m_th
                       end
                   end
                   Ru = cat(2, Ru, log(p*transpose(h)+sigma)/log(2)-( Q_st(u) + (w_st(:,seq,u)/w_nd(u))*transpose(p(seq)-p_appr(seq))) );
               end

               maximize psi_p
               subject to
                    Ru >= psi_p;
                    Pmin <= p <= Pmax;
            cvx_end

            disp("optimal power: "); disp(psi_p);
            % disp("objective improvement: "+ (psi_p-prev_psi_p));

            if (abs(psi_p-prev_psi_p) < epsilon)
                p_appr = p; % last update
                break
            else
                prev_psi_p = psi_p;   
                if iter == max_iter
                    p_appr = p; % last update
                    break
                end 
            end

            iter = iter+1;
        end 
        
        prio = 0;
        fin = fin + 1;
    end
    
%% ========================== Result Comparsion ============================= %
    % comparison when finish both optimization
    if fin == 2
        Rg = [];
        for u = 1:size(Ku_cover)
            m = Ku_cover(u,3)+1;
            GT = Ku_cover(u,1:2);

            I = [];
            for r = 1:size(UAV)
                mUAV = UAV(r,1:2);
                if r ~= m
                    % Interference
                    I = [I p(r)*rho/(power(z(r),2)+power(norm(mUAV-GT),2))];
                end
            end
            sum_I = sum(I);

            mUAV = UAV(m, 1:2);
            S = p(m)*rho/(power(z(m),2)+power(norm(mUAV-GT),2));
            N = sigma;

            temp_Rg = log(1+S/(sum_I+N))/log(2);
            Rg = [Rg temp_Rg];
        end

        disp("min: "+ min(Rg) + "<after> <-> " + min(prev_Rg)+"<before>");
        fprintf('\n'); disp("objective improvement: (<" + epsilon+")");
        disp("altitude: "+ (psi_z-prev_psi_z));
        disp("power: "+ (psi_p-prev_psi_p));
        disp("Minimum ach. rate: "+(min(Rg)-min(prev_Rg)));
        result = [result min(Rg)];
        if (abs(min(Rg)-min(prev_Rg)) < epsilon)
            break
        else
            prev_Rg = Rg;
            if (tot_iter == max_iter)
                break
            end
            tot_iter = tot_iter + 1;
        end
        prev_psi_z = psi_z; prev_psi_p = psi_p; fprintf('\n\n')
        
        fin = 0; % reset fin, do next iteration
        disp("======================"+tot_iter+"========================")
    end
    
end

“matlab_matrix_ideal_small.mat” contains UAV = [x_coordinate, y_coordinate, radius] and Ku_cover = [x_coordinate, y_coordinate, m_th_UAV]

UAV = [661.3286  685.2581  101.7455; 99.0194  104.2281  101.7455; 709.5000   90.0000  101.7455; 143.0000  704.0000  101.7455]

Ku_cover = [714.0000  758.0000         0; 695.0000  602.0000         0; 730.0000  633.0000         0; 606.0000  756.0000         0; 602.0000  713.0000         0; 129.0000    7.0000    1.0000; 62.0000  199.0000    1.0000; 143.0000   50.0000    1.0000;  51.0000   76.0000    1.0000; 196.0000 135.0000    1.0000; 781.0000   29.0000    2.0000;  747.0000   77.0000    2.0000;  698.0000   20.0000    2.0000;  638.0000  151.0000    2.0000; 616.0000   76.0000    2.0000; 134.0000  772.0000    3.0000; 140.0000  728.0000    3.0000; 152.0000  636.0000    3.0000; 181.0000  664.0000    3.0000; 165.0000  666.0000    3.0000; 661.3286  685.2581         0; 99.0194  104.2281    1.0000; 709.5000   90.0000    2.0000; 143.0000  704.0000    3.0000]

I am sorry for asking this long question. I am really new to CVX and optimization problems.

[Mark_L_Stone]

You should be grateful if alternating optimization works well, not shocked if it doesn’t.

The result obtained using the SeDuMi solver is inaccurate. The optimal solution is not as good as before the optimization.

Unsafeguarded (no line search or trust region)Successive Convex Approximation (SCA) or generally, alternating variables optimization are unreliable. It might not descend (for minimization problem), i.e., iterates could get worse. It might not converge to anything; and if it does converge, it might not be to a local optimum of the original problem, let alone a global optimum. The solution of successive iterations, and therefore subproblem inputs, can become wilder and wilder, until at some point …