I want to find the optimized vectors w_r and w_t jointly in the following problem.
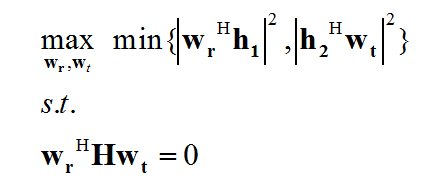
where H is a known matrix with M * N dimensions, h_2 is an N * 1 known vector and h_1 is an M * 1 known vector.
Also, w_t is an N * 1 vector and w_r is an M * 1 vector; (.)^H denotes the hermitian operator.
Can the above problem be solved using CVX?
If yes? how?
It is worth noting that I wrote the objective function of the above problem in MATLAB as follows and received an error message.
cvx_begin
variable wt(N) complex % N is known parameter
variable wr(M) complex % M is known parameter
maximize min ( square_pos ( norm((h_2’ * wt),1) ) , square_pos ( norm((wr’ * h_1),1) ) )
cvx_end
% command window message:
Disciplined convex programming error:
Cannot perform the operation min( {convex}, {convex} )
Thank you in advance for your helps and suggestions.