Can someone please help me with my SDP problem?

[Ciyuan]

My propose is to get two approximate Hermite matrices S and V, which represent the covariance matrix of two variables.
The problem is as follows:

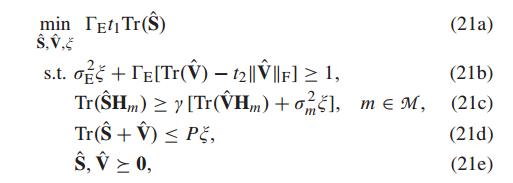
My code is as follows:

function [S,V,z]= solve_21(gamma,H)
    P = 100; 
    [Nt,~,M] = size(H);
    e = 0.1;
    GammaE = 1;
    alpha = log(e^(-1));
    t1 = 1 + alpha + sqrt(2*alpha); 
    t2 = sqrt(2*alpha);
  
cvx_begin SDP quiet
    variable neta
    variable S_bar(Nt,Nt)  hermitian semidefinite
    variable V_bar(Nt,Nt) hermitian semidefinite

minimize( GammaE*t1*trace(S_bar) );    
subject to 
    ( neta + GammaE * (trace(V_bar) - t2 * norm(V_bar,'fro')) ) >= 1;
    for m = 1:M
        trace(S_bar * H(:,:,m)) >=  gamma * ( trace(V_bar*H(:,:,m)) +  neta);
    end
    trace(S_bar + V_bar)  <= P*neta ;
    S_bar >= 0;
    V_bar >= 0;
    neta  >= 0;
 cvx_end

S = S_bar / neta;
V = V_bar / neta;
z = GammaE * t1 * trace(S_bar);

In my settings, all the sigmas are 1, so sigma is omitted in the code. The code below are used togenerate additional parameters.

clear all;
M = 3;
Nt = 4;
H = [];
for m = 1:M
    h(m,:) =1/sqrt(2*Nt)*( randn(1,Nt) + 1i* randn(1,Nt));
    H(:,:,m) =  h(m,:)'* h(m,:);
end

P = 10^(2);
e = 0.1;
sigma = 1;
sigma_e = 1;
GammaE = 1;

I have a problem that the result doesn’t satisfy the constraint of the inequality.

trace(S_bar * H(:,:,m)) - gamma * ( trace(V_bar*H(:,:,m)) +  neta)

ans =

   9.0576e-09 + 5.5511e-17i

It can not satisfy the constrain of (21c).

I know the reason could be relevant to solver tolerance, so I changed the constrain condition,such as :" ( neta + GammaE * (trace(V_bar) - t2 * norm(V_bar,‘fro’)) ) >= 1.01;" and " trace(S_bar + V_bar) <= P*neta + 0.1;"

But it still can’t work, the result is even “NaN”.

I found there is a constrain error is because the result z should be smaller than gamma, But after the CVX calculation, z is 500+ when gamma is 70+.
I want to know that

1. whether my code have something with it.
2. how can I solve the solver tolerance problem.
3. whether the question (22) is solvable.

Thank you !

[Mark_L_Stone]

The violation of the first constraint you discuss is just roundoff level error. In order to control this, you need to adjust the feasibility tolerance, not the optimality tolerance. Perhaps the default feasibility tolerance is 1e-8. Perhaps you can make it a little smaller, such as 1e-10, maybe 1e-12…

0.1 is too much to add. Add an amount a little larger than the feasibility tolerance. So at the default value of feasibility tolerance (perhaps 1e-8), perhaps add 1e-7. By adding 0.1, maybe you are making the problem infeasible.

In order to assess the results, you need to look at the solver or CVX output. If CVX claims the problem was not solved, or is infeasible, then all variable values are meaningless, and you cannot expect that constraints will be satisfied. So the number one thing you need to do is remove the quiet option. Then when you run the program, you will see the solver and CVX output. Or at least check cvx_status after CVX completes.

[Ciyuan]

Thanks for your replying!
I add " cvx_precision high" to my function and the result shows that the problem is solved……

Calling SDPT3 4.0: 87 variables, 34 equality constraints
   For improved efficiency, SDPT3 is solving the dual problem.
------------------------------------------------------------

 num. of constraints = 34
 dim. of sdp    var  = 32,   num. of sdp  blk  =  4
 dim. of socp   var  = 17,   num. of socp blk  =  1
 dim. of linear var  =  6
*******************************************************************
   SDPT3: Infeasible path-following algorithms
*******************************************************************
 version  predcorr  gam  expon  scale_data
   HKM      1      0.000   1        0    
it pstep dstep pinfeas dinfeas  gap      prim-obj      dual-obj    cputime
-------------------------------------------------------------------
 0|0.000|0.000|1.5e+02|2.3e+02|2.1e+04|-1.238978e+01  0.000000e+00| 0:0:00| chol  1  1 
 1|0.174|0.479|1.2e+02|1.2e+02|1.7e+04|-1.377289e+01 -3.680283e+02| 0:0:00| chol  1  1 
 2|1.000|0.664|8.8e-06|4.1e+01|3.8e+03|-2.122679e+01 -4.783623e+02| 0:0:00| chol  1  1 
 3|1.000|0.927|1.7e-05|3.0e+00|2.6e+02|-2.363549e+01 -3.790088e+01| 0:0:00| chol  1  1 
 4|1.000|0.290|2.8e-06|2.1e+00|2.5e+02|-2.212676e+02 -4.134203e+01| 0:0:00| chol  1  1 
 5|0.067|0.154|2.5e-06|1.8e+00|3.3e+02|-1.932409e+02 -1.796838e+02| 0:0:00| chol  1  1 
 6|0.212|0.619|1.9e-06|6.8e-01|2.5e+02|-3.278005e+02 -3.894243e+02| 0:0:00| chol  1  1 
 7|0.396|1.000|1.2e-06|2.7e-06|2.4e+02|-3.953272e+02 -6.397815e+02| 0:0:00| chol  1  1 
 8|0.866|1.000|1.6e-07|1.0e-06|6.7e+01|-4.796485e+02 -5.471154e+02| 0:0:00| chol  1  1 
 9|1.000|0.763|1.3e-08|4.7e-07|2.7e+01|-4.832654e+02 -5.102544e+02| 0:0:00| chol  1  1 
10|0.974|0.973|3.4e-10|8.6e-08|1.6e+00|-4.933835e+02 -4.950137e+02| 0:0:00| chol  1  1 
11|0.916|0.961|2.8e-11|2.4e-08|1.5e-01|-4.937971e+02 -4.939448e+02| 0:0:00| chol  1  1 
12|0.998|1.000|1.9e-12|6.6e-09|4.2e-02|-4.938303e+02 -4.938719e+02| 0:0:00| chol  1  1 
13|0.974|0.970|1.5e-12|2.0e-10|1.2e-03|-4.938374e+02 -4.938386e+02| 0:0:00| chol  1  1 
14|0.986|0.986|3.3e-12|3.8e-12|1.8e-05|-4.938375e+02 -4.938375e+02| 0:0:00| chol  1  1 
15|1.000|0.694|6.1e-11|2.2e-12|9.0e-06|-4.938375e+02 -4.938375e+02| 0:0:00| chol  1  1 
16|1.000|0.691|1.8e-11|2.2e-12|4.7e-06|-4.938375e+02 -4.938375e+02| 0:0:00| chol  1  1 
17|1.000|0.685|5.2e-12|2.9e-12|2.5e-06|-4.938375e+02 -4.938375e+02| 0:0:00| chol  1  1 
18|1.000|0.680|1.7e-12|2.0e-12|1.3e-06|-4.938375e+02 -4.938375e+02| 0:0:00| chol  1  1 
19|1.000|0.678|1.1e-12|1.6e-12|6.9e-07|-4.938375e+02 -4.938375e+02| 0:0:00| chol  1  1 
20|1.000|0.675|2.6e-12|1.5e-12|3.7e-07|-4.938375e+02 -4.938375e+02| 0:0:00| chol  1  1 
21|1.000|0.670|1.6e-12|1.5e-12|2.0e-07|-4.938375e+02 -4.938375e+02| 0:0:00| chol  1  1 
22|1.000|0.663|6.3e-12|1.5e-12|1.1e-07|-4.938375e+02 -4.938375e+02| 0:0:00| chol  1  1 
23|1.000|0.652|2.1e-10|1.8e-12|5.9e-08|-4.938375e+02 -4.938375e+02| 0:0:00| chol  2  1 
24|1.000|0.634|1.5e-10|2.5e-12|3.4e-08|-4.938375e+02 -4.938375e+02| 0:0:00| chol  2  1 
25|1.000|0.610|7.3e-10|3.8e-12|2.1e-08|-4.938375e+02 -4.938375e+02| 0:0:00|
  stop: relative gap < infeasibility
  lack of progress in infeas
-------------------------------------------------------------------
 number of iterations   = 25
 primal objective value = -4.93837504e+02
 dual   objective value = -4.93837504e+02
 gap := trace(XZ)       = 1.06e-07
 relative gap           = 1.07e-10
 actual relative gap    = 1.07e-10
 rel. primal infeas (scaled problem)   = 6.31e-12
 rel. dual     "        "       "      = 1.51e-12
 rel. primal infeas (unscaled problem) = 0.00e+00
 rel. dual     "        "       "      = 0.00e+00
 norm(X), norm(y), norm(Z) = 1.6e+03, 7.6e+01, 9.7e+01
 norm(A), norm(b), norm(C) = 2.0e+02, 1.2e+01, 1.5e+00
 Total CPU time (secs)  = 0.37  
 CPU time per iteration = 0.01  
 termination code       = -1
 DIMACS: 1.2e-11  0.0e+00  1.5e-12  0.0e+00  1.1e-10  1.1e-10
-------------------------------------------------------------------

------------------------------------------------------------
Status: Inaccurate/Solved
Optimal value (cvx_optval): +493.838

But I calculated the constrain (17) by

 " ( neta + GammaE * (trace(V_bar) - t2 * norm(V_bar,'fro')) )-1"

and the result it returns is 8.8785e-12.
Two similar results were given under the two different tolerance settings. Does it means that the CVX return the right answer actually? And there is something wrong with the optimal question?

[Erling (Erling D.Andersen)]

To me it seems is that you get almost the precision out of SDTP3 that possible.

Recall that computations are done in finite precision so you will never get an 100% accurate solutions.
I assume you are aware of that.

Believing you can get an absolute accuracy of less 1.0e-12 in absolute sense is a bit naive. Sorry.

There are SDP optimizers that can compute solutions with high accuracy but they are likely to be awfully slow.