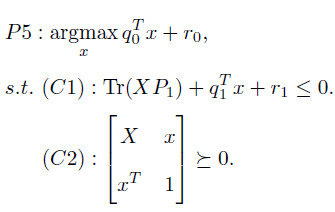I got an optimization problem, as shown like this
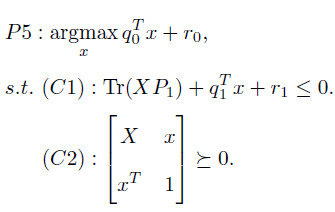
The variable is x, and the matrix X=xx^T. I am really confused on how to programme the constraint (C2).
For example, I assume that the variable x is a three-elements vector and specify it as
variable x(3)
and then specify the matrix X=xx^T. The objective is quite linear, and the constraint (C1) is also easy to build. But I got no idea on the second constraint (C2), how to program it? Can someone help me on this? Thanks very much for your kind help.
1 Like
This is addressed in the CVX Users’ Guide http://cvxr.com/cvx/doc/sdp.html .
[X x;x' 1] == semidefinite(4)
or if using SDP mode
[X x;x' 1] >= 0
Note that you have not modeled X = x*x’ . Constraint C2 is a semidefinite relaxation of that.
Note that I have removed the TFOCS designation from the thread. If you really want to solve this problem using TFOCS rather than CVX, please say so.
1 Like
Hi Mark, really thanks for your kind help! I tried to program it in Matlab like this
q=[1,2,3];
cvx_begin sdp
variable x(3)
X=xx’; % matrix X
minimize 1+qx
subject to
[X x;x’ 1] == semidefinite(4); % constraint (C2)
cvx_end
Unfortunately, a waring " Only scalar quadratic forms can be specified in CVX" always returned. Is there any mistake when I define matrix X? Thanks for your kind reply.
1 Like
You are not “supposed to” use X= x*x’. Constraint C2 is a semidefinite relaxation of it, and that is what you should enter. You will have to determine whether this is the model you want. Alternatively, if X is input data rather than an optimization (CVX) variable, you need to remove the declaration of X(3,3) as being a variable.
P1 = randn(3,3); P1 = P1*P1'; % I made up some data
r1 = 0; % I made up some data
q = [1,2,3];
cvx_begin
variables X(3,3) x(3,1)
minimize 1+ q*x
subject to
trace(X*P1) + q*x + r1 <= 0
[X x;x' 1] == semidefinite(4); % constraint (C2)
cvx_end
which produced
Calling SDPT3 4.0: 11 variables, 2 equality constraints
------------------------------------------------------------
num. of constraints = 2
dim. of sdp var = 4, num. of sdp blk = 1
dim. of linear var = 1
*******************************************************************
SDPT3: Infeasible path-following algorithms
*******************************************************************
version predcorr gam expon scale_data
HKM 1 0.000 1 0
it pstep dstep pinfeas dinfeas gap prim-obj dual-obj cputime
-------------------------------------------------------------------
0|0.000|0.000|1.3e+02|1.3e+01|1.0e+03| 0.000000e+00 0.000000e+00| 0:0:00| chol 1 1
1|0.864|0.996|1.7e+01|1.1e-01|9.1e+01|-3.949596e+00 -1.895868e+01| 0:0:00| chol 1 1
2|1.000|1.000|9.2e-08|6.1e-03|6.1e+00|-3.872070e+00 -9.961497e+00| 0:0:00| chol 1 1
3|0.910|1.000|2.2e-08|6.1e-04|1.4e+00|-5.739227e+00 -7.176243e+00| 0:0:00| chol 1 1
4|1.000|1.000|6.1e-09|6.1e-05|3.0e-01|-6.293679e+00 -6.591130e+00| 0:0:00| chol 1 1
5|0.975|0.983|2.5e-10|7.1e-06|6.6e-03|-6.458643e+00 -6.465075e+00| 0:0:00| chol 1 1
6|0.964|0.984|1.2e-11|7.2e-07|2.9e-04|-6.462935e+00 -6.463211e+00| 0:0:00| chol 1 1
7|1.000|1.000|1.0e-10|2.4e-12|2.4e-05|-6.463152e+00 -6.463177e+00| 0:0:00| chol 1 1
8|0.964|0.984|1.5e-10|3.7e-12|8.1e-07|-6.463171e+00 -6.463172e+00| 0:0:00| chol 1 1
9|1.000|1.000|6.8e-10|5.5e-12|1.6e-07|-6.463172e+00 -6.463172e+00| 0:0:00|
stop: max(relative gap, infeasibilities) < 1.49e-08
-------------------------------------------------------------------
number of iterations = 9
primal objective value = -6.46317150e+00
dual objective value = -6.46317166e+00
gap := trace(XZ) = 1.61e-07
relative gap = 1.16e-08
actual relative gap = 1.15e-08
rel. primal infeas (scaled problem) = 6.84e-10
rel. dual " " " = 5.49e-12
rel. primal infeas (unscaled problem) = 0.00e+00
rel. dual " " " = 0.00e+00
norm(X), norm(y), norm(Z) = 1.2e+01, 6.5e+00, 2.3e+01
norm(A), norm(b), norm(C) = 2.3e+01, 2.0e+00, 3.6e+00
Total CPU time (secs) = 0.45
CPU time per iteration = 0.05
termination code = 0
DIMACS: 6.8e-10 0.0e+00 8.0e-12 0.0e+00 1.1e-08 1.2e-08
-------------------------------------------------------------------
------------------------------------------------------------
Status: Solved
Optimal value (cvx_optval): -5.46317
Of course, the solution obtained depends on the random value of P which was generated.
Alternatively,
cvx_begin sdp
variables X(3,3) x(3,1)
minimize 1 + q*x
subject to
trace(X*P1) + q*x + r1 <= 0
[X x;x' 1] >= 0; % constraint (C2)
cvx_end
which produces the same result.
2 Likes
Amazing! It works now.
Really thanks for your kind help!