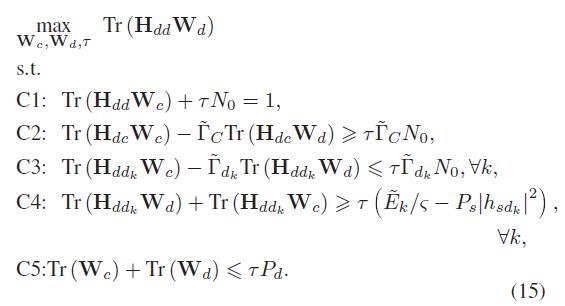
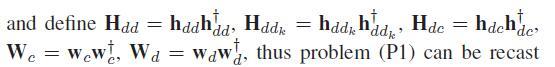
Can I use CVX to solve the problem which use function trace?I am sorry that my English is poor and any suggestion will be helpful for me!
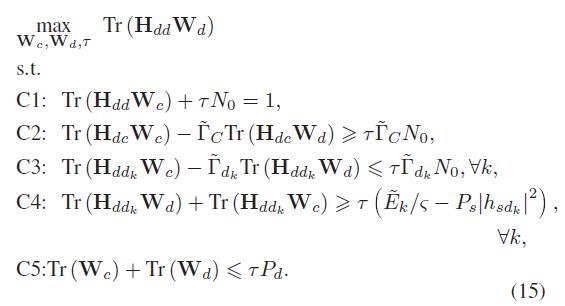
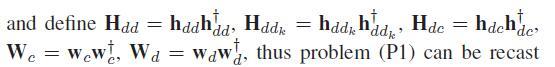
Can I use CVX to solve the problem which use function trace?I am sorry that my English is poor and any suggestion will be helpful for me!
Presuming that all variables other than the optimization variables W_c, W_d, and tau are inputs to the problem, and are not defined in terms of the optimization variables. this looks like a Linear Programming problem to me, which is easy to enter into CVX.
Presuming all these other variables already have numerical values, you should be able to enter this problem into CVX as written. Merely declare W_c, W_d, and tau as CVX variables of the appropriate type and dimensions. Then use maximize and trace, and == for equality constraint. You can use use a for loop over k for C3 and C4.
Ok! Get it!Thanks for your suggestion and I will have a try.
variable Wc(N,N)
variable Wd(N,N)
variable tao
This is the code that I wrote:
maximize trace(Hdd*Wd)
subject to
trace(Hdd*Wc)+tao*N0==1
trace(Hdc*Wc)-gammac1(j)*trace(Hdc*Wd)>=tao*gammac1(j)*N0
-trace(Hddk1*Wc)+gammadk1*trace(Hddk1*Wd)>=-tao*gammadk1*N0
trace(Hddk1*Wd)+trace(Hddk1*Wc)>=tao*(Ek/sigma-Ps*(abs(hsdk1))^2)
-trace(Wc)-trace(Wd)>=-tao*Pd
cvx_end
But errors occur as following:
wrong use cvxprob/newobj (line 43):
Expressions in objective functions must be real.
error in maximize (line 21):
newobj( prob, ‘maximize’, x );
error in D2D_ad (line 64):
maximize trace(Hdd*Wd)
Your objective function must evaluate to a real scalar. You haven’t shown us what Hdd is, but based on the error message, it must be complex.
I don’t know what your optimization problem is supposed to be. maximize(real(trace(Hdd*Wd))) or maximize(trace(real(Hdd*Wd))) would be acceptable to CVX, but I have no idea if that’s what you really want. You need to determine whether Wc and Wd need to be declared complex.
I’ll let you worry about whether you need a for loop over k to incorporate C3 and C4. As it is, your code presumes k = 1. CVX won’t complain about that, but it’s a question of whether you have entered your problem correctly (fully).
Also note this from The DCP ruleset — CVX Users' Guide
One or both sides of an equality constraint may be complex; inequality constraints, on the other hand, must be real. A complex equality constraint is equivalent to two real equality constraints, one for the real part and one for the imaginary part. An equality constraint with a real side and a complex side has the effect of constraining the imaginary part of the complex side to be zero.
Oh no!This is definition of the variables:
The channel coefficients of the S-CU, the S-DU and the SDUk (k ∈ {1, …,K}) links are denoted by the complex scalar hsc, hsd and hsdk , respectively. The N×1 complex channel vectors of the S-DT, DT-CU, DT-DU and DT-DUk links are represented by g, hdc, hdd and hddk , respectively.
Is that mean I can’t solve my problem with CVX:cry:
In order to make the problem easy to solve,I let k=1.
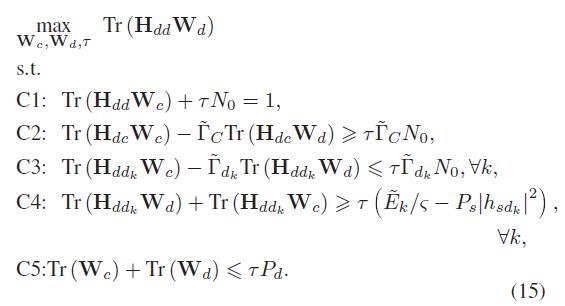
And I also don’t understand the objecttive and constraints in my problem.That is because I know the fact that a complex can’t be compared.
Now I find the mistakes that make objective function complex.And add some keywords to denote the objective function and constraints are not complex.But new problem occurs:
Status: Infeasible
Optimal value (cvx_optval): -Inf
How can I deal with it?
I know that there is a time difference between us and I will wait for your help.This is very important for me and many thanks for you!
cvx_begin
variable Wc(N,N) hermitian semidefinite
variable Wd(N,N) hermitian semidefinite
variable tau nonnegative
maximize trace(Hdd*Wd)
subject to
trace(Hdd*Wc)+tau*N0==1
trace(Hdc*Wc)-gammac1*trace(Hdc*Wd)>=tau*gammac1*N0
-trace(Hddk1*Wc)+gammadk1*trace(Hddk1*Wd)>=-tau*gammadk1*N0
trace(Hddk1*Wd)+trace(Hddk1*Wc)>=tau*(Ek/sigma-Ps*(abs(hsdk1))^2)
trace(Wc)+trace(Wc)<=tau*Pd
cvx_endO.k., you seem to be making progress. You haven’t provided the input data, so we can’t determine why it’s infeasible.
I can think of two possibilities. Either your problem is truly infeasible, or there is a roundoff level imaginary component in your constraints which is not small enough in magnitude to satisfy solver tolerance.
In the former case, taking the real part might allow the problem to be solved. So use real(left-hand side).
In the latter case, you can try deleting one or more constraints (maybe also with using real(left-hand side))… Or start with one constraint and add constraints until you find a constraint which is preventing feasibility. For diagnostic purposes, you can replace your objective with a least norm objective to minimize the infeasibility of one or more constraints (and remove those constraints). You could even combine all infeasibilities into one objective to be minimized and find out how close to zero it comes out.
Thanks! I will have a try as what you say.

Wc and Wd, N dimensions hermitian semidefinite matrix,are variables to be solved. Hdd and Hddk are N dimensions constants.others are scalar constant.
Is this question(Especially the constraints C2) convex?Can I deal with it by CVX? Why it occurred the following error when I run my code?
Disciplined convex programming error:
Cannot perform the operation: {real affine} ./ {real affine}
I need help and many thanks!
You haven’t told us what your CVX variables are. I am guessing zeta is a CVX variable, even though you don’t list it as being an optimization variable. If so, and it must be positive, use inv_pos(zeta), which is convex. Presuming the other term on the right-hand side of C2 is constant, C2 will be a convex function <= affine function, which is a convex constraint and should be accepted by CVX.
If my guess is incorrect, you would need to show us your CVX code.
Oh no ! In my topic made a mistake in’Especially the constraints C2’ .the right one is Especially the constraints C1 Sorry!
“Since problem (P4) is convex, it can be solved by CVX tools.”
NO, NO. I don’t know who wrote that, but it is logically incorrect. CVX does not claim to solve any problem that can be proved to be convex; see the FAQ for more details.
haha! I have to admit that this paper do have many priblems like this.