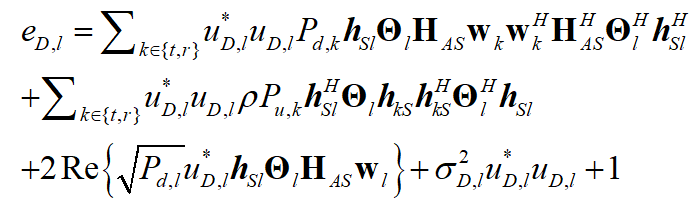For example, a is the variable vector of function f. Can i find its extreme values with help of cvx? Can I transform derivative into a maxmize vector a of object function f.
If f is concave, and all constraints, if any, are convex, you can use CVX to solve it, provided you can follow CVX’s rules.
Yes,It is convex of f,but log function can’t be sovled by cvx. How should i apprixmate this log into tractable form?

I have no idea what your optimization problem is.
if the only term in the objective function is log(convex), it is equivalent to i.e., you can instead use convex for the objective function, i.e., do not take log.This should work presuming you are minimizing the objective (subject to convex constrains which can be formulated in CVX).
excuse me,I have some difficulties in cvx,while I have found you are good at it. Can I ask you for help?
Thanks a lot. My objective function of the optimization problem is f with no constraints, cause this vector a is a random vector.
oh,sorry for that, i try to make it more understandable cause function expression is redundant.
Here’s the expression.
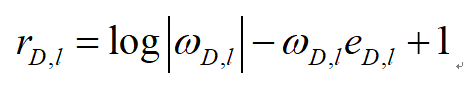
where u is the variable with dimesion number 2. The optimal value of omega is the inverse of e.
And we are going to abtain the first order derivative of u in function r.
I don’t see where r_{D,I} appears ion the expression. I also don’t know what is input data vs. optimization variables.
Nevertheless, it is your responsibility to prove that it is it convex (if you are minimizing).
I appreciate your answer, Mr.Stone. Have a nice day!