Can CVX accommodate the following concave expression?

1

Hello, CVX-savvy people. I’ll only share the relevant details from the successive convex approximation implementation by first-order Taylor expansion. Here is the initial non-convex optimization problem with a particular focus on constraint (21b):

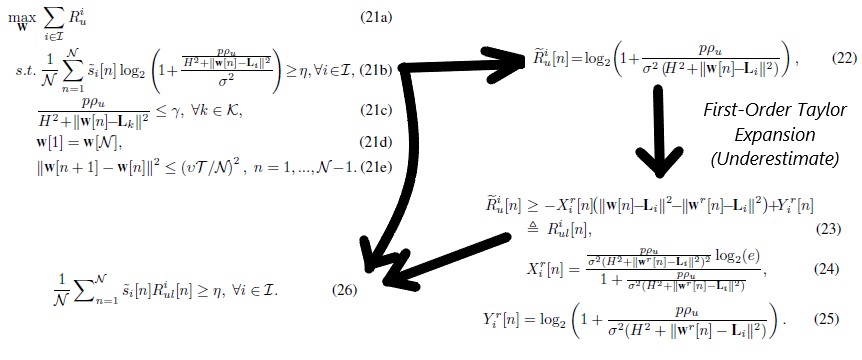
Illustration
Illustration862×360 54.3 KB

When I declare and assign an expression representing R_ul above, I’m warned that the DCP ruleset does not allow the {negative constant} * {convex} operation, even though the expression is sure to be concave, and nothing points as to such in the reference guide. This would probably be a silly mistake on my part, so I apologize in advance.

Thank you.

2

You haven’t shown the code, including variable declarations, and corresponding error message.

Of course, when using SCA, something which would have been a variable in the non-convex problem becomes input data, thereby resulting in a convex problem, and skirting DCP rules.

3

Thank you for the response, Mark, and sorry for not providing the code; it’s just a direct translation of the problem. Here goes:

cvx_begin
    variable W(N,2);
    **expression R_Ul_i(N,I);**
    expression I_U_k(N,K);
    expression trjlim(N-1,1);
    for n = 1:N
        for i = 1:I
            **X_i = p*rho/(noisvar*log(2))*inv_pos(square(H^2+norm(W_r(n,:)-L_U(i,:))))*inv_pos(1+p*rho/(noisvar*(H^2+norm(W_r(n,:)-L_U(i,:)))));**
            **Y_i = log(1+p*rho/noisvar*inv_pos(H^2+norm(W_r(n,:)-L_U(i,:))))/log(2);**
            **R_Ul_i(n,i) = -X_i*(norm(W(n,:)-L_U(i,:))-norm(W_r(n,:)-L_U(i,:)))+Y_i;**  
        end
        for k = 1:K
            I_U_k(n,k) = H^2+norm(W_r(n,:)-L_BS(k,:))+2*(W_r(n,:)-L_BS(k,:))*(W(n,:)-W_r(n,:)).';
        end
        if (n < N)
            trjlim(n) = norm(W(n+1)-W(n));
        end
    end
    **R_U_i_2 = 1/N*sum(s.*R_Ul_i);**
    R_sum_2 = sum(R_U_i_2);
    maximize( R_sum_2 );
    **subject to**
        **R_U_i_2 >= eta;**
        I_U_k >= p*rho/gamma;
        W(1,:) == W(N,:);
        trjlim <= (v*T/N)^2;
cvx_end

Note: The parts between double asterisks in the code are the one in question. Also, inputs {N,I,K,H,v,eta,T,p,rho,gamma,L_BS,L_U} are all predefined paramters, {s} is obtained by solving a previous optimization subproblem, and {W_r} is clearly the previous iteration result for the decision variable {W}.

Consequent error message:

Disciplined convex programming error:
    Cannot perform the operation: {negative constant}
    .* {convex}

Error in  *  (line 36)
    z = feval( oper, x, y );

Error in Alg_1 (line 52)
                R_Ul_i(n,i) =
                -X_i*(norm(W(n,:)-L_U(i,:))-norm(W_r(n,:)-L_U(i,:)))+Y_i;
4

The “legality” or not of various parts of your program depend on the numerical values of the input data, which you have not provided.

Suggestion: Just prior to where an error occurs, enter the expression in question, by itself, with no assignment or constraint. CVX will display what type of expression that is. As necessary, do this for pieces of the expression, until you see something which wouldn’t be what it needs to be.

1 Like
5

I think u are trouble in communication,or UAV communication,you may get some problem ,of course,the Taylor expansion is concave when x is greater than 0,I found some problem in your code ,|| x-q||^2 dont equal to norm,which equal to norm^2,but you cannot write it as norm^2 ,bacause it is illegal,you d better use the function sum_square,type help sum_square in command window will help you!

1 Like
6

Thank you, Chujain, for notcing the squared norms; I’d missed that for some reason.

Thank you, Mark, for your suggestion on checking the nature of the expressions, which I’ve applied to the code and found that R_Ul_i was a mixed convex/concave due to my incorrect usage of inv_pos for a constant expression (silly me!) causing a division by 0 in some elements. I fixed that and the values were neat and concavity was achieved.

The problem is now feasible and the results make sense. Much appreciated!

7

You can also use square_pos(norm(...)) for norm(...)^2