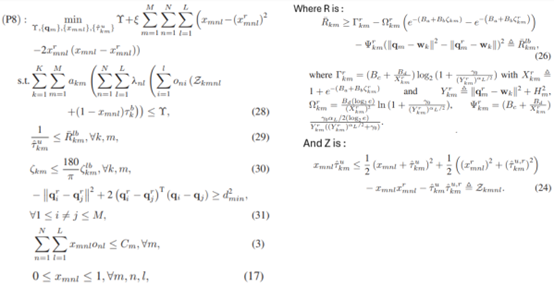Can anyone help with Scaling issue(maybe

[Allenyang (淙珺 楊)]

I’m trying to solve this convex problem,

The parameters’ description, I’m sorry it’s so long…

γ
This is the primary objective term or cost function component being minimized. It represents a specific performance metric, such as the total delay or system cost.

ξ
A positive weight or penalty coefficient used to balance the influence of the caching deviation term. It ensures that the caching optimization is properly weighted relative to other objectives.

xₘₙₗ
A decision variable representing the caching strategy, where xₘₙₗ ∈ [0,1].
It indicates the fraction of video layer l of video n cached on UAV m.

xₘₙₗʳ
The reference point for the caching variable xₘₙₗ in the Sequential Convex Approximation (SCA) method.
It is used to linearize the non-convex caching objective into a convex form.

τₖₘᵘ
A slack variable representing the transmission delay between user k and UAV m.
It is subject to the lower bound constraint based on the rate R̃ₖₘˡᵇ.

qₘ
A 2D or 3D vector representing the position of UAV m.
This variable is optimized for deployment purposes while ensuring safety constraints.

qᵣᵢ
The reference point for UAV i’s position in the SCA method.
It is used to linearize the non-convex safety distance constraint between UAVs.

aₖₘ
A binary association indicator that determines whether user k is associated with UAV m (1 if associated, 0 otherwise).

λₙₗ
The request probability for layer l of video n.
It reflects the demand of video content layers.

oₙᵢ
The size (in bits) of layer i of video n.
It is used to calculate the caching and transmission cost.

Zₖₘₙₗ
A term that aggregates the caching cost and delay components for user k, UAV m, video n, and layer l.

ζₖₘ
The elevation angle between UAV m and user k, expressed in degrees.

ζₖₘˡᵇ
The lower bound for the elevation angle ζₖₘ, ensuring sufficient line-of-sight (LoS) communication quality.

dₘᵢₙ²
The minimum squared safety distance that must be maintained between any two UAVs i and j to avoid collisions.

Code I wrote and debugged for 6 weeks

for iter = 1:max_iter
    disp(iter)
    epsilon = 1e-7; % Used to avoid division by zero
    total_sum = 0;
    % K is User , M is Uav , N M is for cache data
    % Solve the convex optimization problem for P8
    cvx_begin  
        variables R q_new(M, 2) x_new(M, N, L) tau_u(K, M) zeta_new(K, M)

        % Compute the summation part of the objective function
        C = 0;
        for m = 1:M
            for n = 1:N
                for l = 1:L
                    C = C + x_new(m, n, l) - x_ref(m, n, l)^2 ...
                        - 2 * x_ref(m, n, l) * (x_new(m, n, l) - x_ref(m, n, l));
                end
            end
        end
        
        % Final objective function
        minimize(R + xi * C) % R is the slack variable
        
        subject to

        % Constraint (30): Maximum elevation angle constraint
        for k = 1:K
            for m = 1:M
                norm_ref = norm(q_ref(m, :) - params.w_k(k, :));
                q_norm = norm(q_new(m, :) - params.w_k(k, :));
                zeta_new(k, m) <= (180/pi()) * (atan(uav_heights(m) / norm_ref) - ...
                              (uav_heights(m) / (norm_ref^2 + uav_heights(m)^2)) * ...
                              (q_norm - norm_ref));
            end
        end

        % Constraint (31): Safety distance constraint
        for i = 1:M-1
            for j = i+1:M
                -norm(q_ref(i, :) - q_ref(j, :))^2 + ...
                    2 * (q_ref(i, :) - q_ref(j, :)) * (q_new(i, :) - q_new(j, :))' >= params.d_min^2;
            end
        end
        
        % Constraint (29): Maximum rate constraint
        for k = 1:K
            for m = 1:M
                % Reference point distance and elevation angle ζ_{km} and ζ_{km}^r
                distance_ref = norm(q_ref(m, :) - params.w_k(k, :));
                
                % Calculate elevation angle (ensure positivity)
                zeta_ref = atan(uav_heights(m) / distance_ref) * (180 / pi); % Angle in degrees
                
                % Calculate X_{km}^r
                X_km_ref = 1 + exp(-(params.Ba + params.Bb * zeta_ref));
                
                % Calculate Y^r_km (distance squared + UAV height squared)
                Y_r_km = distance_ref^2 + uav_heights(m)^2;
                
                % Calculate Γ_{km}^r
                Gamma_km_ref = (params.Bc + (params.Bd / X_km_ref)) * ...
                    log2(1 + (params.gamma_0 / (Y_r_km^(params.alpha_L / 2))));
                
                % Calculate Ω_{km}^r
                Omega_km_ref = (params.Bd * log2(exp(1))) / (X_km_ref^2) * ...
                    log(1 + (params.gamma_0 / (Y_r_km^(params.alpha_L / 2))));
                
                % Calculate Ψ_{km}^r
                Psi_km_ref = (params.Bc + params.Bd / X_km_ref) * ...
                    (params.gamma_0 * (params.alpha_L / 2) * log2(exp(1))) / ...
                    (Y_r_km * ((Y_r_km^(params.alpha_L / 2)) + params.gamma_0));
                Psi_km_ref = max(Psi_km_ref, epsilon); % Avoid Psi being zero or numerical errors
                                
                % Compute exp(...) difference
                exp_diff = exp(-(params.Ba + params.Bb * zeta_new(k, m))) - ...
                    exp(-(params.Ba + params.Bb * zeta_ref));
                
                % Compute norm difference using square_pos
                norm_diff = (q_new(m, 1) - params.w_k(k, 1))^2 + (q_new(m, 2) - params.w_k(k, 2))^2 - ...
                    norm(q_ref(m, :) - params.w_k(k, :))^2;
                
                % Combined R_{km}^{lb}
                inv_pos(tau_u(k, m)) <= (Gamma_km_ref - Omega_km_ref * exp_diff - Psi_km_ref * norm_diff);
            end
        end

        % Constraint (28): Total transmission time bounded by slack variable R
        for k = 1:K
            for m = 1:M
                inner_sum = 0; % Initialize inner summation
                for n = 1:N
                    for l = 1:L
                        % Compute Z_kmnl
                        Z_kmnl_val = 0.5 * (x_new(m, n, l) + tau_u(k, m))^2 - ...
                            0.5 * (x_ref(m, n, l)^2 + tau_ref(k, m)^2) - ...
                            x_ref(m, n, l)*(x_new(m, n, l) - x_ref(m, n, l)) - ...
                            tau_ref(k, m)*(tau_u(k, m) - tau_ref(k, m));
                        adjusted_val = Z_kmnl_val + (1 - x_new(m, n, l)) * params.tau_bk(k);
                        
                        % Add weighted layer summation
                        layer_sum = sum(params.o(n, 1:l) * adjusted_val);
                        inner_sum = inner_sum + params.lambda(k, n, l) * layer_sum;
                    end
                end
                total_sum = total_sum + a(k, m) * inner_sum;
            end
        end
        total_sum <= R;

        % Constraint (3): Cache capacity constraint
        for m = 1:M
            sum(sum(params.o .* squeeze(x_new(m, :, :)))) <= params.C_max;
        end
        
        % Constraint (17): Caching strategy bounds
        for m = 1:M
            for n = 1:N
                for l = 1:L
                    0 <= x_new(m, n, l) <= 1;
                end
            end
        end

    cvx_end
    cvx_clear

    % Update local points
    x_ref = x_new;
    q_ref = q_new;
    tau_ref = tau_u;
    params.xi = params.xi * 1.2;

end

I think the problem might be because of :

1. Psi_km_ref * exp_diff is too small, since I get Psi_km_ref = 3.6339e-12
   the solver can run if i do Psi_km_ref = max(Psi_km_ref, epsilon);
   but the value of output is kinda wrong i think…
   (The delay of 1 bit will become large as 1 ~ 100…

2. maybe i should not put Zeta_new ζ as a variable?

3. the expression of total_sum & total_sum <= R

I can give the paper I’m trying to redo if that helps.
If anyone can help, it’s much appreciated Thank you a lot!

( I’m now trying to scale down the Psi_km_ref , but i don’t really sure that it’s the main reason that occurs the problem
eg. 1.slow bit rate per sec τ

2. cache deployment x(a,b,c) should act like x(a,b,c)=1 if x(a,b,c+1)=1
   instead of x(a,b,c)=0 and x(a,b,c+1)=1

[Mark_L_Stone]

Two different but related things:

Scaling in initial optimization problem provided to CVX. Try to avoid very large and very small numerical values. So improve that.

Scaling may get worse in subsequent SCA iterations. Even if scaling was good in first iteration, things can get wilder and wilder in these subsequent SCA iterations.

Starting value used in SCA might have a major impact on its evolution. Any little difference from what and how was run in the paper could cause very different outcome of SCA. You don’t know every little detail of what was done in the paper, unless they provided reproducible code for everything, including specification of computer environment, solver and tool versions and settings, etc., and of course starting values,

The result obtained using the SeDuMi solver is inaccurate. The optimal solution is not as good as before the optimization.

Unsafeguarded (no line search or trust region)Successive Convex Approximation (SCA) or generally, alternating variables optimization are unreliable. It might not descend (for minimization problem), i.e., iterates could get worse. It might not converge to anything; and if it does converge, it might not be to a local optimum of the original problem, let alone a global optimum. The solution of successive iterations, and therefore subproblem inputs, can become wilder and wilder, until at some point …

[Allenyang (淙珺 楊)]

I really want to solve the problem but i couldn’t find a correct way to scale it : (
they do provided many parameters including the environment Matlab R2021b tools and CVX with solver SDPT3
Should i try Mosek or is there a better way to re-scale it
I can’t rlly figure out a good way to solve this… it bothers me so much :'8
what method will ppl like u try ,you seem so professional

[Mark_L_Stone]

Perhaps the people for whom SCA works well don’t post because they don’t need help. But most people posting on this forum about SCA encounter major difficulties

In any event, my advice stands. SCA is very precarious as I wrote in the link. Your best hope might be to contact the authors of the paper for additional details on what they did, including code and starting values.

[Allenyang (淙珺 楊)]

Thank you for the reply man !
I’ll try to contact the authors for help , Wish you a good day

[Mark_L_Stone]

And of course, if your input data is not EXACTLY the same as what was run for the paper, then all bets are off, even if you use identical code and software (other than input data).

I will not impugn the authors of whatever paper you are dealing with. But I suspect that for some papers dealing with SCA, even in reputable journals, the authors might have had to do a lot of experimentation to find an example which works, and then only report the successes, but not the more numerous failures. Then readers are surprised when they can’t get the algorithm to work.

[Allenyang (淙珺 楊)]

I’m sorry to bother you, but I have a small question.
Could there be any issues with my constraints?
I’ve reviewed them numerous times, but I still can’t figure out the problem.
Perhaps there are some issues that I could address or correct?

[Mark_L_Stone]

It’s “your” model, so I can’t say whether the constraints are correct. But you don’t have any kind of trust region constraints added for SCA, so anything can happen. My views on the perils of SCA have not changed since yesterday.