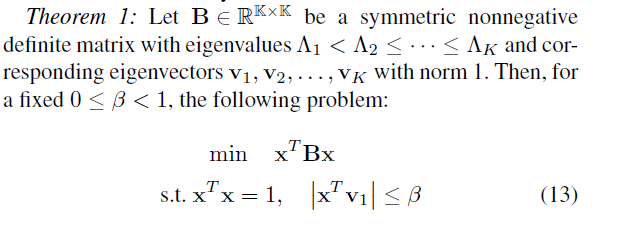
Absolute function is convex? and 2^x can use cvx?

1

  1. i have wonder ,if x is a variable vector ,v1is constant vector,absolute | x^T*v1| is cnvex?
  2. x is a variable vector,2^x can use cvx?
2
  1. help cvx/abs
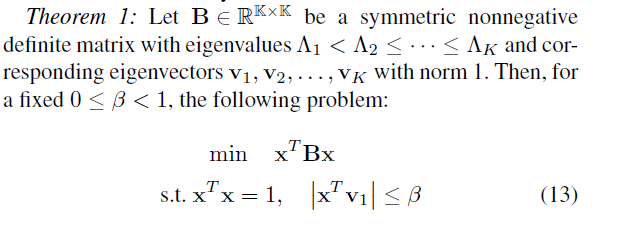
 Disciplined convex/geometric programming information for abs:
    abs(X) is convex and nonmonotonic in X. Therefore, according to
    the strict rules of DCP, X must be affine. However, because of
    its special structure, CVX considers the sign of X as well. So,
    for instance, if X is known to be nonnegative, then abs(X)=X.

x' * v1 is affine (as a function of x) if v1 is constant. Therefore, abs(x’ * v1) is convex and is formed in accordance with CVX’s rules, and therefore
abs(x' * v1) <= beta
will be accepted by CVX.

  1. 2^x can be re-written as exp(x*log(2)) , which will be accepted by CVX. CVX is smart enough to apparently do this transformation and accept 2^x directly, although I don’t see the rule in the CVX Users’ Guide which says that it will do so. I will let @mcg either acknowledge the opportunity to add such mention to the Users’ Guide or point out which rule therein covers this.
3

Thank you very much for your help, i have wonder,for 2^x ,could i re-written as power(2,x) in cvx ?

4

Yes, you are right. There are two forms of power. The first form has the first argument be a CVX expression and the second argument a constant. The second form has the first argument be a constant and the second argument a CVX expression. This second form is documented as follows in the CVX Users’ Guide.

power(p,x) p.^x and p^x, where p is a real constant and x is a real variable. For p^x, both p and x
must be scalars. Valid values of p include:
• p element of {0,1} Constant.
• 0 < p < 1. Convex and nonincreasing; x must be concave.
• p > 1. Convex and nondecreasing; x must be convex.
Negative values of p are not permitted.

That CVX will directly accept p^x, rather than requiring use of power(p,x), appears to be undocumented (or at least I can’t find it).

5

you are so kind ,thank you

6

Well, the formatting may be improvable but you quoted the very section that says you can use p^x and p.^x directly…